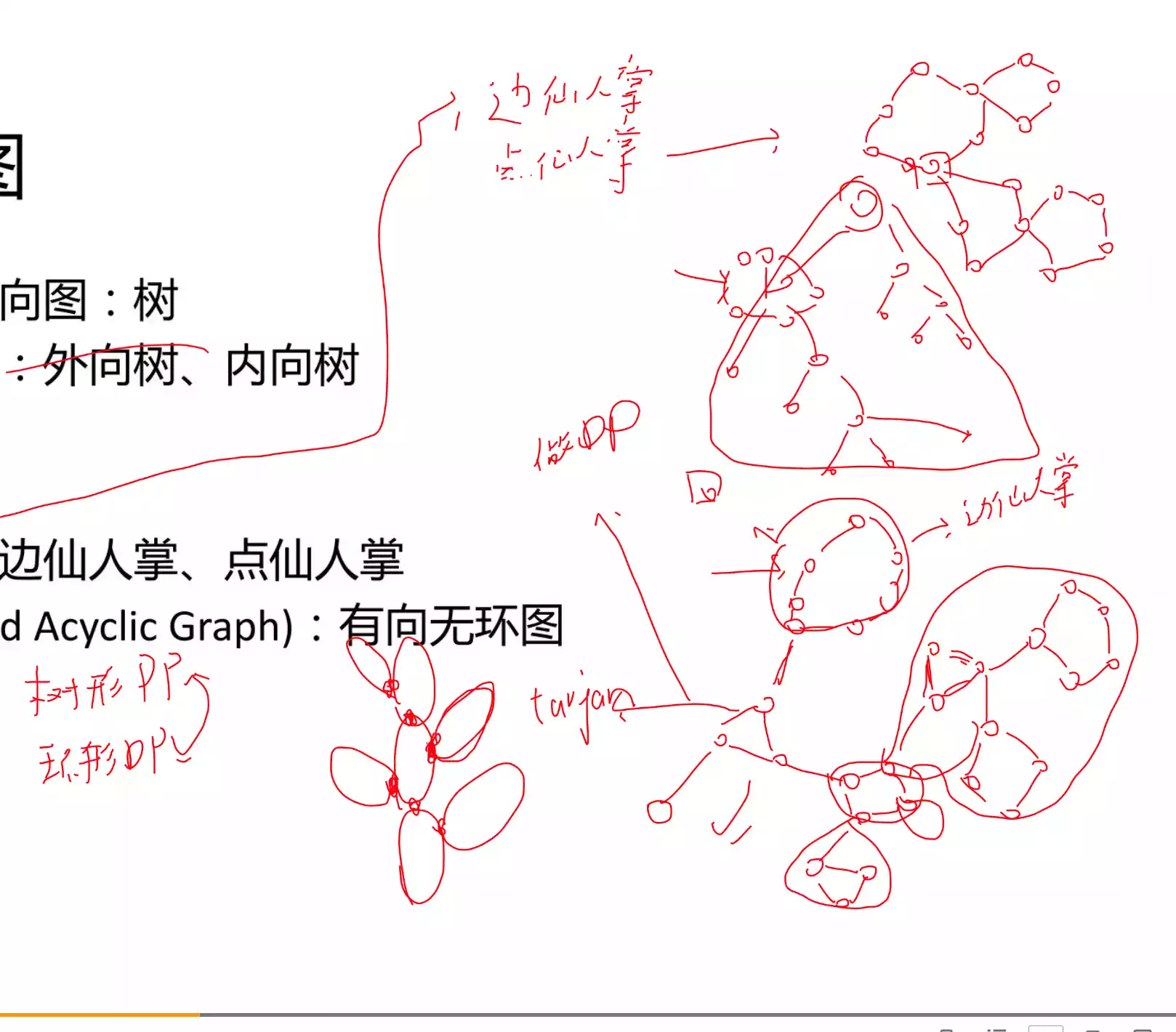
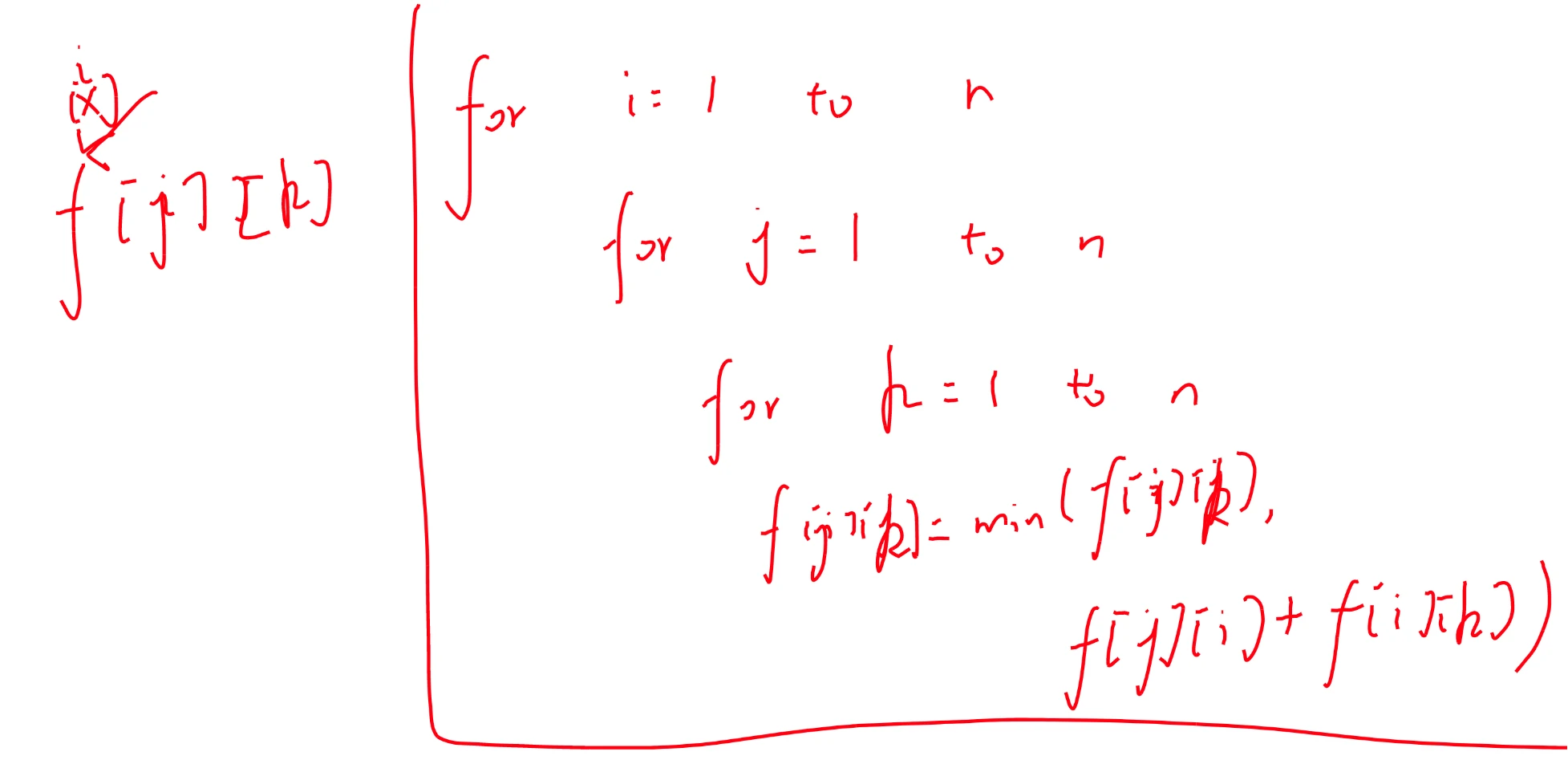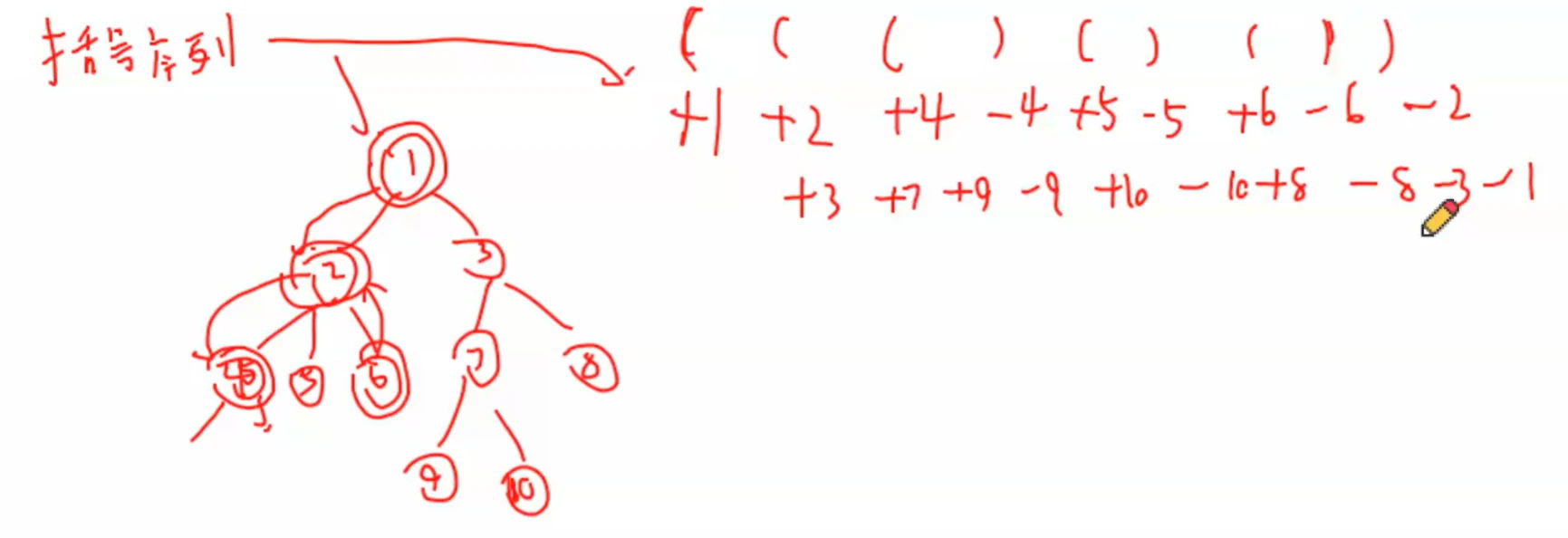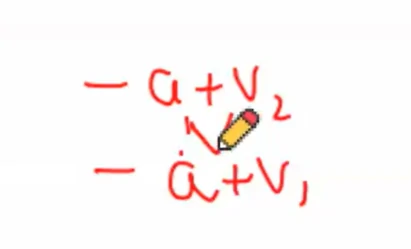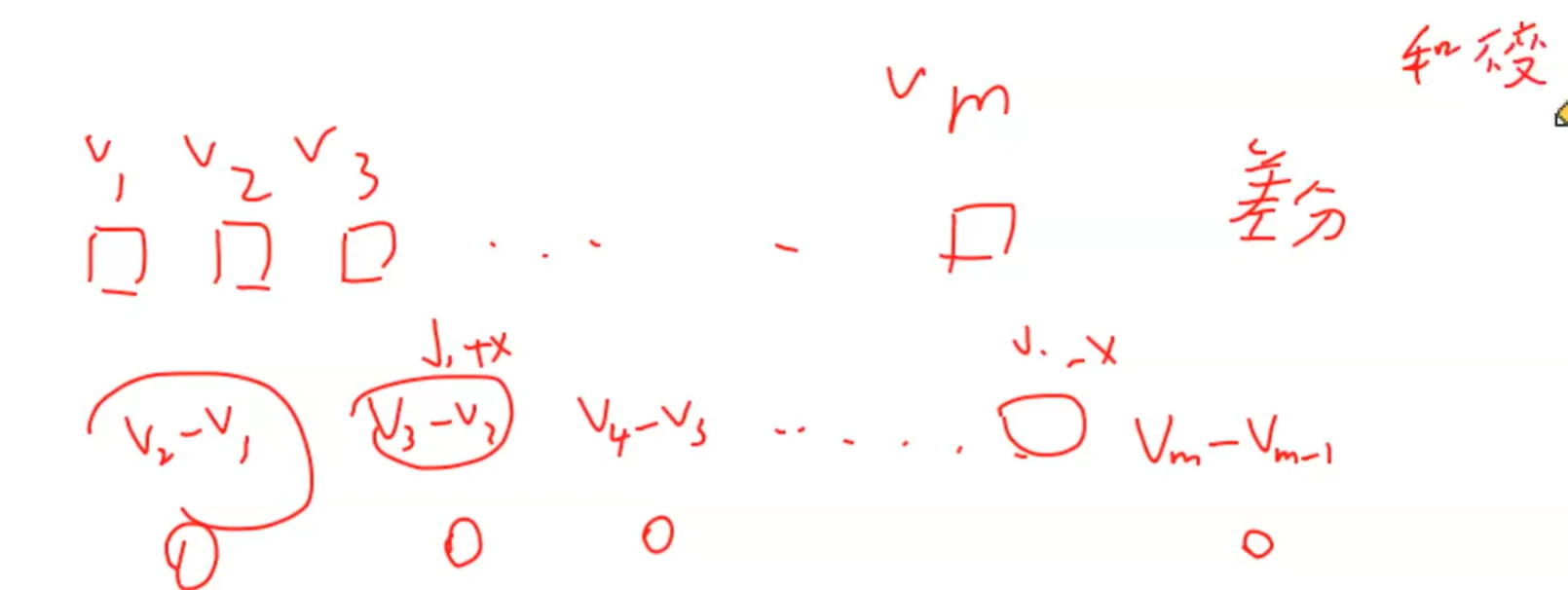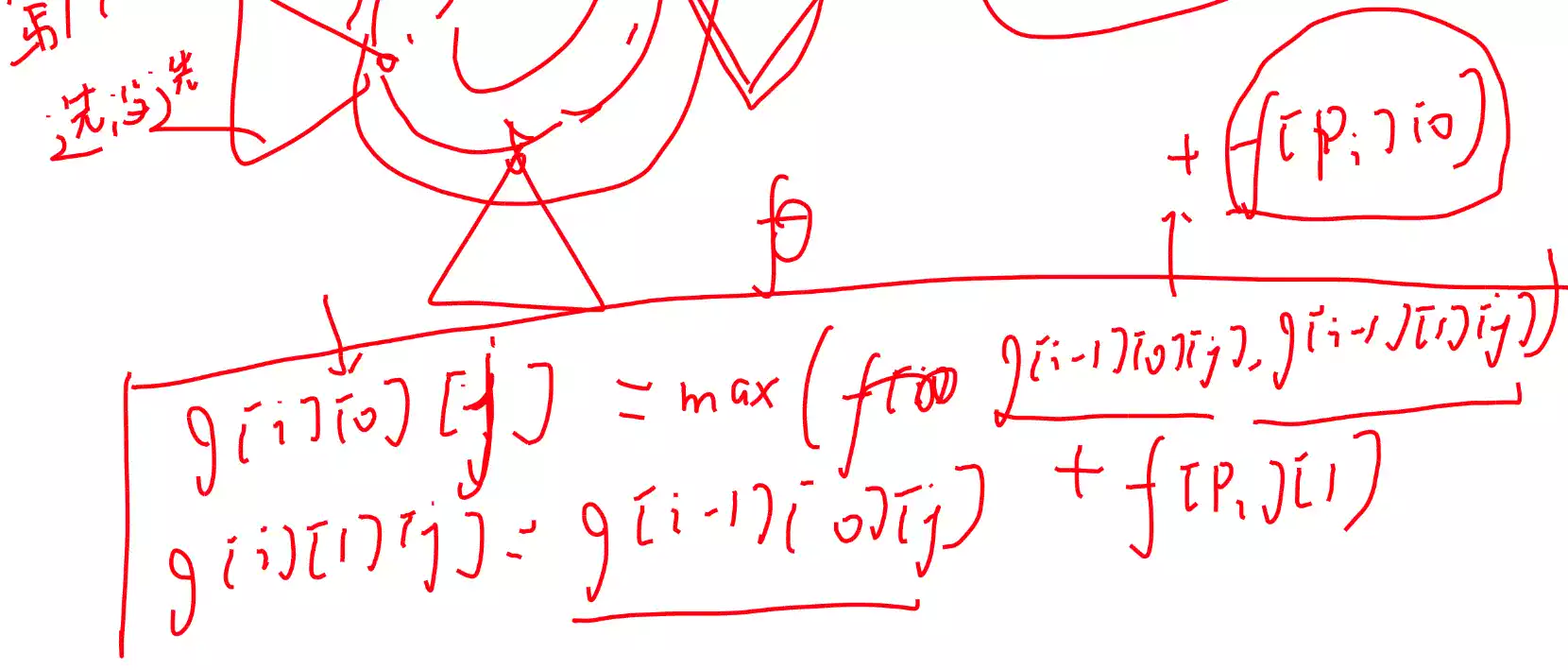度(Degree):一个顶点上的度是指与该顶点相关联的边的条数,顶点v v v d ( v ) d(v) d ( v ) 入度(In-degree)和出度(Out-degree):对于有向图来说,一个顶点的度可细分为入度和出度。顶点的入度是指与其关联的各边之中,以其为终点的边数;出度则是相对的概念,指以该顶点为起点的边数。 自环(Loop):若一条边的两个顶点为同一个顶点,则此边称之为自环。 路径(Path):在图上随便走,走出来的就是路径。 环:起点=终点的路径。 简单路径:每个点至多走一次的路径(点不能重复,边可以)。 简单环:去掉起点终点后变成简单路径(起点终点可以走两遍)。 完全图:所有点之间都有边。该图有n n n n × ( n − 1 ) 2 \dfrac{n\times(n-1)}{2} 2 n × ( n − 1 ) 无向图总度数一定是偶数,因为从什么都没有开始每次加一条边,就有两个点的度数加一。
如何找环呢?
从根节点开始 DFS,
直到从某一个点走到了它的祖先,
如果 DFS 途中找到了这个点的祖先,
那么就反向跳不断地跳到他的父亲,
直到找到这个点,
那么经历的所有点便组成了一个环。
树是二分图 。
只需要把深度为奇数的点放在左边,
深度为偶数的点放在右边(没有上司的舞会),
那么边一定全在中间。
什么图不是二分图呢?
有奇环的图就一定不是,没有奇环就是(环上的点数是奇数),
代码思路:随便找到一个点把它染成白色,再染相邻的点。
何时结束?
染完以后发现相邻有与自己颜色相同的点,那么就不是二分图。
二分图不一定连通。
f [ i ] [ j ] f[i] [j] f [ i ] [ j ] i i i j j j
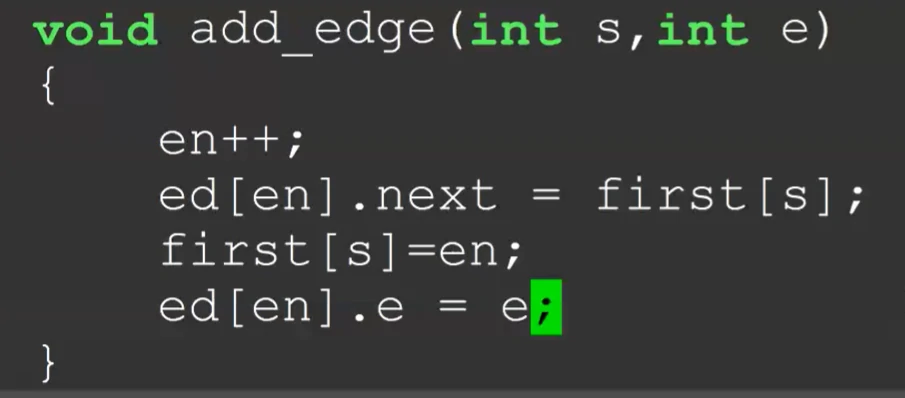
好处:询问快,好写。 坏处:空间较大,没有办法处理重边。 既然会存图了,那么我们做一下章鱼图DP吧!
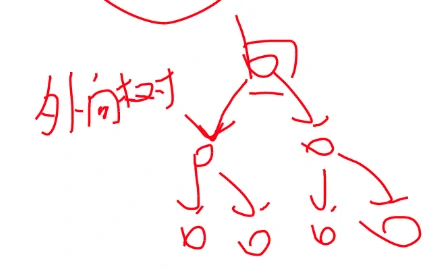
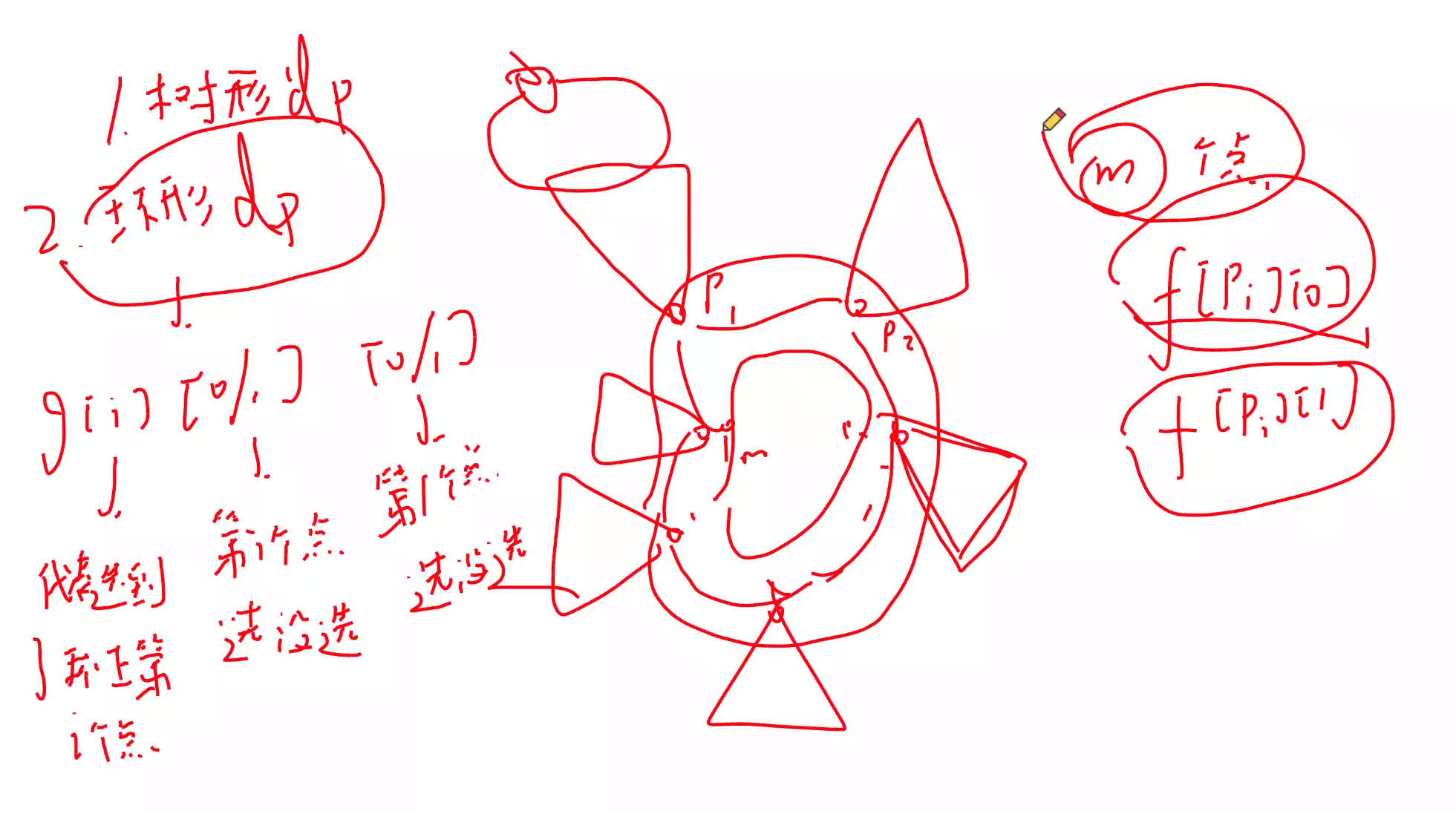
对环上的每一个点做一个 树形DP
保证不要 DFS 到环上
做完 树形DP 后再对环做一个 环形DP 那么就做完了
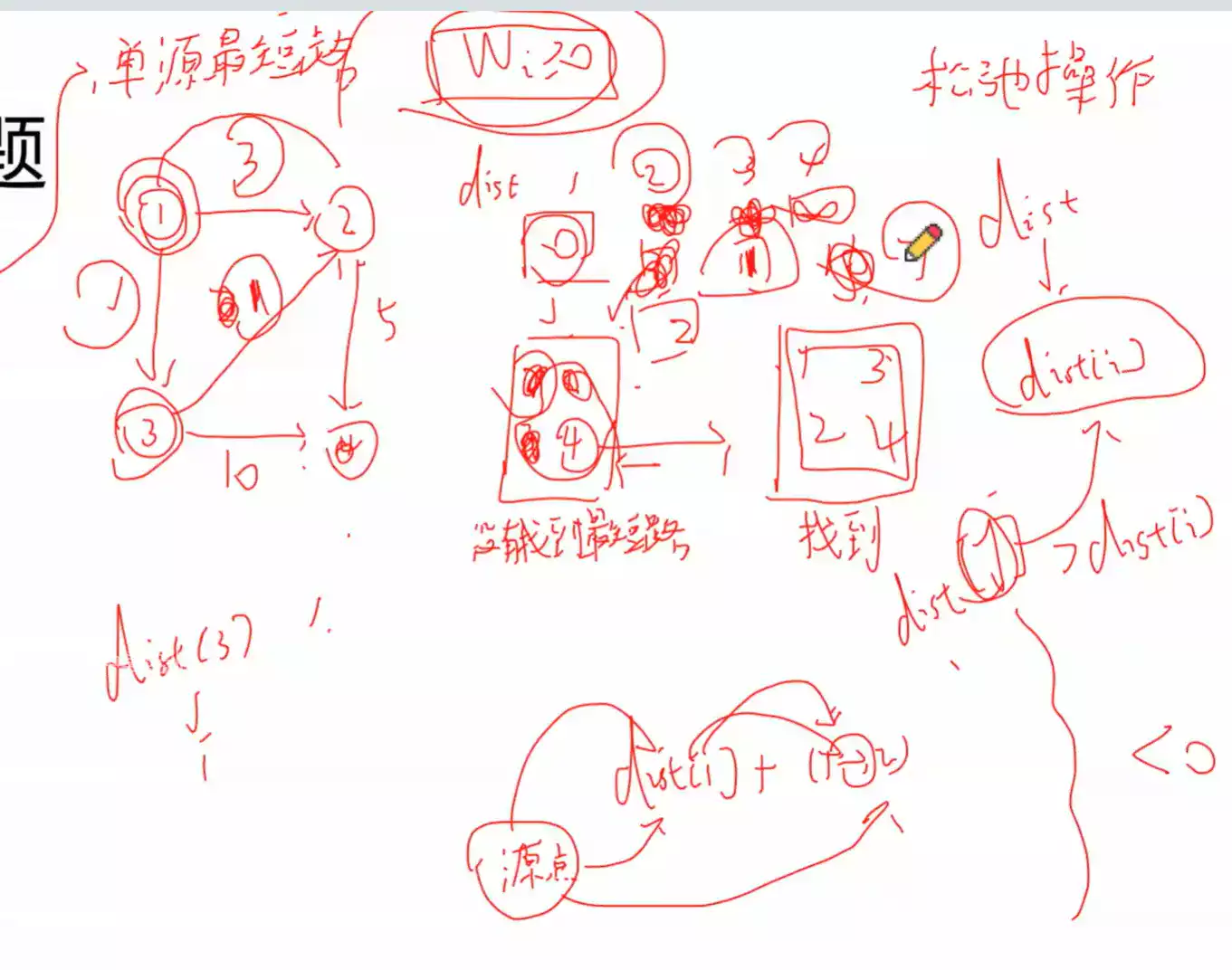
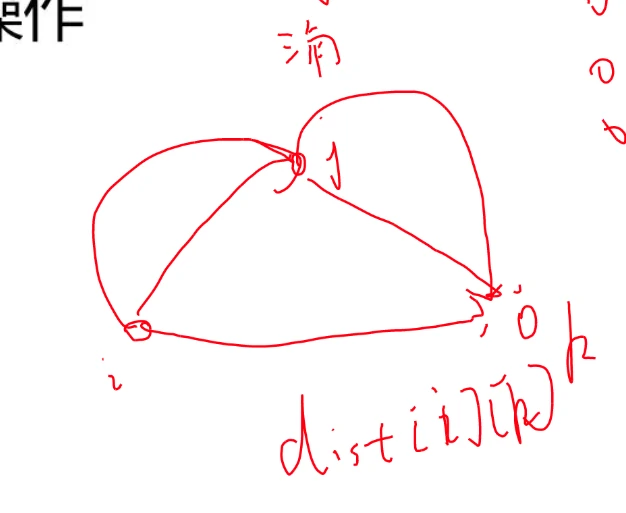
单源最短路(一个点到其他所有点)三角不等式( d i s t i , k < = d i s t i , j + d i s t j , k ) (dist i,k <= dist i,j+dist j,k) ( d i s t i , k < = d i s t i , j + d i s t j , k ) 多源最短路(多个点到所有点的最短路——多次单源最短路 ) 条件 :边权大于等于0 。
F i , j , k F i,j,k F i , j , k j j j k k k i i i
现在又加了一条边。
这条边可选可不选。
但是i i i
进行一个状态压缩 。
注意要先枚举中间点。
首先,i i i j j j n − 1 n-1 n − 1
每次循环枚举所有的边来进行松弛操作,后面的边会被前面的边更新。
即使最差的顺序,倒着遍历,导致每次只能更新一条边,那最多也不会超过 n − 1 n-1 n − 1
所以就得到了如下代码,
是不是肥肠简单捏。
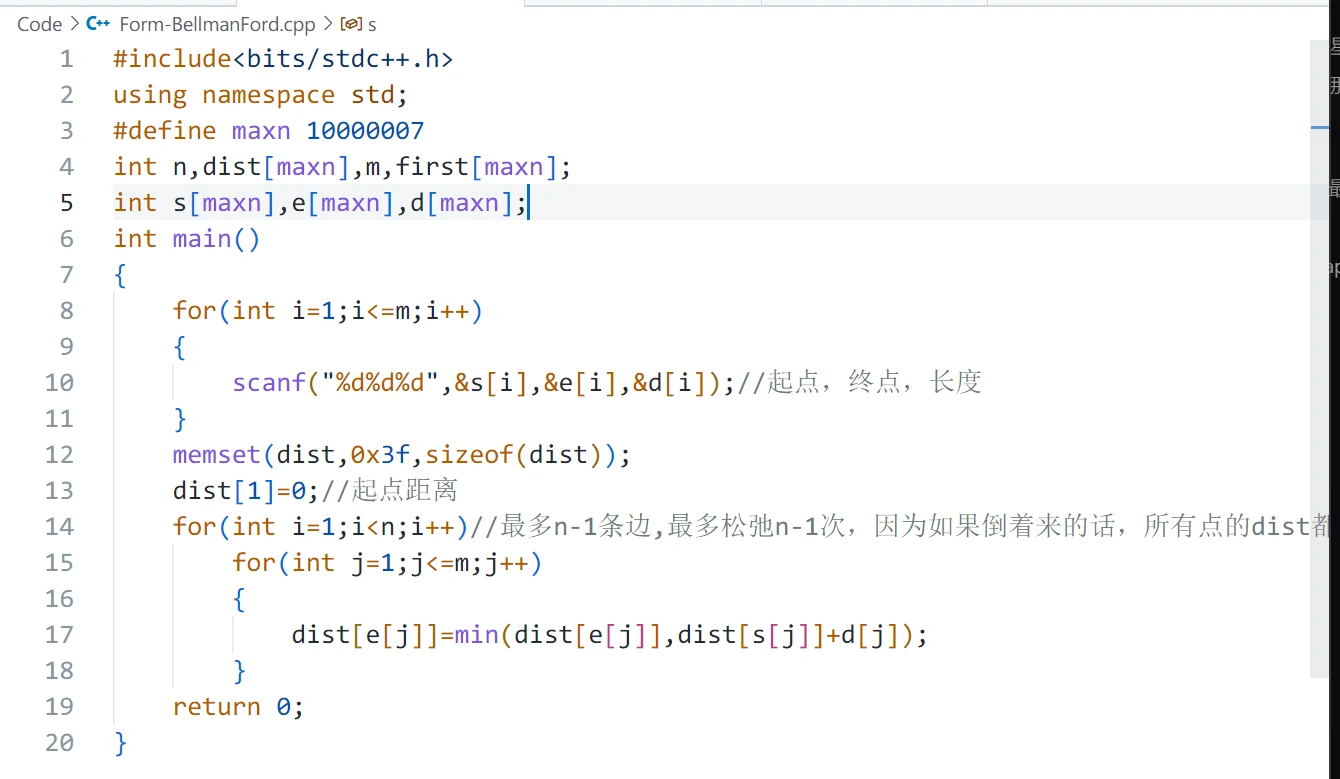
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> using namespace std;#define maxn 10000007 int n,dist[maxn],m,first[maxn];int s[maxn],e[maxn],d[maxn];int main () for (int i=1 ;i<=m;i++) { scanf ("%d%d%d" ,&s[i],&e[i],&d[i]); } memset (dist,0x3f ,sizeof (dist)); dist[1 ]=0 ; for (int i=1 ;i<n;i++) for (int j=1 ;j<=m;j++) { dist[e[j]]=min (dist[e[j]],dist[s[j]]+d[j]); } return 0 ; }
但是复杂度比 Dijkstra 高。
但是它能处理负边权和负环,因为它每一条边都会看n − 1 n-1 n − 1
如果进行 n − 1 n-1 n − 1 n n n
因为假如一张图所有的点的最短路都被求了出来,并且其中不存在负环,这时遍历每一条边进行松弛操作,我们会发现什么也不会发生。
若仅仅出现了负边权,其实也什么都不会发生。
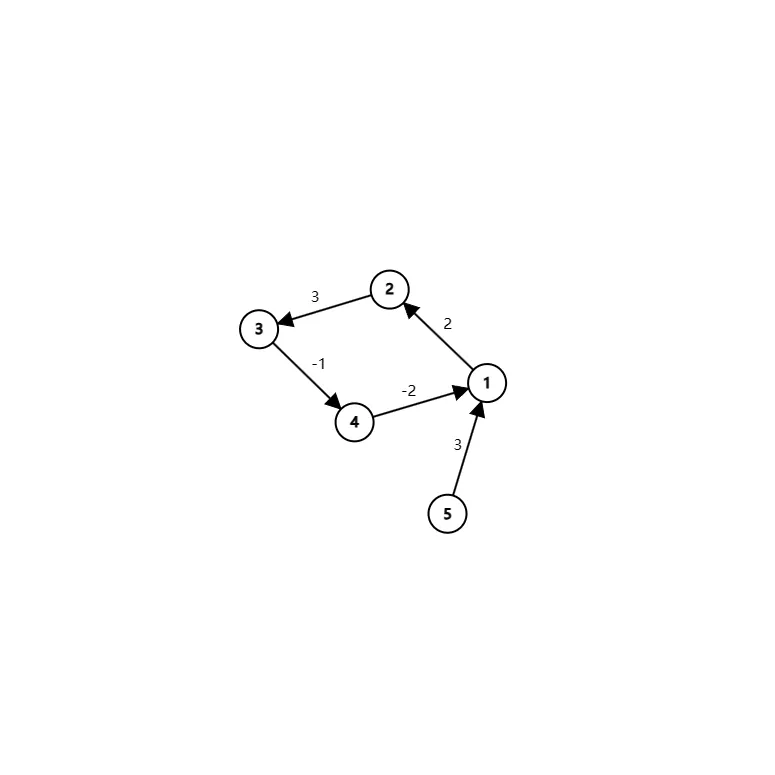
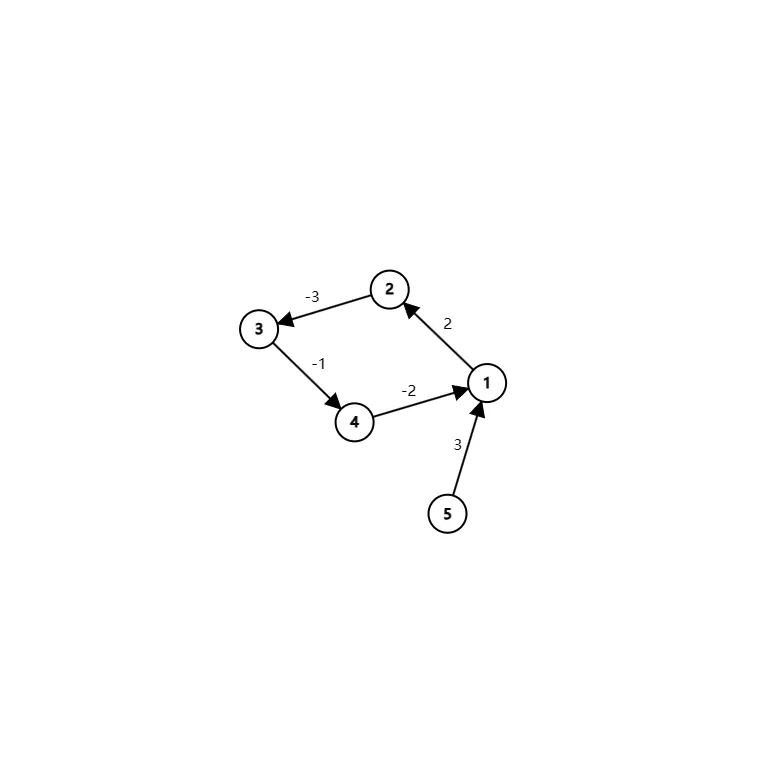
举个例子:
对于这样一张图,进入环以后会发现:每条边被松弛一遍后,每个点的 d i s t dist d i s t
而对于这样一张有负环的图,当遍历回原点这条边时,会发现它的d i s t dist d i s t
根据负环的定义:边权和为负数的环 。我们可以知道,其实关键就是在于从进入环到回到起点的那一刻,起点的d i s t dist d i s t
导致了负环连出去的点最短路径都是负无穷。
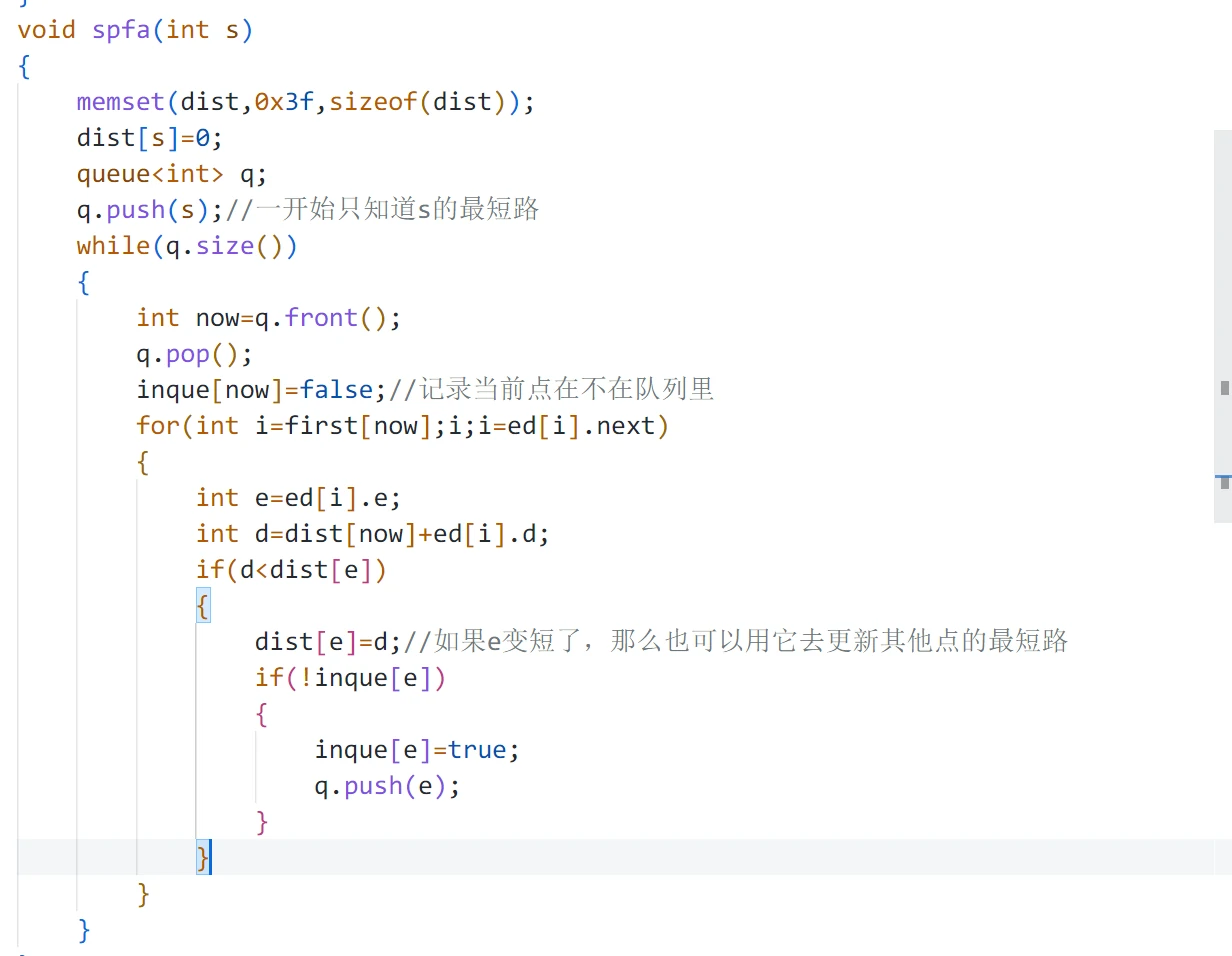
关于SPFA ,它死了。
和 BFS 不一样的地方就是一个点可能被扔进队列多次,
实际上就是 Bellman-Ford 的队列优化,
复杂度O ( n m ) O(nm) O ( n m ) O ( m ) O(m) O ( m )
如果边权大于等于零,一定是用 Dijkstra+ + +
如果小于零那就是 SPFA 。
在松弛操作的时候,假如这条边的终点没被标记,假如终点的dist值比队头要大,那就放在队尾,如果比队头小,那就加在队头。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 for (int i=fir[now];i;i=ed[i].nxt) { int v=ed[i].to; if (dist[v]>dist[now]+ed[i].val) { dist[v]=dist[now]+ed[i].val; if (!righ[v]) { righ[v]=true ; if (!q.empty ()&&dist[q.front ()]<dist[v]) q.push_back (v); else q.push_front (v); } } }
图上边权大于等于0 。
复杂度 O ( n 2 + m ) O(n^2+m) O ( n 2 + m )
记d i s t i dist_i d i s t i i i i
1 1 1 0 0 0
其他点为无穷大。
把一号点放到右边,
进行一个松弛操作,
“用已知更新未知”。
用已知最短路的点更新未知最短路的点。
用dist最短的点 去更新其他点,
更新过最短距离的点不会被再次更新
因为边权大于等于0 0 0
假如j j j i i i
并且d i s t [ i ] dist[i] d i s t [ i ] d i s t [ j ] dist[j] d i s t [ j ]
j j j d i s t [ i ] dist[i] d i s t [ i ]
因此d i s t [ i ] dist[i] d i s t [ i ]
1.询问最小值。
2.删除最小值。
3.修改某些值。
大根堆:仿函数 greater<int>
用 pair 的话默认是按照 first 排序,其次按照 second 排序。
可以使用堆/线段树。
代码:
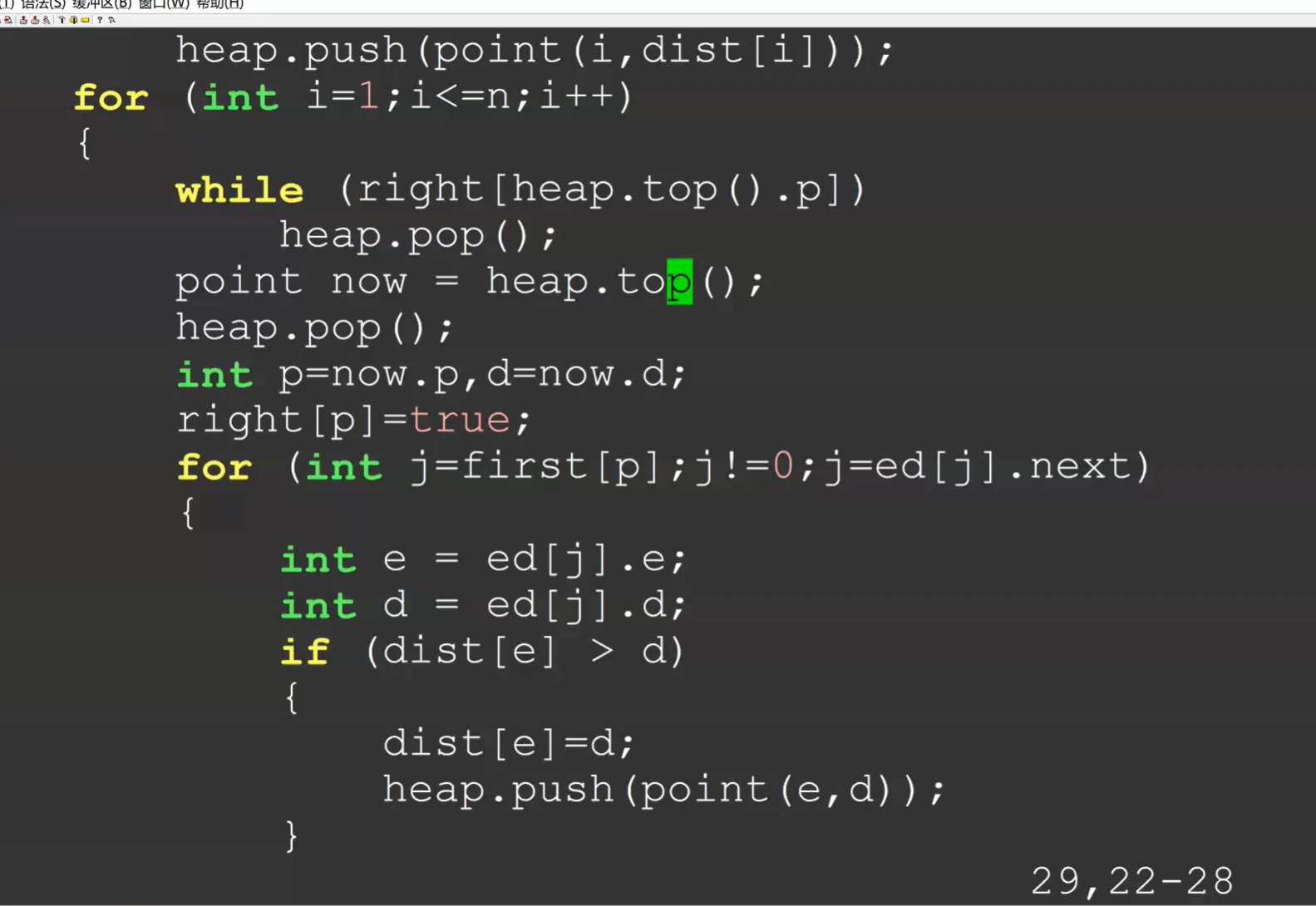
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 #include <bits/stdc++.h> using namespace std;#define maxn 1000007 int dist[maxn],first[maxn];int n,m,s;bool righ[maxn];struct point { int p,d; point (){} point (int a,int b){p=a;d=b;} }; bool operator <(const point &a,const point &b){ return a.d>b.d; } priority_queue<point> heap; struct edge { int e,next; int d; }ed[maxn]; int cnt;void add_edge (int u,int v,int w) cnt++; ed[cnt].next=first[u]; ed[cnt].e=v; ed[cnt].d=w; first[u]=cnt; } void dijkstra (int s) memset (dist,0x3f ,sizeof (dist)); dist[s]=0 ; for (int i=1 ;i<=n;i++) heap.push (point (i,dist[i])); for (int i=1 ;i<=n;i++) { while (righ[heap.top ().p]) heap.pop (); point now=heap.top (); heap.pop (); int p=now.p; righ[p]=1 ; for (int j=first[p];j; j=ed[j].next) { int e=ed[j].e; int d=dist[p]+ed[j].d; if (dist[e]>d) { dist[e]=d; heap.push (point (e,d)); } } } } signed main () scanf ("%d%d%d" ,&n,&m,&s); for (int i=1 ;i<=m;i++) { int u,v,w; scanf ("%d%d%d" ,&u,&v,&w); add_edge (u,v,w); } dijkstra (s); for (int i=1 ;i<=n;i++) { if (dist[i]==1061109567 ) { cout<<2147483647 <<" " ; continue ; } printf ("%d " ,dist[i]); } return 0 ; }
由于 Dijkstra 采用的是贪心策略,每个点只被加入堆中一次,这样的话一旦出现负环,那么明明可以绕很多圈让路径长度变为负无穷,但是 Dijkstra 只会跑一遍,导致贪心最优得出答案错误。
负边权也是同理,假如当前最小的d i s t dist d i s t d i s t dist d i s t
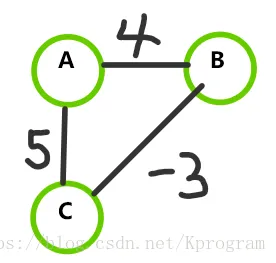
例如该图,求 A 到 B 的最短路。
最小距离为2,但是 Djkstra 会认为是4。
堆的做法(优先队列):
( n + m ) × l o g ( n + m ) (n+m) \times log(n+m) ( n + m ) × l o g ( n + m )
手写堆:$$(n+m)\times log_n$$(斐波那契堆会更快)
一种多源最短路算法
新建一个虚拟节点零号点,把它向其它所有点连接一条边权为 0 的边,
然后用 Bellman-Ford 求出 0 号点到其它所有点的最短路,记为 h i h_i h i
设存在一条从 u u u v v v w w w w + h u − h v w+h_u-h_v w + h u − h v n n n
如果不这样处理,将会导致负边权。
在新图上跑 Dijkstra 后,对于 u → v u\to{v} u → v + h s − h t +\,h_s-h_t + h s − h t − h s + h t -h_s+h_t − h s + h t
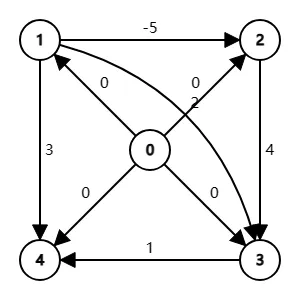
原图:
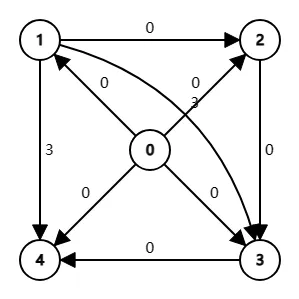
新图:
一开始的预处理,到超级源点的最短距离要么就是零,要么就是负数,所以不需要初始数组为极大值。
但是如果是SPFA的话,需要判断是否有更新过,不然不会入队,所以还是要标记初始为极大值。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 #include <bits/stdc++.h> using namespace std;typedef long long ll;const int N = 1e4 + 10 ;const int M = 6e3 + 10 ;int n, m, edcnt;int h[N];int s[N],t[N],d[N];int fir[N];int dist[N];bool vis[N];struct edge { int to, val, nxt; }e[(M << 1 ) + N]; struct point { int id,len; point (){} point (int a,int b):id (a),len (b){} bool operator < (const point &x)const { return len > x.len; } }; void Add (int u, int v, int w) e[++edcnt].nxt = fir[u]; e[edcnt].to = v; e[edcnt].val = w; fir[u] = edcnt; } void Dijkstra (int s) memset (dist, 0x3f , sizeof (dist)); memset (vis, 0 , sizeof (vis)); dist[s] = 0 ; priority_queue<point> q; while (!q.empty ()) q.pop (); q.push (point (s,0 )); while (!q.empty ()) { point now = q.top (); q.pop (); if (vis[now.id]) continue ; vis[now.id] = true ; for (int i = fir[now.id]; i; i = e[i].nxt) { int v = e[i].to; int d = dist[now.id] + e[i].val; if (d < dist[v]) { dist[v] = d; if (!vis[v]) q.push (point (v,dist[v])); } } } } int main () scanf ("%d%d" ,&n,&m); for (int i = 1 ; i <= m; ++i) scanf ("%d%d%d" ,&s[i],&t[i],&d[i]); int tot = m; for (int i = 1 ; i <= n; ++i) { s[++tot] = 0 ; t[tot] = i; d[tot] = 0 ; } for (int i = 1 ; i <= n; ++i) for (int j = 1 ; j <= n + m; ++j) h[t[j]] = min (h[t[j]], h[s[j]] + d[j]); for (int j = 1 ; j <= n + m; ++j) if (h[t[j]] > h[s[j]] + d[j]) { printf ("-1" ); return 0 ; } for (int i = 1 ; i <= m; ++i) Add (s[i], t[i], d[i] + h[s[i]] - h[t[i]]); for (int i = 1 ; i <= n; ++i) { Dijkstra (i); ll ans = 0 ; for (int j = 1 ; j <= n; ++j) ans += j * (dist[j] == 0x3f3f3f3f ? 1e9 : dist[j] - h[i] + h[j]); printf ("%lld\n" , ans); } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 #include <bits/stdc++.h> using namespace std;typedef long long ll;const int N = 1e4 + 10 ;const int M = 6e3 + 10 ;int n, m, edcnt;int h[N];int fir[N];int dist[N];bool vis[N];struct edge { int to, val, nxt, from; }e[(M << 1 ) + N]; struct point { int id,len; point (){} point (int a,int b):id (a),len (b){} bool operator < (const point &x)const { return len > x.len; } }; void Add (int u, int v, int w) e[++edcnt].nxt = fir[u]; e[edcnt].from = u; e[edcnt].to = v; e[edcnt].val = w; fir[u] = edcnt; } bool SPFA (int s) bool inque[N]; int times[N]; memset (times, 0 , sizeof (times)); memset (inque, 0 , sizeof (inque)); memset (h, 0x3f , sizeof (h)); queue<int > q; times[s] = 1 ; h[s] = 0 ; q.push (s); while (!q.empty ()) { int now = q.front (); q.pop (); inque[now] = false ; for (int i = fir[now]; i; i = e[i].nxt) { int v = e[i].to; int d = h[now] + e[i].val; if (d < h[v]) { h[v] = d; if (!inque[v]) { inque[v] = true ; q.push (v); times[v]++; if (times[v] > n) return false ; } } } } return true ; } void Dijkstra (int s) memset (dist, 0x3f , sizeof (dist)); memset (vis, 0 , sizeof (vis)); dist[s] = 0 ; priority_queue<point> q; while (!q.empty ()) q.pop (); q.push (point (s,0 )); while (!q.empty ()) { point now = q.top (); q.pop (); if (vis[now.id]) continue ; vis[now.id] = true ; for (int i = fir[now.id]; i; i = e[i].nxt) { int v = e[i].to; int d = dist[now.id] + e[i].val; if (d < dist[v]) { dist[v] = d; if (!vis[v]) q.push (point (v,dist[v])); } } } } int main () scanf ("%d%d" , &n, &m); for (int i = 1 ; i <= m; ++i) { int u, v, w; scanf ("%d%d%d" , &u, &v, &w); Add (u, v, w); } for (int i = 1 ; i <= n; ++i) Add (0 , i, 0 ); if (!SPFA (0 )) { printf ("-1" ); return 0 ; } for (int i = 1 ; i <= m; ++i) e[i].val += h[e[i].from] - h[e[i].to]; for (int i = 1 ; i <= n; ++i) { Dijkstra (i); ll ans = 0 ; for (int j = 1 ; j <= n; ++j) ans += j * (dist[j] == 0x3f3f3f3f ? 1e9 : dist[j] - h[i] + h[j]); printf ("%lld\n" , ans); } return 0 ; }
整个环权值的和为负
做 SPFA 时候可以多记一个c n t i cnt_i c n t i n − 1 n-1 n − 1 如果一个点入队超过n − 1 n-1 n − 1 ≤ \le ≤
对应最短路中的 d < = d i s t [ i ] + w [ i ] d <= dist [i]+w[i] d < = d i s t [ i ] + w [ i ]
最大值对应最短路
解释:
对于每一个 a i a_i a i a i a_i a i a j a_j a j ⩽ \leqslant ⩽ k i k_i k i
也就是a i a_i a i ⩽ \leqslant ⩽ a j a_j a j k i k_i k i
这不就是最短路中的松弛操作嘛!
要使这些条件都满足
式子上下相加
那么一定是对每一个不等式的右面之和取一个m i n min m i n
也就是求一个最小值 最短路
那么同理
最小值对应最长路
例子:对于树上的一些路径进行访问,问一条路径上的点被访问的次数。
每次有一个 s , t s,t s , t
1 2 3 4 d[s]++; d[t]++; d[lca]--; d[fa[lca]]--;
这样访问值的时候,访问以该节点为根的子树和即可。
而假如对边差分,可以把边权对应到较深的点上,然后就可以得到一下操作:
1 2 3 d[s]++; d[t]++; d[lca] -= 2 ;
P3128
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 #include <bits/stdc++.h> using namespace std;const int N = 5e4 + 10 ;int n, k, ans;int cf[N];int dep[N];int fir[N];int st[N][25 ];struct Edge { int nxt, to; }e[N << 1 ]; int cnt;void add (int u, int v) e[++cnt].to = v; e[cnt].nxt = fir[u]; fir[u] = cnt; } void dfs1 (int u, int fa) for (int i = fir[u]; i; i = e[i].nxt) { int v = e[i].to; if (v == fa) continue ; st[v][0 ] = u; dep[v] = dep[u] + 1 ; for (int j = 1 ; j <= 23 ; j++) st[v][j] = st[st[v][j - 1 ]][j - 1 ]; dfs1 (v, u); } } int lca (int u, int v) if (dep[u] < dep[v]) swap (u, v); for (int i = 23 ; i >= 0 ; i--) if (dep[st[u][i]] >= dep[v]) u = st[u][i]; if (u == v) return u; for (int i = 23 ; i >= 0 ; i--) if (st[u][i] != st[v][i]) u = st[u][i], v = st[v][i]; return st[u][0 ]; } int dfs2 (int u) int sum = cf[u]; for (int i = fir[u]; i; i = e[i].nxt) { int v = e[i].to; if (v == st[u][0 ]) continue ; sum += dfs2 (v); ans = max (ans, sum); } return sum; } void update (int x, int y) cf[x]++; cf[y]++; int l = lca (x, y); cf[l]--; cf[st[l][0 ]]--; } int main () scanf ("%d%d" , &n, &k); for (int i = 1 ; i < n; i++) { int u, v; scanf ("%d%d" , &u, &v); add (u, v); add (v, u); } dep[1 ] = 1 ; dfs1 (1 , -1 ); for (int i = 1 ; i <= k; i++) { int x, y; scanf ("%d%d" , &x, &y); update (x, y); } dfs2 (1 ); printf ("%d\n" , ans); return 0 ; }
树的存储方式: 当作无向图
概念略
自己也是自己的祖先
公共祖先:两个点祖先的交集
最近:最靠下的公共祖先
最近公共祖先有什么用呢?
判断两个点怎么走
那么怎么求呢?
暴力?
若假定 p 1 p 2 p1 p2 p 1 p 2
可以让左右两点同时向上跳
某时刻两点重合
意味着遇到了公共祖先
调整深度 一起跳 优化:
慢是因为一步一步跳的
所以我们可以考虑每次可以每次多跳几步
f [ i ] [ j ] f [i] [j] f [ i ] [ j ] i i i 2 j 2^j 2 j
需要预处理
f [ i ] [ 0 ] = f a [ i ] f[i] [0]=fa[i] f [ i ] [ 0 ] = f a [ i ]
2 j 2^j 2 j 2 j − 1 2^{j-1} 2 j − 1 2 j − 1 2^{j-1} 2 j − 1
f [ i ] [ j ] = f [ [ i ] [ j − 1 ] ] [ j − 1 ] f[i] [j]=f[ [i] [j-1] ] [j-1] f [ i ] [ j ] = f [ [ i ] [ j − 1 ] ] [ j − 1 ]
向上跳 2 j − 1 2^{j-1} 2 j − 1
那么求出来可以有什么用呢?
求 p 1 p1 p 1 p 2 p2 p 2
最小值?
不支持修改操作。
对于 u u u v v v l c a lca l c a l c a lca l c a u u u v v v l c a lca l c a
注意区间长度本来为 d f s n y − d f s n x + 1 dfsn_{y}-dfsn_x+1 d f s n y − d f s n x + 1 [ d f s n x + 1 , d f s n y ] [dfsn_x+1,dfsn_y] [ d f s n x + 1 , d f s n y ] d f s n y − d f s n x dfsn_y-dfsn_x d f s n y − d f s n x
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 #include <iostream> #include <vector> using namespace std;const int N = 5e5 + 8 ;int idx, n, m, root, cnt;int dfsn[N], st[25 ][N], fir[N];int Log2[N];struct Edge { int to, nxt; }e[N << 1 ]; void init () Log2[0 ] = -1 ; for (int i = 1 ; i <= n; i++) Log2[i] = Log2[i / 2 ] + 1 ; } int get (int x, int y) return dfsn[x] < dfsn[y] ? x : y; } void add (int u, int v) e[++cnt].to = v; e[cnt].nxt = fir[u]; fir[u] = cnt; } void dfs (int u, int fa) dfsn[u] = ++idx; st[0 ][idx] = fa; for (int i = fir[u]; i; i = e[i].nxt) { int v = e[i].to; if (v == fa) continue ; dfs (v, u); } } int lca (int x, int y) if (x == y) return x; if (dfsn[x] > dfsn[y]) swap (x, y); int d = Log2[dfsn[y] - dfsn[x]]; return get (st[d][dfsn[x] + 1 ], st[d][dfsn[y] - (1 << d) + 1 ]); } int main () scanf ("%d%d%d" , &n, &m, &root); for (int i = 2 , u, v; i <= n; i++) { scanf ("%d%d" , &u, &v); add (u, v); add (v, u); } init (); dfs (root, 0 ); for (int i = 1 ; i <= Log2[n]; i++) for (int j = 1 ; j + (1 << i) - 1 <= n; j++) st[i][j] = get (st[i - 1 ][j], st[i - 1 ][j + (1 << (i - 1 ))]); for (int i = 1 , u, v; i <= m; i++) { scanf ("%d%d" , &u, &v); printf ("%d\n" , lca (u, v)); } return 0 ; }
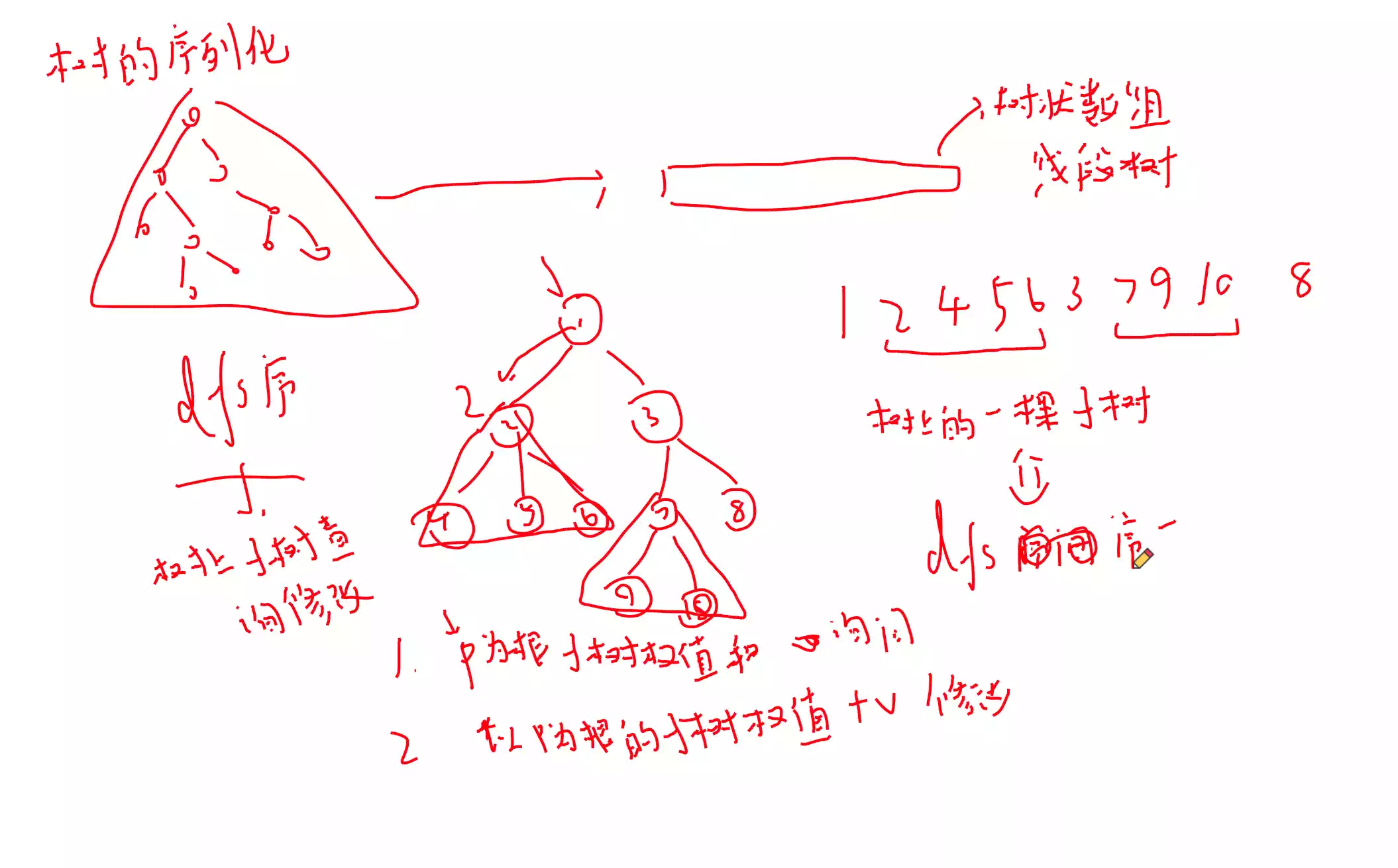
作用:树上子树查询修改以P P P 把以P P P 把根换成P P P
任何一段子树都对应一段序列上的区间
递归求出 BFS 求出 代码见 V S c o d e VScode V S c o d e
序列是写好了,那么怎样实现它的作用呢?
1. 1. 1 . 2. 2. 2 .
但是3.怎么实现呢
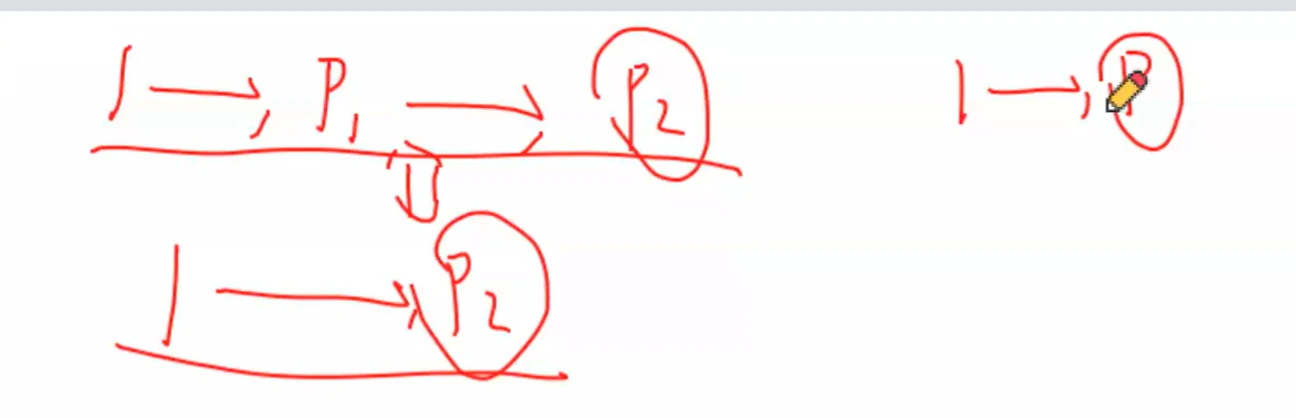
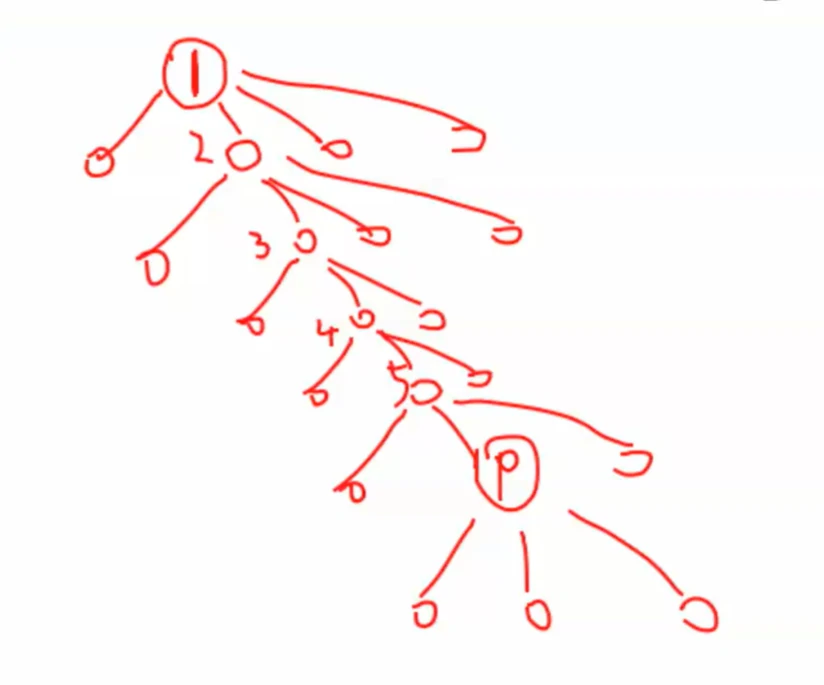
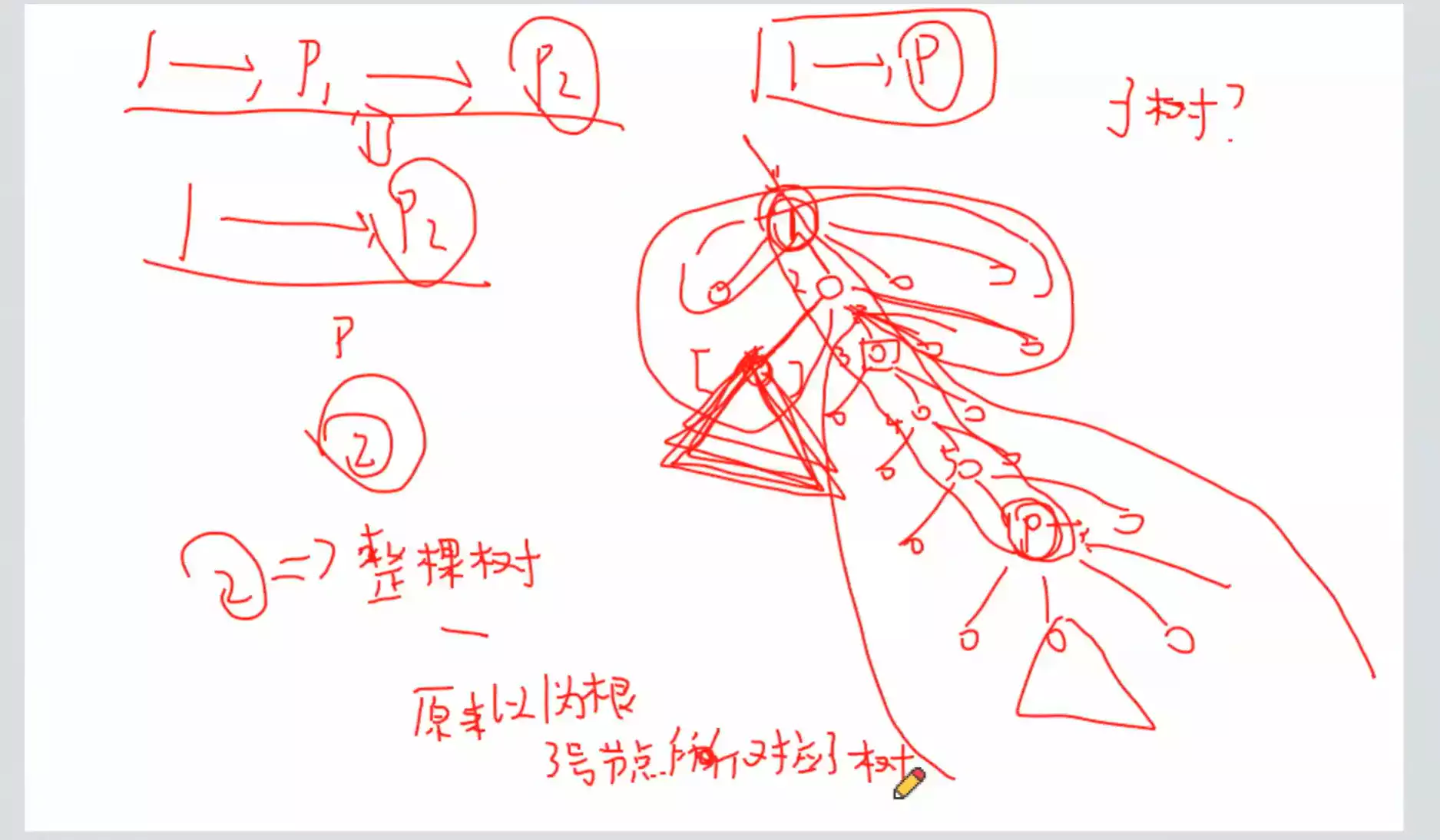
会改变 dfs 序
解决方法:
只换一次
哪些点的子树会发生变化?
只有1 1 1 p p p
不会影响其它点
把一段区间的询问改成两段区间的询问就可以了
它能解决什么样的问题呢?
链上操作
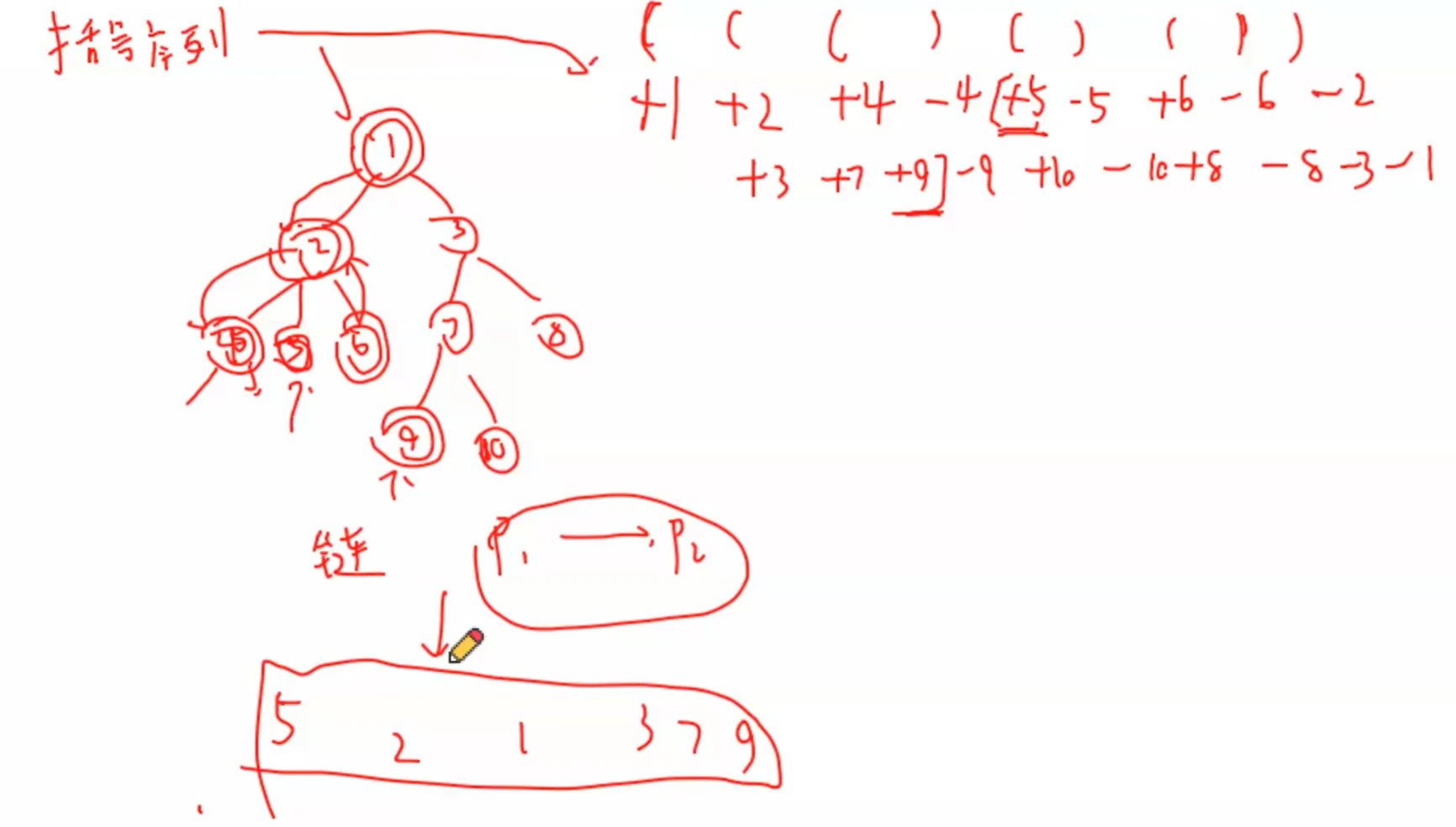
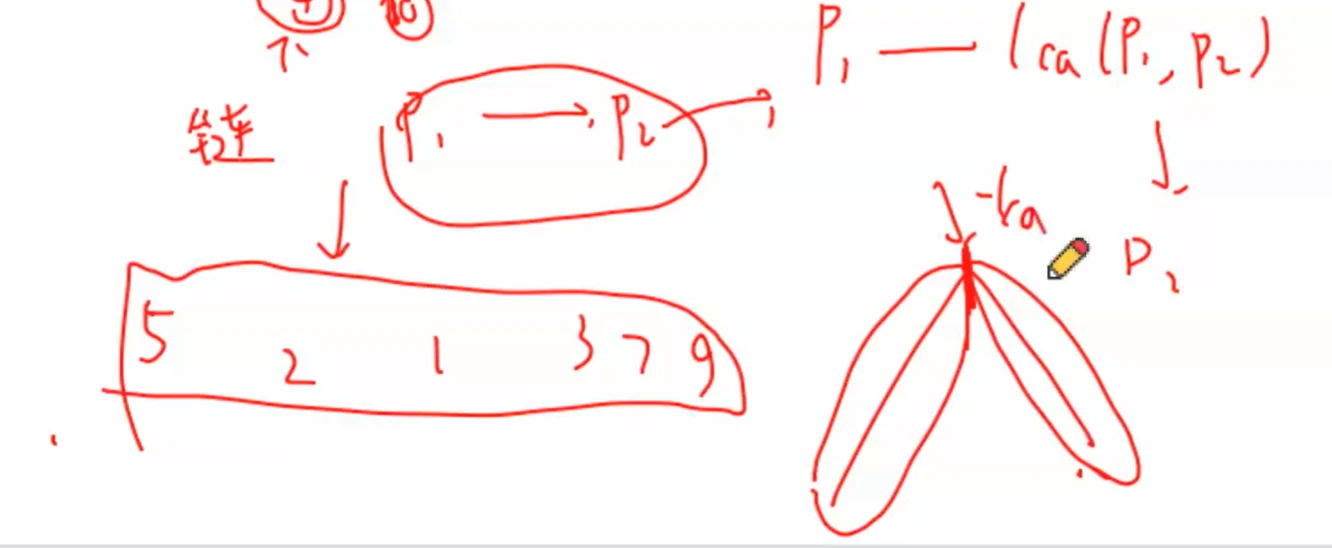
用 LCA 把这段链分成两部分
这样就可以分别进行求解( 可能LCA被算了两次,减去一个就可以了 )
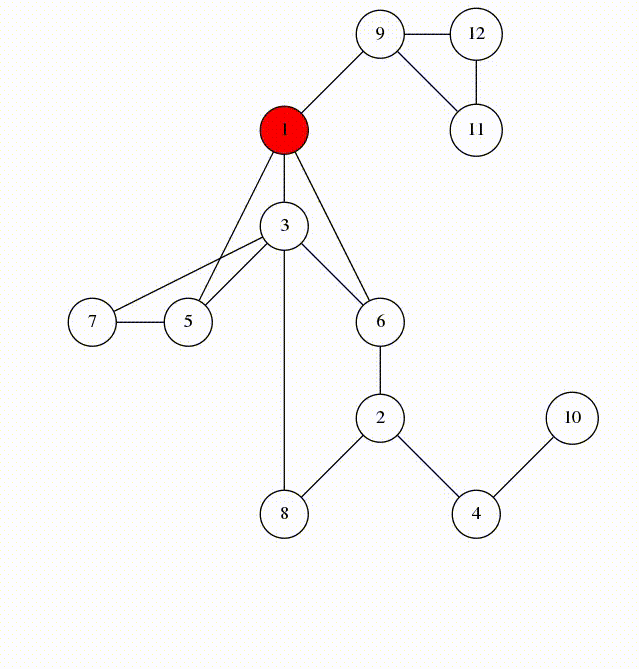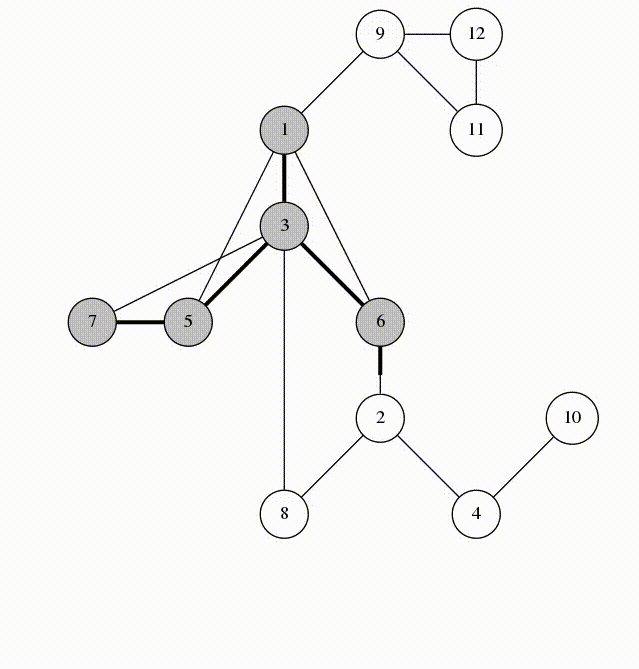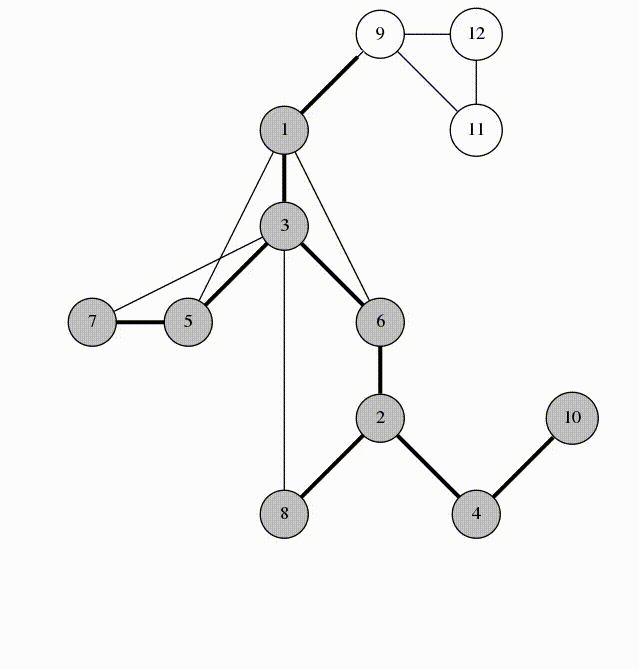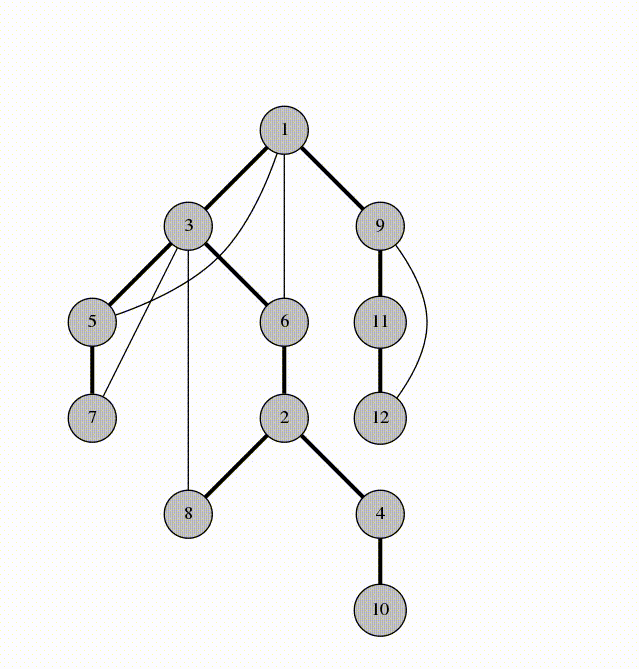
5 → 1 5 \to 1 5 → 1
1 → 9 1 \to 9 1 → 9
链求和转换为两端区间求和
只能用来求链的和
不能求最大值最小值
可以用倍增来做
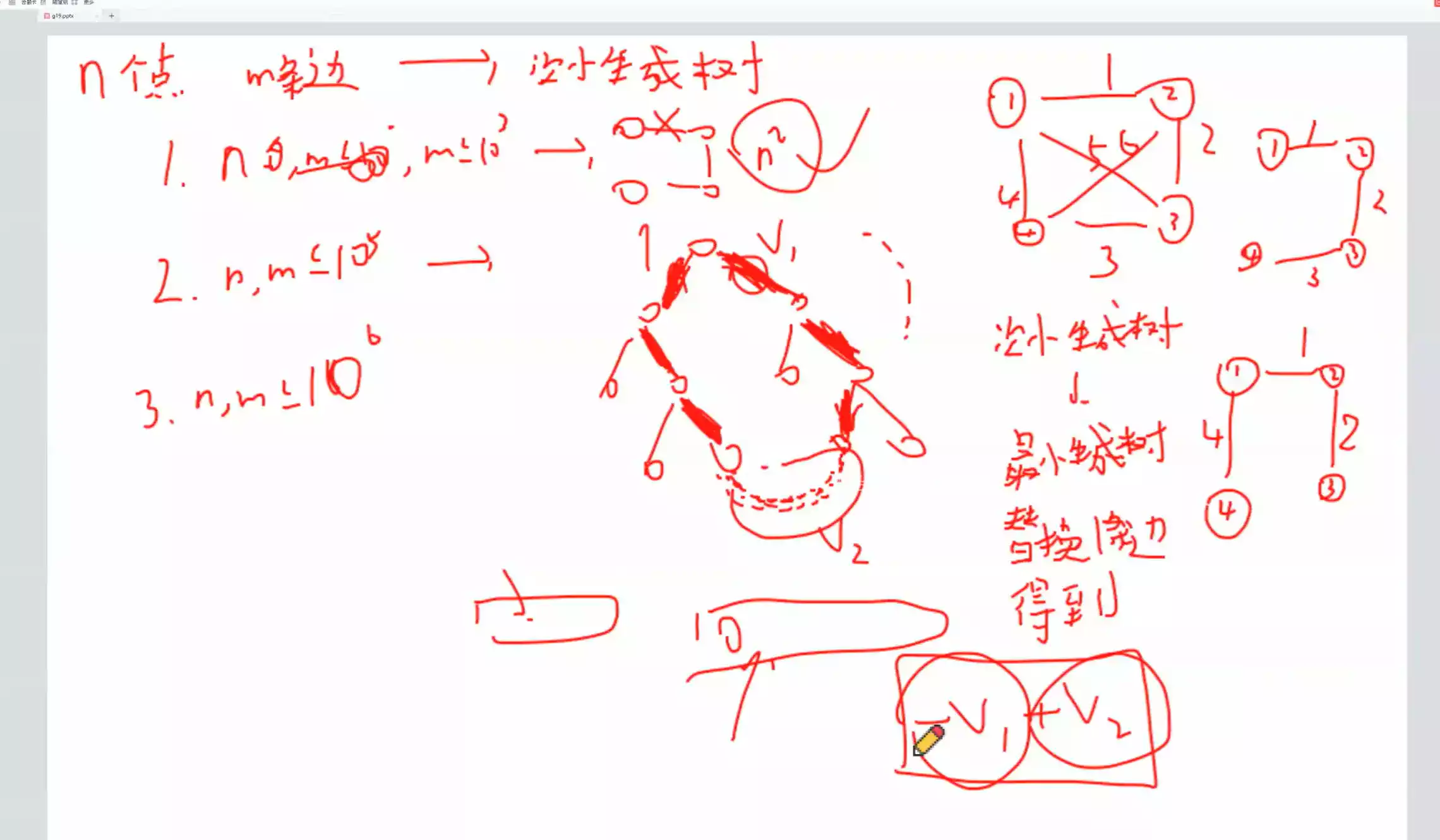
概念:n n n n − 1 n-1 n − 1 每次选择与生成树这个连通块的最小的一条连接的边,加到这个连通块内。
维护两个集合:
左边的集合:还没有加到生成树中的点
右边的集合:加到生成树的点
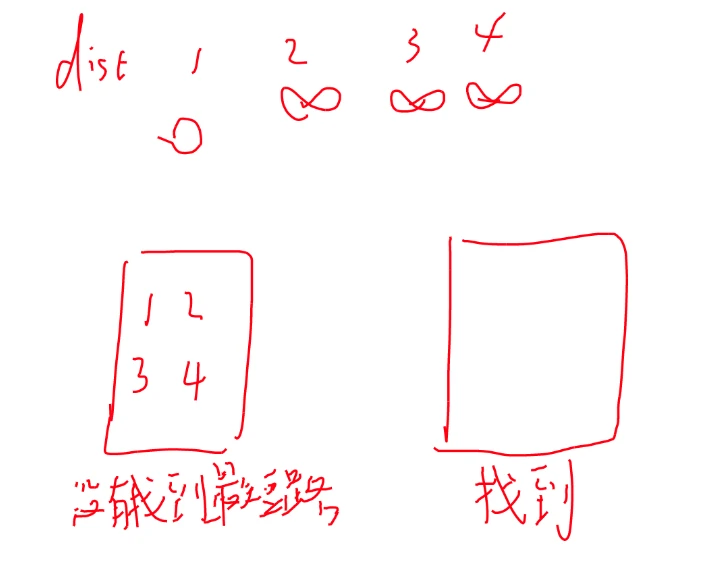
d i s t dist d i s t 生成树 上的最短距离
走不到就是无穷大(初始化)
一开始生成树上是没有点的
所以点 1 1 1 d i s t dist d i s t 0 0 0
然后用一号点更新其他点
每轮选左边 d i s t dist d i s t
把所有点都放到右边以后就做完了
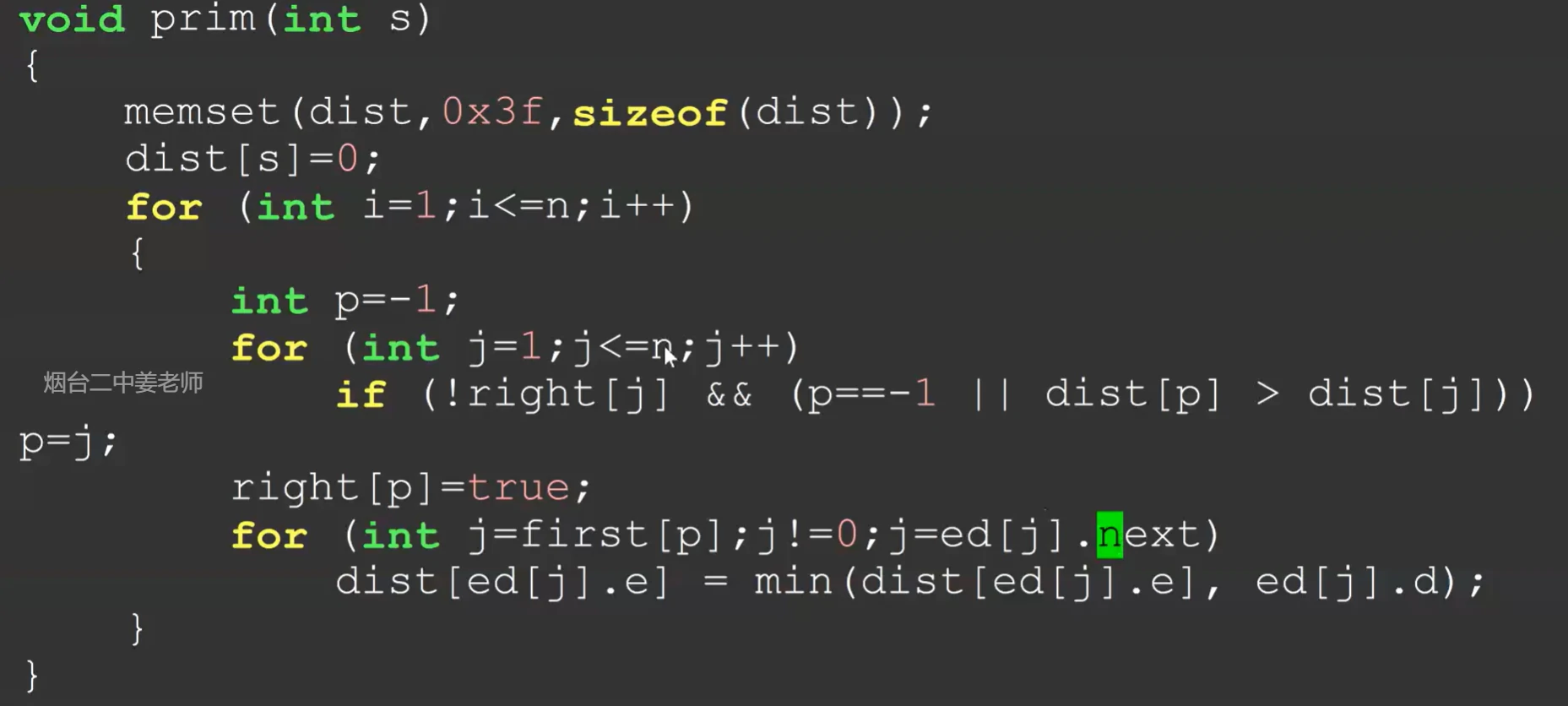
这就是PRIM 算法(Djkstra的孪生兄弟 )
它与 Dijkstra 最大的不同就是 Dijkstra 维护的是到起点的距离,而 Prim 维护的是到已经生成的最小生成树的连通块的距离。
堆优化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 void prim (int s) memset (dist, 0x3f , sizeof (dist)); dist[s] = 0 ; heap.push (point (s, dist[s])); while (heap.size ()) { auto t = heap.top (); heap.pop (); if (vis[t.p]) continue ; vis[t.p] = true ; for (int i = fir[t.p]; i; i = ed[i].next) { int v = ed[i].e; if (ed[i].d < dist[v]) { dist[v] = ed[i].d; heap.push (point (v, dist[v])); } } } }
n 2 n^2 n 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 int prim () vis[1 ] = 1 ; int res = 0 ; for (int i = 1 ; i <= n; i ++) dist[i] = graph[1 ][i]; for (int j = 1 ; j <= n; j ++) { int minc = INF, p; for (int i = 1 ; i <= n; i++){ if (vis[i] == 0 && dist[i] < minc) { minc = dist[i]; p = i; } } if (minc == INF) return -1 ; vis[p] = 1 ; res += dist[p]; for (int i = 1 ; i <= n; i ++) { if (vis[i] == 0 && dist[i] > graph[p][i]) dist[i] = graph[p][i]; } } return res; }
复杂度:O ( ( N + M ) l o g N ) O((N+M)logN) O ( ( N + M ) l o g N )
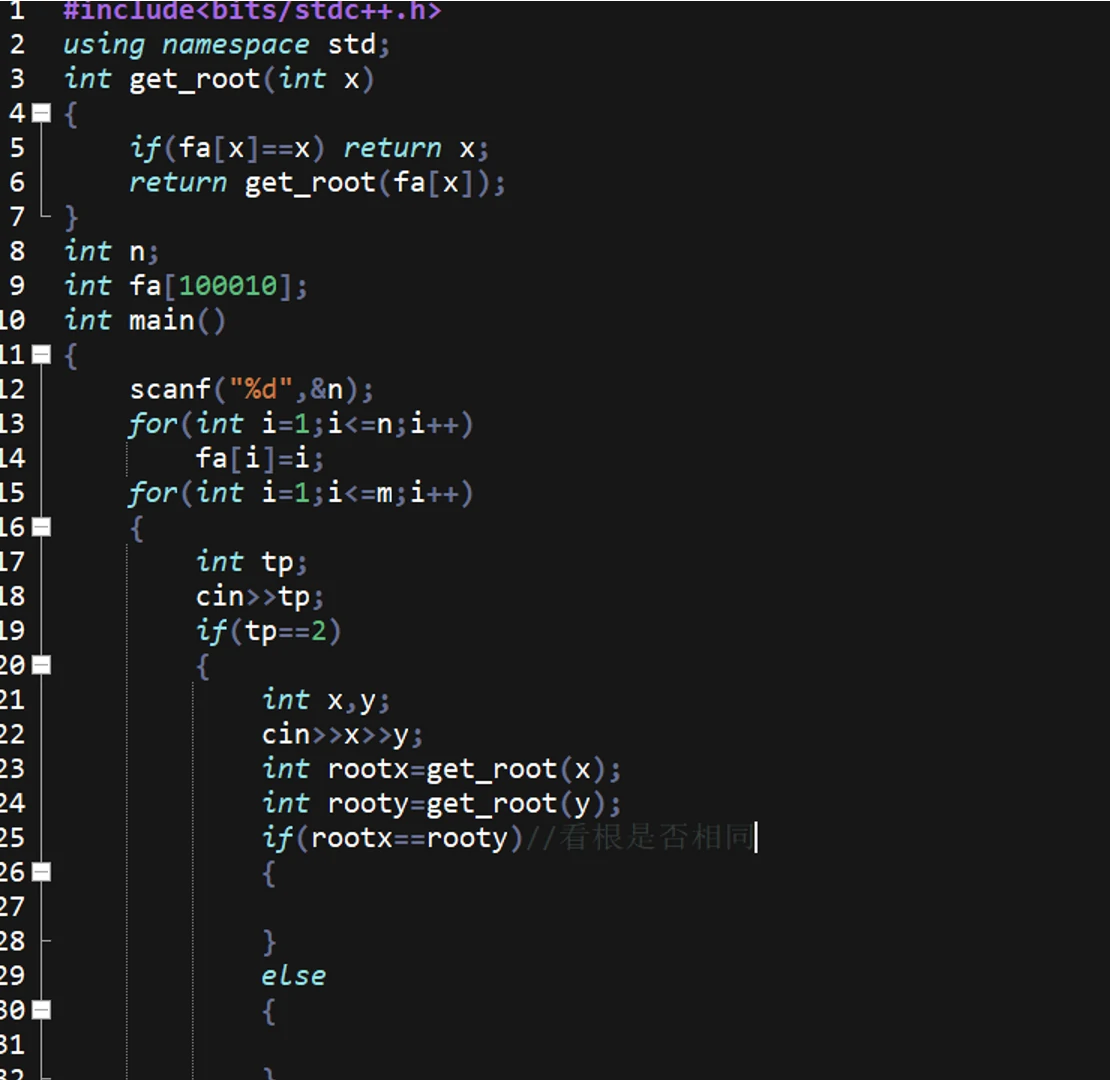
支持两种操作:
代码也是十分的好写啊
假如是条链呢?
那这样就太慢了
我们可以进行一些优化
之前不是谁都可以做父亲吗
现在谁的子树大,谁就是父亲
谁的深度大,谁就是父亲
不改变合并过程
但在get_root找根的时候
把所有点的父亲都变成根
因为我们不关心树上的父子关系,我们只关心根是谁
贪心+并查集
将边从小到大排序,从小到大每次挑一个加入到最小生成树中,若形成环则跳过,判断环可以用并查集实现。
当在边数远大于点数的稠密图中,Kruskal 会重复判断一些边导致超时,这时 Prim 更优。
所以 Kruskal 适合边数较少的稀疏图。
AcWing1140
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <bits/stdc++.h> using namespace std;const int N = 110 ;int n;int w[N][N];int dist[N];bool st[N];int prim () int res = 0 ; memset (dist, 0x3f , sizeof (dist)); dist[1 ] = 0 ; for (int i = 1 ; i <= n; i++) { int t = -1 ; for (int j = 1 ; j <= n; j++) if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j; res += dist[t]; st[t] = true ; for (int j = 1 ; j <= n; j++) dist[j] = min (dist[j], w[t][j]); } return res; } int main () cin >> n; for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= n; j++) cin >> w[i][j]; cout << prim () << endl; return 0 ; }
AcWing1141
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 #include <bits/stdc++.h> using namespace std;const int N = 110 , M = 210 ;int n, m;int p[N];struct edge { int a, b, w; bool operator < (const edge &t) const { return w < t.w; } }e[M]; int find (int x) if (p[x] != x) p[x] = find (p[x]); return p[x]; } int main () cin >> n >> m; for (int i = 1 ; i <= n; i++) p[i] = i; for (int i = 1 ; i <= m; i++) { int a, b, c; cin >> a >> b >> c; e[i] = {a, b, c}; } sort (e + 1 , e + 1 + m); int res = 0 ; for (int i = 1 ; i <= m; i++) { int a = find (e[i].a), b = find (e[i].b), w = e[i].w; if (a != b) p[a] = b; else res += w; } cout << res << endl; return 0 ; }
AcWing1142
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <bits/stdc++.h> using namespace std;const int N = 310 , M = 11111 ;int n, m;int p[N];struct edge { int a, b, w; bool operator < (const edge &t) const { return w < t.w; } }e[M]; int find (int x) if (p[x] != x) p[x] = find (p[x]); return p[x]; } int main () cin >> n >> m; for (int i = 1 ; i <= n; i++) p[i] = i; for (int i = 0 ; i < m; i++) cin >> e[i].a >> e[i].b >> e[i].w; sort (e, e + m); int res = 0 ; for (int i = 0 ; i < m; i++) { int a = find (e[i].a), b = find (e[i].b); int w = e[i].w; if (a != b) { p[a] = b; res = w; } } cout << n - 1 << ' ' << res << endl; return 0 ; }
AcWing1143
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <bits/stdc++.h> using namespace std;const int N = 2200 , M = 10010 ;int p[N];int n, m;struct edge { int a, b, w; bool operator < (const edge &t) const { return w < t.w; } }e[M]; int find (int x) if (x != p[x]) p[x] = find (p[x]); return p[x]; } int main () cin >> n >> m; int cnt = 0 ; int res = 0 ; for (int i = 1 ; i <= n; i++) p[i] = i; for (int i = 0 ; i < m; i++) { int g, u, v, w; cin >> g >> u >> v >> w; if (g == 1 ) { int a = find (u), b = find (v); p[a] = b; res += w; } else e[++cnt] = {u, v, w}; } sort (e + 1 , e + 1 + cnt); for (int i = 1 ; i <= cnt; i++) { int a = find (e[i].a), b = find (e[i].b); if (a != b) { p[a] = b; res += e[i].w; } } cout << res << endl; return 0 ; }
AcWing1144
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 #include <bits/stdc++.h> using namespace std;const int N = 1010 , M = 2e6 + 7 ; int n, m;int ids[N][N];int p[N * N];int cnt;struct edge { int a, b, w; }e[M]; int find (int x) if (x != p[x]) p[x] = find (p[x]); return p[x]; } void get_edges () int dx[] = {1 , 0 , -1 , 0 }; int dy[] = {0 , 1 , 0 , -1 }; int dw[] = {1 , 2 , 1 , 2 }; for (int z = 0 ; z < 2 ; z++) for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= m; j++) for (int u = 0 ; u < 4 ; u++) if ((u & 1 ) == z) { int x = i + dx[u], y = j + dy[u]; int w = dw[u]; if (x < 0 || x > n || y < 0 || y > m) continue ; int a = ids[i][j], b = ids[x][y]; if (a < b) e[++cnt] = {a, b, w}; } } int main () cin >> n >> m; int res = 0 ; int x1, y1, x2, y2; for (int i = 1 , t = 1 ; i <= n; i++) for (int j = 1 ; j <= m; j++, t++) ids[i][j] = t; for (int i = 1 ; i <= n * m; i++) p[i] = i; while (cin >> x1 >> y1 >> x2 >> y2) { int a = ids[x1][y1], b = ids[x2][y2]; p[find (a)] = find (b); } get_edges (); for (int i = 1 ; i <= cnt; i++) { int a = find (e[i].a), b = find (e[i].b), w = e[i].w; if (a != b) { p[a] = b; res += w; } } cout << res << endl; return 0 ; }
任意一颗最小生成树一定可以包含无向图中最小的边。 给定一张无向图,若从中选出小于 n − 1 n - 1 n − 1 m − k m - k m − k m − k m - k m − k AcWing1146
虚拟源点的思想。
让这 n + 1 n + 1 n + 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;const int N = 310 ;int n;int w[N][N];int dist[N];bool st[N];int prim () memset (dist, 0x3f , sizeof (dist)); dist[0 ] = 0 ; int res = 0 ; for (int i = 0 ; i <= n; i++) { int t = -1 ; for (int j = 0 ; j <= n + 1 ; j ++) if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j; st[t] = true ; res += dist[t]; for (int j = 0 ; j <= n; j++) dist[j] = min (dist[j], w[t][j]); } return res; } int main () scanf ("%d" , &n); for (int i = 1 ; i <= n; i++) { scanf ("%d" , &w[0 ][i]); w[i][0 ] = w[0 ][i]; } for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= n; j++) scanf ("%d" , &w[i][j]); printf ("%d\n" , prim ()); return 0 ; }
AcWing1145
可以先二分后遍历。
也可以用并查集维护连通块的数量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 #include <bits/stdc++.h> using namespace std;const int N = 510 , M = N * N / 2 ;typedef pair<int , int > PII;#define x first #define y second int n, k, m;PII q[M]; int p[N];struct edge { int a, b; double w; bool operator < (const edge &t) const { return w < t.w; } }e[M]; double dist (int a, int b) int dx = q[a].x - q[b].x; int dy = q[a].y - q[b].y; return sqrt (dx * dx + dy * dy); } int find (int x) if (x != p[x]) p[x] = find (p[x]); return p[x]; } int main () cin >> n >> k; for (int i = 1 ; i <= n; i++) cin >> q[i].x >> q[i].y; for (int i = 1 ; i <= n; i++) for (int j = 1 ; j < i; j++) e[++m] = {i, j, dist (i, j)}; sort (e + 1 , e + m + 1 ); for (int i = 1 ; i <= n; i++) p[i] = i; int cnt = n; double res = 0 ; for (int i = 1 ; i <= m; i++) { if (cnt == k) break ; int a = find (e[i].a), b = find (e[i].b); double w = e[i].w; if (a != b) { p[a] = b; cnt--; res = w; } } printf ("%.2lf\n" , res); return 0 ; }
AcWing346
每次合并连通块的时候,要把这两个连通块变成一张完全图,这样合并到最后得到的也是完全图。
加边,最小只能加原来的边权加一,因为要保证最小生成树不变且唯一。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <bits/stdc++.h> using namespace std;const int N = 6010 ;const int M = (N * N) >> 1 ;int n;int p[N], siz[N];struct edge { int a, b, w; bool operator < (const edge &t) const { return w < t.w; } }e[M]; int find (int x) if (x != p[x]) p[x] = find (p[x]); return p[x]; } int main () int t; cin >> t; while (t--) { cin >> n; for (int i = 1 ; i < n; i++) scanf ("%d%d%d" , &e[i].a, &e[i].b, &e[i].w); sort (e + 1 , e + n); for (int i = 1 ; i <= n; i++) p[i] = i, siz[i] = 1 ; int res = 0 ; for (int i = 1 ; i < n; i++) { int a = find (e[i].a), b = find (e[i].b); int w = e[i].w; if (a != b) { res += (siz[a] * siz[b] - 1 ) * (w + 1 ); siz[b] += siz[a]; p[a] = b; } } cout << res << endl; } return 0 ; }
AcWing1148
严格次小生成树。
先求最小生成树,然后依次枚举删去最小生成树中的边再跑最小生成树。 这样做是 O ( m l o g m + n m ) O(mlogm + nm) O ( m l o g m + n m )
这样做得到的只是次小生成树,不保证严格次小。
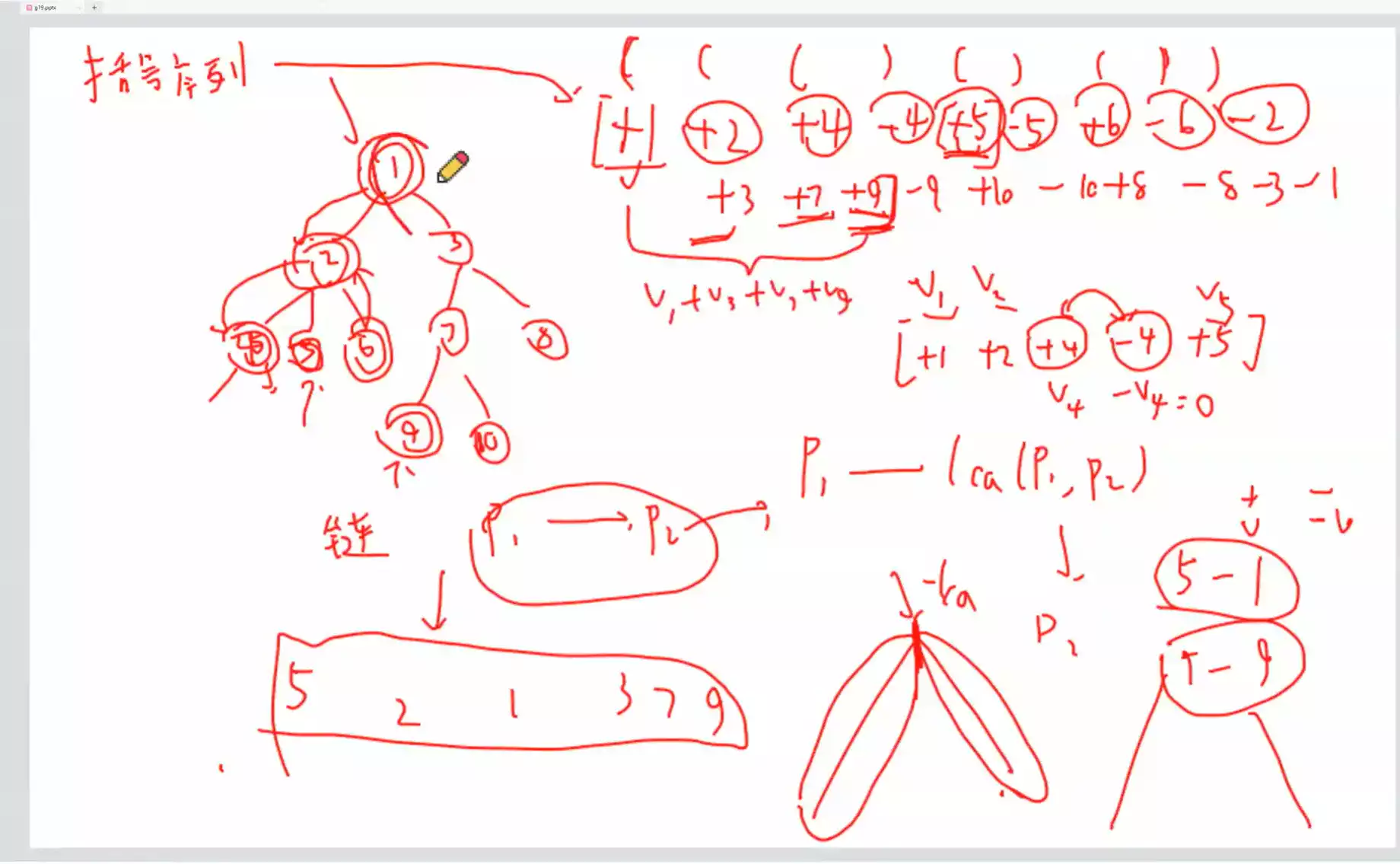
先求最小生成树,然后依次枚举非树边,然后将该边加入树中,同时从树中这个环上任意去掉一条边,使得最终的图是一颗树,那么一定能求出次小生成树。 要保证求得是仅次于最小的最小,所以删去的边要尽可能大,其实就是求树上任意两点间的一个极值,这个可以用倍增来做,也可以暴力预处理。
复杂度: n 2 + m n^{2}+m n 2 + m
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 #include <bits/stdc++.h> using namespace std;const int N = 510 , M = 10010 ;typedef long long ll;int n, m, cnt;int p[N];int dist[N][N];int dist2[N][N];struct edge { int a, b, w; bool f = false ; bool operator < (const edge &t) const { return w < t.w; } }ed[M]; struct Edge { int nxt, to, val; }e[N << 1 ]; int fir[N];void add (int u, int v, int w) e[++cnt].to = v; e[cnt].nxt = fir[u]; e[cnt].val = w; fir[u] = cnt; } int find (int x) if (x != p[x]) p[x] = find (p[x]); return p[x]; } void dfs (int u, int fa, int maxd, int maxd2, int d[], int d2[]) d[u] = maxd, d2[u] = maxd2; for (int i = fir[u]; i; i = e[i].nxt) { int v = e[i].to; if (v == fa) continue ; int td1 = maxd, td2 = maxd2; if (e[i].val > td1) { td2 = td1; td1 = e[i].val; } else if (e[i].val < maxd && e[i].val > maxd2) td2 = e[i].val; dfs (v, u, td1, td2, d, d2); } } int main () scanf ("%d%d" , &n, &m); for (int i = 1 ; i <= m; i++) { int a, b, w; scanf ("%d%d%d" , &a, &b, &w); ed[i] = {a, b, w}; } sort (ed + 1 , ed + m + 1 ); for (int i = 1 ; i <= n; i++) p[i] = i; ll sum = 0 ; for (int i = 1 ; i <= m; i++) { int a = ed[i].a, b = ed[i].b; int pa = find (a), pb = find (b), w = ed[i].w; if (pa != pb) { p[pa] = pb; sum += w; add (a, b, w); add (b, a, w); ed[i].f = true ; } } ll res = 1e18 ; for (int i = 1 ; i <= n; i++) dfs (i, -1 , -1e9 , -1e9 , dist[i], dist2[i]); for (int i = 1 ; i <= m; i++) if (!ed[i].f) { int a = ed[i].a, b = ed[i].b, w = ed[i].w; if (w > dist[a][b]) res = min (res, sum + w - dist[a][b]); else if (w > dist2[a][b]) res = min (res, sum + w - dist2[a][b]); } printf ("%lld\n" , res); return 0 ; }
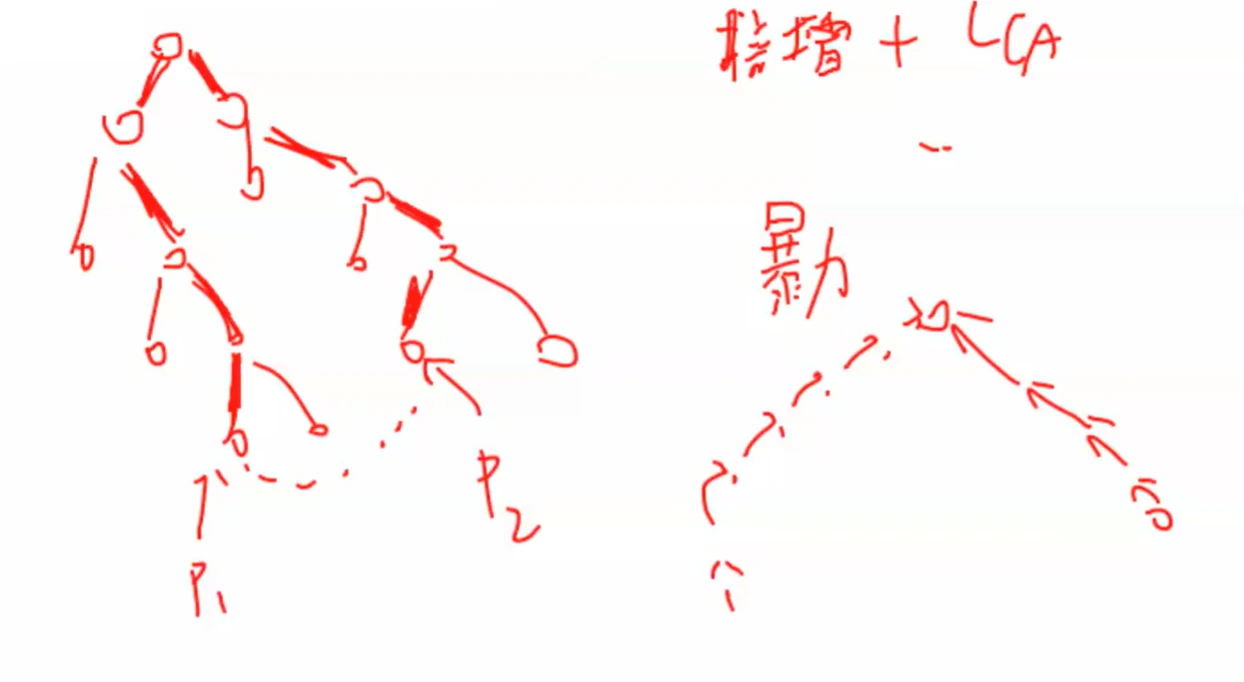
我们发现次小生成树肯定是通过最小生成树来求的(替换一条边)
路径上找到最大的 V1 进行替换
换为V 2 V_2 V 2
怎么找最大的边呢?
进行一个倍增 LCA
在 LCA 的过程中找到最大值
1.先求最小生成树
2.用非树上的边替换树上链的最大值
3.求最大值可以用 LCA 来做
我不倍增求了
我暴力!
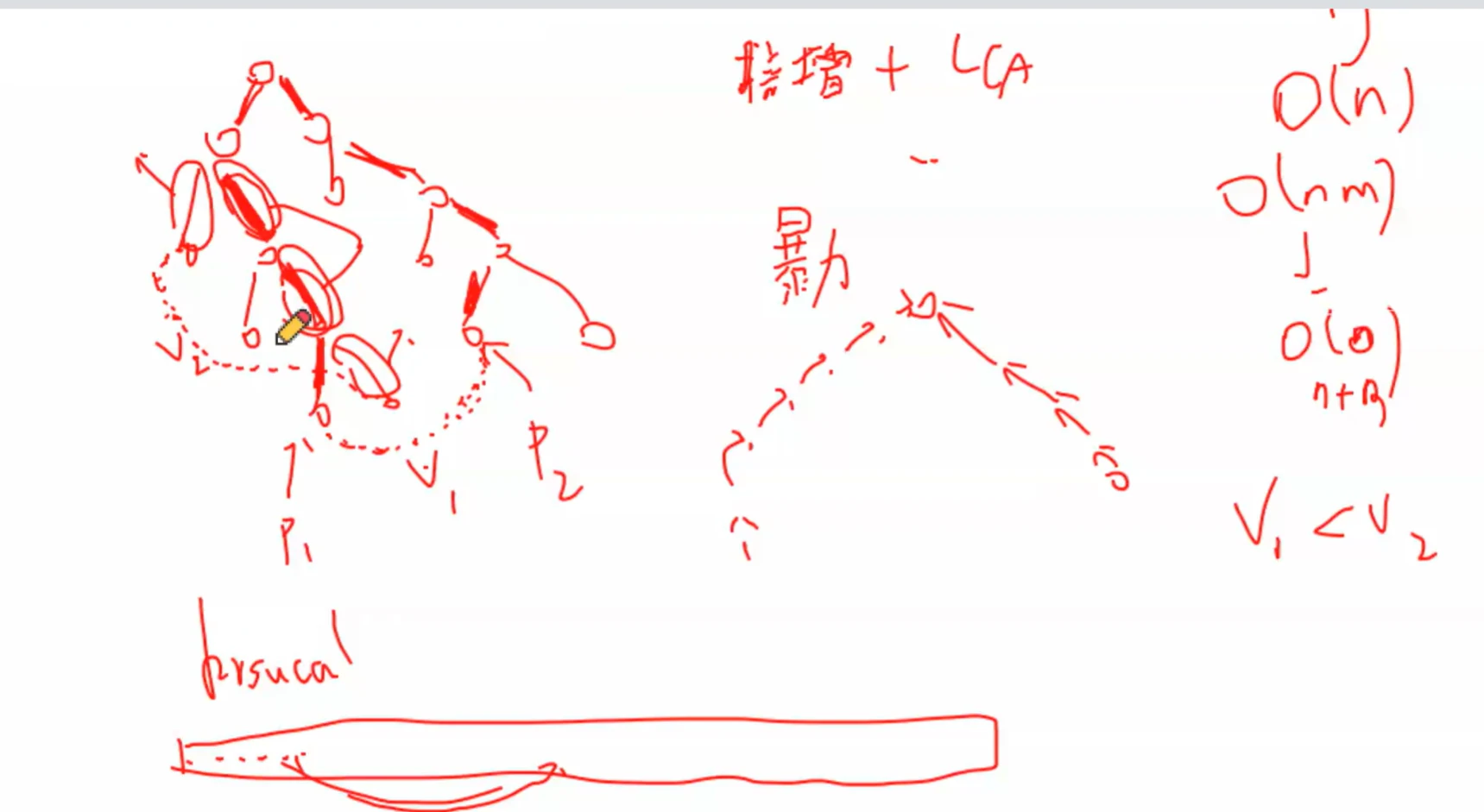
O ( n m ) O(nm) O ( n m )
因为 Kruscal 求的时候对每条边排了个序
所以可以用排的序对非树边从小到大去枚举
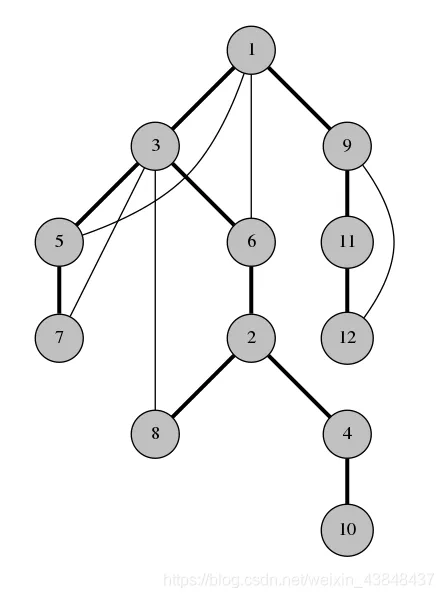
以这张图为例
先一点点求一个V 1 V_1 V 1
然后V 2 V_2 V 2 V 1 V_1 V 1
我们发现在V 2 V_2 V 2 V 1 V_1 V 1
假如用V 2 V_2 V 2
设加粗边中的一条长度为a a a
那么分别替换后树的变化
很明显,在V 1 V_1 V 1 a a a V 2 V_2 V 2 a a a
而在V 1 V_1 V 1 a a a
所以V 2 V_2 V 2 a a a
因为拿V 1 V_1 V 1 a a a
换而言之
一条边之前已经被更小的边判断过了
拿更大的边去判断已经判断过的边是没有意义的
也就是把非树边从小到大枚举
整个树上的边最多只需要被判断一次就够了
所以复杂度就变为了O ( m + n ) O(m+n) O ( m + n )
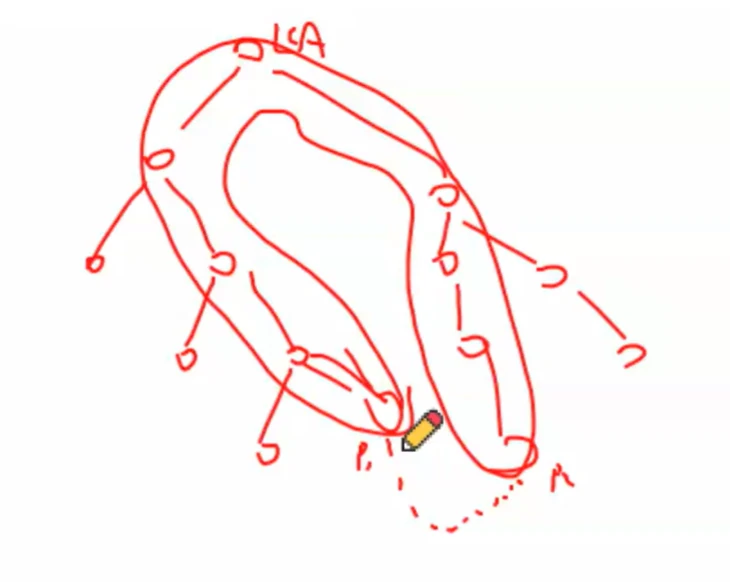
那怎么保证只判断一次呢?
遍历一次就把它删掉
当然是用并查集咯
假设这是第一次遍历
那么就把这条路径上的点并为一个集合
第二次遍历
因为右下角的那个点更深,因此向上跳
发现跳到了之前已经跳到过的点
那么就直接跳到它的祖先
也就是向上跳一步
就把它加到它父亲的并查集里
再跳到它父亲的祖先位置
换句话说
假如某条边已经被考虑过了
那么就把它连接的两个点加到同一个并查集中
这样就可以保证每个点只访问了一次
并查集O ( 1 ) O(1) O ( 1 )
一条路径经过所有的边且只经过一次。
若起点和终点相同,则称之为欧拉回路 。
无向图存在欧拉回路的条件:所有点的度数都为偶数。
无向图存在欧拉路径: 恰有两个点度数为奇数(起点和终点)。
有向图存在欧拉回路:所有点都满足 入度等于出度 。
有向图存在欧拉路径:恰有一个点入度比出度多一(终点),另一个点出度比入度多一,其余点入度和出度相同。
从起点开始 DFS ,然后枚举它的出边,继续 DFS 。
走过的边都标记(删边),遇到走过的边就continue。
回溯的时候再压入栈内,因为如果一开始就压栈,
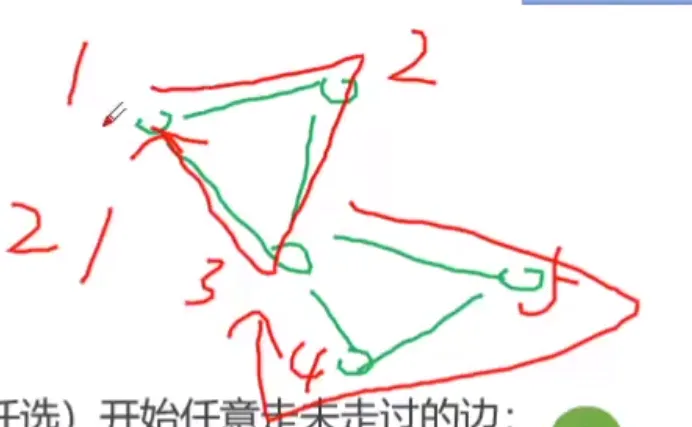
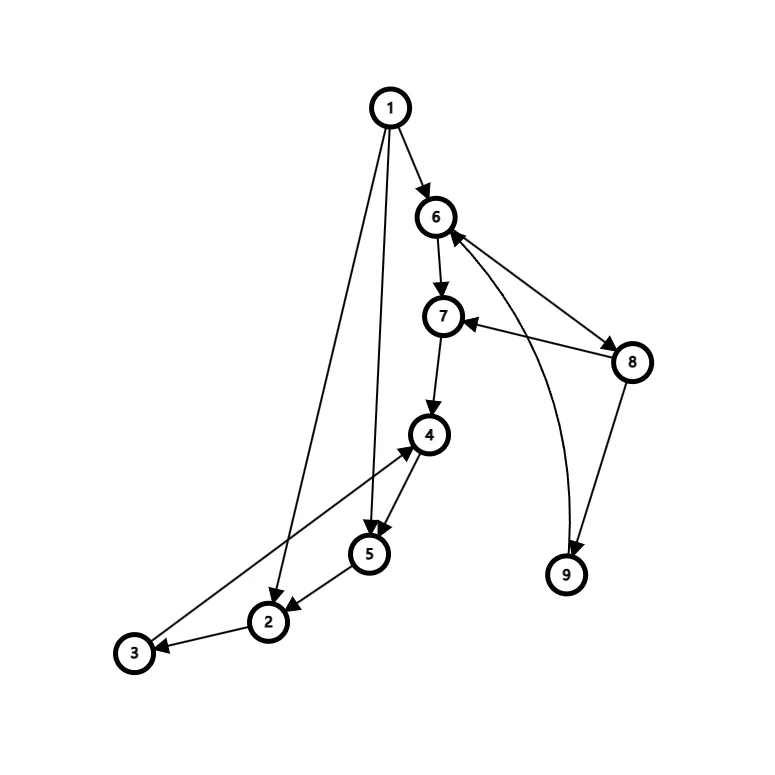
看这张图,1 → 2 → 3 1\to{2}\to{3} 1 → 2 → 3
遍历到 3 3 3 123 1 2 3 1 2 3
然后再遍历 3 3 3 3 → 1 3\to{1} 3 → 1 3 → 1 3\to{1} 3 → 1 4 4 4 5 5 5
所以我们可以回溯后再让它进栈,因为这样的话遍历到 1 1 1 1 1 1 3 3 3 1 1 1 3 → 5 → 4 → 3 3\to{5}\to{4}\to{3} 3 → 5 → 4 → 3 3 3 3 3 → 1 3\to{1} 3 → 1 3 3 3
再举个例子便于理解:
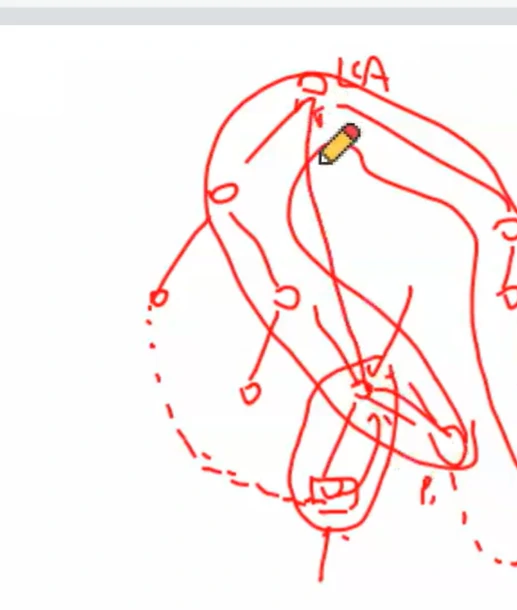
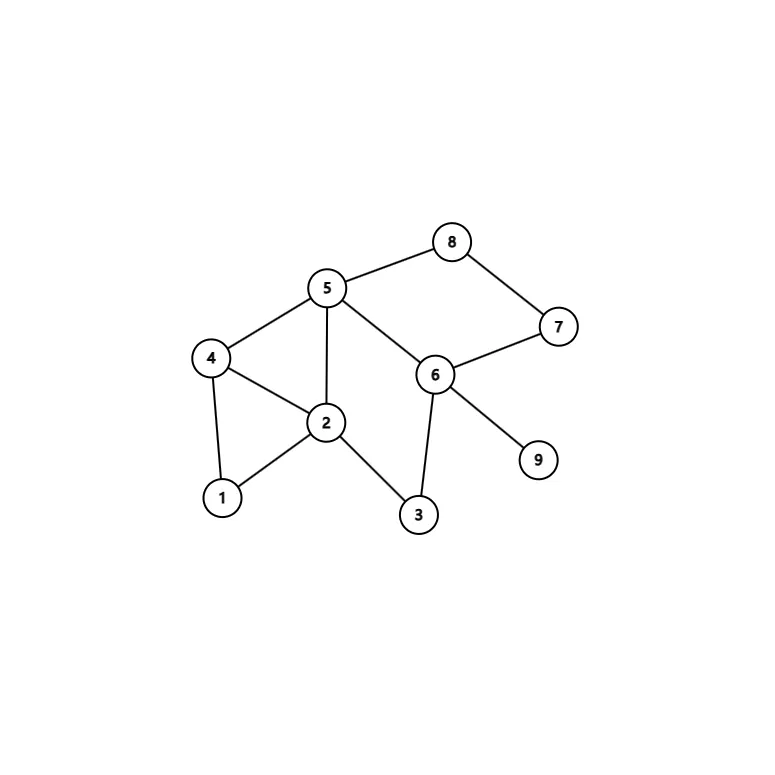
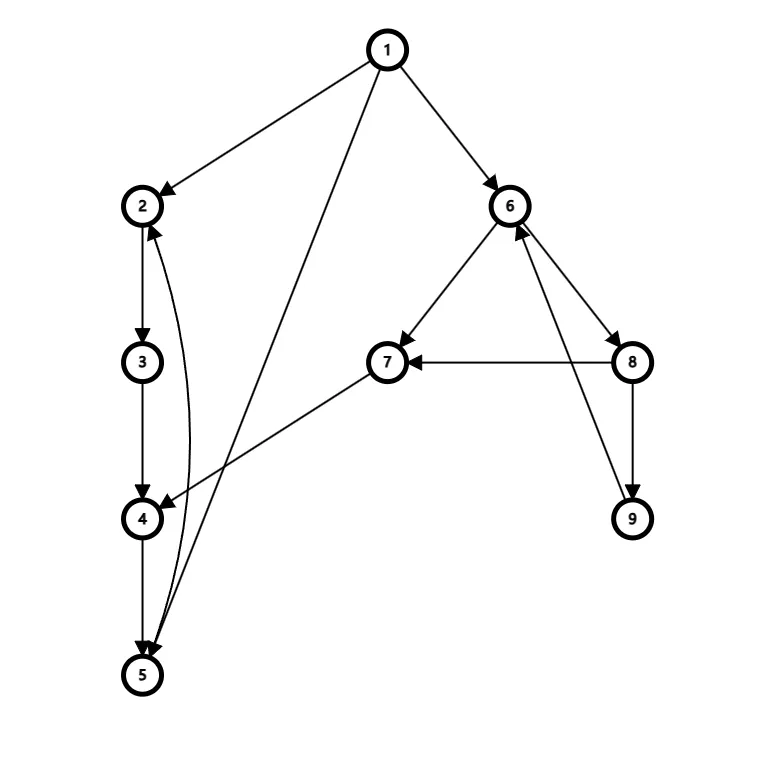
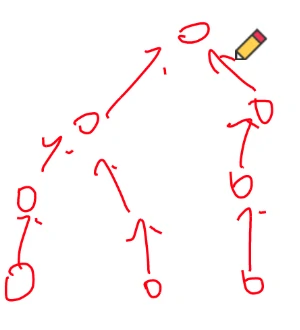
对于这样一张图,
如果先递归后压栈,那么得到的欧拉路径为:
9 → 6 → 3 → 2 → 1 → 4 → 2 → 5 → 6 → 7 → 8 → 5 → 4 {9}\to{6}\to{3}\to{2}\to{1}\to{4}\to{2}\to{5}\to{6}\to{7}\to{8}\to{5}\to{4} 9 → 6 → 3 → 2 → 1 → 4 → 2 → 5 → 6 → 7 → 8 → 5 → 4
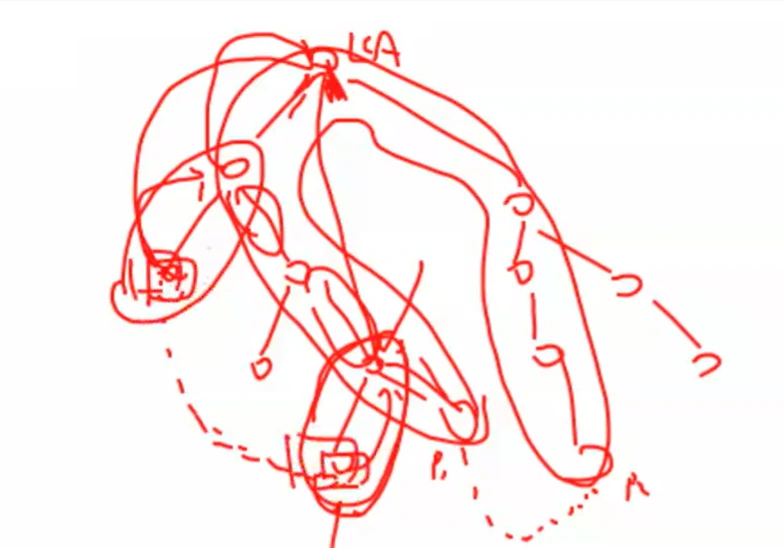
如果先压栈后递归,得到的欧拉路径为:
9 → 6 → 3 → 2 → 1 → 4 → 2 → 5 → 4 → 6 → 7 → 8 → 5 {9}\to{6}\to{3}\to{2}\to{1}\to{4}\to{2}\to{5}\to{4}\to{6}\to{7}\to{8}\to{5} 9 → 6 → 3 → 2 → 1 → 4 → 2 → 5 → 4 → 6 → 7 → 8 → 5
这里后半段应该是 5 → 6 → 7 → 8 → 5 → 4 {5}\to{6}\to{7}\to{8}\to{5}\to{4} 5 → 6 → 7 → 8 → 5 → 4 5 5 5 4 4 4 5 → 6 → 7 → 8 {5}\to{6}\to{7}\to{8} 5 → 6 → 7 → 8
对于有向图,最后压栈的是前几个被遍历的,因此答案是反的,想办法 reverse 一下就好了。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 #include <bits/stdc++.h> using namespace std;int n,m,st,cnt;int d[1000 ][1000 ],ans[1000 ],f[1000 ];stack<int > S; void dfs (int u) for (int v=1 ;v<=n;v++) { if (d[u][v]) { d[u][v]--,d[v][u]--; dfs (v); } } S.push (u); } int main () int p=0 ; scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=m;i++) { int a,b; scanf ("%d%d" ,&a,&b); d[a][b]++,d[b][a]++; f[a]++,f[b]++; } for (int i=1 ;i<=n;i++) { if (f[i]%2 ==1 ) { st=i; cnt++; } } if (cnt!=2 ) { cout<<"No" <<endl; return 0 ; } cout<<st<<endl; dfs (st); while (!S.empty ()) { ans[++p]=S.top (); S.pop (); } reverse (ans+1 ,ans+p+1 ); for (int i=1 ;i<=p;i++) printf ("%d " ,ans[i]); return 0 ; }
对于链式前向星,也可以这样写:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int edcnt = 1 ;stack<int > ans; void dfs (int x) for (int i = head[x];i;i = nex[i]) { int y = to[i]; if (vis[i]) continue ; vis[i] = 1 ; vis[i ^ 1 ] = 1 ; dfs (y); } ans.push (x); }
还可以这样写
1 2 3 4 5 6 7 8 9 10 void ola (int x) for (int i=fir[x];i;i=fir[x]) { int v=e[i].to; fir[x]=e[i].nxt; ola (v); } S.push (x); }
这样就相当于直接在原图上进行修改了。
BZOJ3724 Krolestwo:
题解
AcWing366
本题建立双向边的有向图,边数× 2 \times{2} × 2
题解
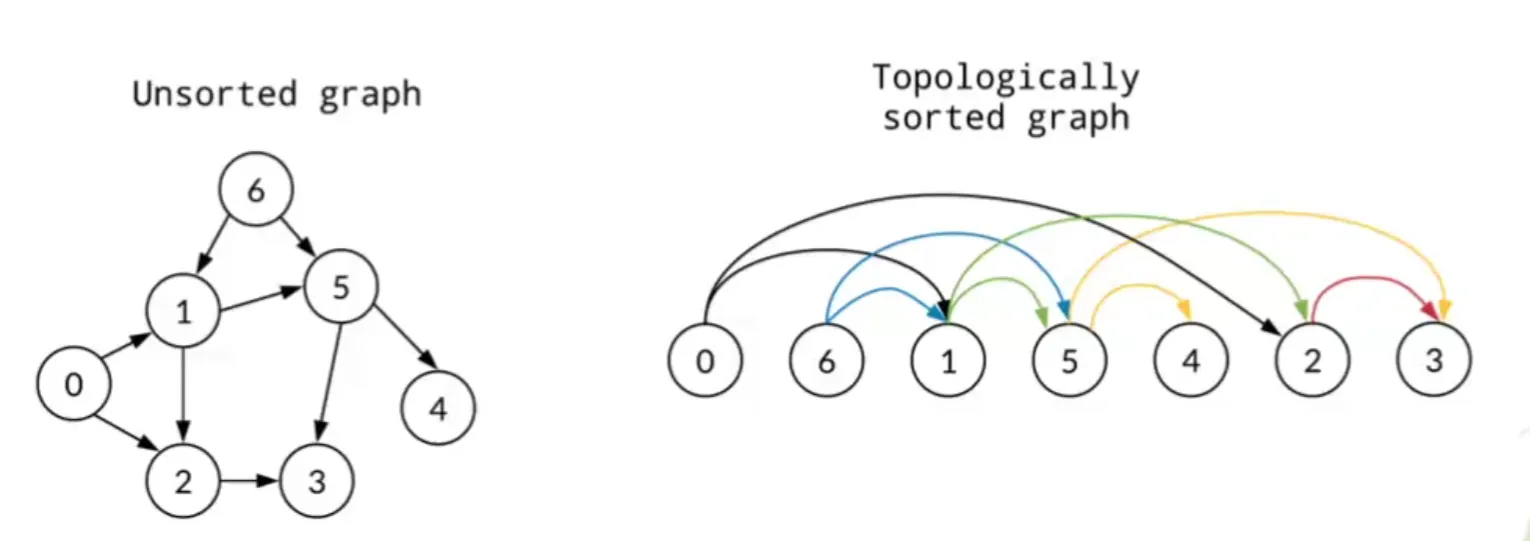
有向无环图可以称作拓扑图
拓扑序列 :所有的边都是从前指向后的。
并不是所有图都有拓扑序,有环就不行。
统计每个点的入度 将所有入度为 0 0 0 BFS(取出队头元素,遍历所有它的出边) 假设 t → j t\to{j} t → j
d j d_j d j j j j
入度为 0 0 0
所有入度为 0 0 0
所以第一步就是把所有入度为 0 0 0
然后取出队头,枚举出边。
然后删掉这条边(t → j t\to{j} t → j
就是 d [ j ] − 1 d[j]-1 d [ j ] − 1
假如入度为 0 0 0
如果有环
那么一定有一些点不会入队
如果一个图上并没有环
那么就可以把它拓扑掉
一个有向无环图一定有入度为0 0 0
反证法:
假如每个点的入度都不为0 0 0
那么一定可以沿着某个点无穷无尽的往上找
假如一共n n n
当找到第n + 1 n+1 n + 1
所以有向无环图至少存在一个入度为零的点
把它作为突破口
挖墙脚
加入队列的顺序就是拓扑序列
生成过程:
生成结果:
首先我们定义生成的边为树边,指向祖先的边称作回边,
遍历时遇到子树节点的边叫做前向边,遍历时遇到访问过的非祖先节点形成的边叫做横叉边。
观察这棵树,我们不难发现一些结论:
生成树中,回边连接的一定是子孙节点。如果连接的是兄弟节点,那么肯定会沿着这条“回边”继续 DFS 下去,那么这条回边将会成为树边,“兄弟”节点也不再是兄弟关系,而是子孙关系。 当树边 u → v u\to{v} u → v 回边一定不是桥。 假如无向连通图有桥,那么就不可能使每条边给定一个方向后成为一个强连通图。因为假定 u v uv u v u → v u\to{v} u → v v → u v\to{u} v → u 假如无向连通图无桥,那么就可以使每条边给定一个方向后成为一个强连通图,使树边均向下,回边均向上。 根节点可以移动到任意节点,任意节点都可以回到根节点。 回边和横叉边的终点时间戳一定大于起点。 对于每个强连通分量中的 dfs 生成树,必然存在一个点是其它所有点的祖先,即根节点 u u u v v v u u u u → v u\to{v} u → v v v v u u u
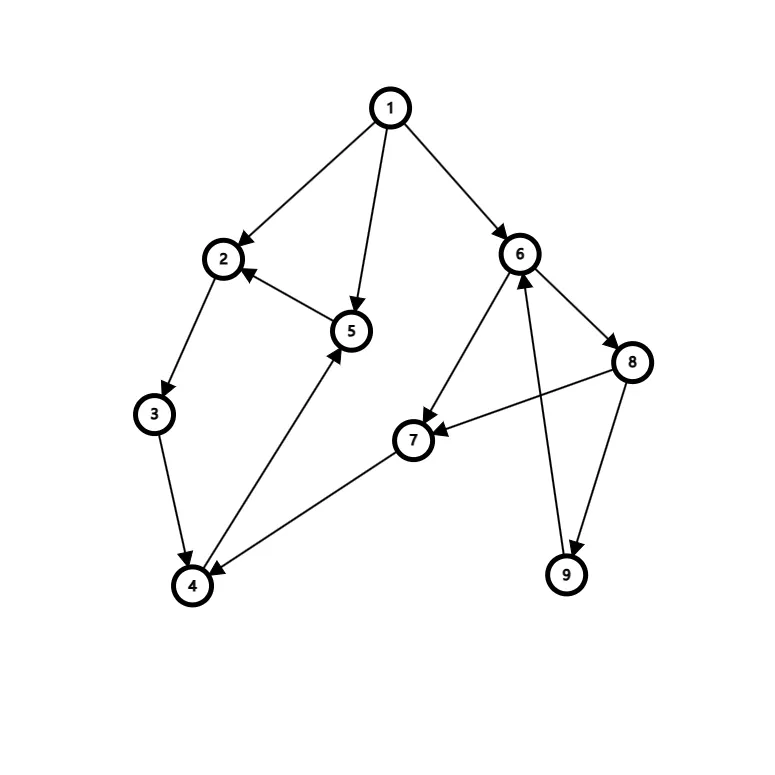
比如本图中5 → 2 5\to{2} 5 → 2 1 → 5 1\to{5} 1 → 5 3 → 4 3\to{4} 3 → 4
而改变一下 dfs 的顺序那么 dfs 生成树的形态将会不同。
比如上面两图。
仅改变了遍历顺序,生成的 dfs 树的形态便不同,每条边的性质也可能不同。
图解理解更佳
点的连通性:无向图中,若点 i i i j j j i i i j j j 连通图:无向图中,任意两点间均有路径。 连通分量:分量其实就是子图,特指无向图。无向图 的连通分量是它的最大连通子图 ,也就是说对于一个点蔓延出去的所有边,不能再往上加边了,而不是边数最多的连通子图,因此一个无向图可以有多个连通分量,连通分量 也叫做连通块 。也叫做极大连通分量 ,是一个概念。任何连通图的连通分量有且只有一个,即它本身。极小连通分量 是在保持连通性的前提下的最小子图,形态是一棵树。 强连通图:特指有向图 。有向图中,点 i i i j j j 强连通分量:有向图中的极大强连通子图。与上面类似的,极大强连通分量与极小连通分量。 生成树:连通图中包含所有顶点的极小连通子图。 桥:无向图中,若删除了一条边,整个图的连通分量发生了改变,那么这条边就是桥。桥其实就是连通各个连通块之间的唯一的边。 生成森林:即一个非连通图中,包含多个连通块,每个连通块的生成树所组成的集合。 有向图求 SCC
我们维护两个变量:
d f n i dfn_i d f n i i i i
l o w i low_i l o w i i i i
l o w ( p ) low(p) l o w ( p )
对于某个以 p p p p → q p\to{q} p → q
如果 q q q q q q p p p r r r q q q p p p p p p q q q q q q r r r q q q l o w ( p ) = min ( l o w ( p ) , l o w ( q ) ) low(p)=\min(low(p),low(q)) l o w ( p ) = min ( l o w ( p ) , l o w ( q ) )
如果 q q q p p p q q q l o w ( p ) = min ( l o w ( p ) , d f s n ( q ) ) low(p)=\min(low(p),dfsn(q)) l o w ( p ) = min ( l o w ( p ) , d f s n ( q ) )
强连通性不存在传递性。比如 u u u v v v v v v q q q u u u q q q u → v ← q u\rightarrow v \leftarrow q u → v ← q q q q d f s n dfsn d f s n p p p l o w low l o w
那么我怎么确定一个点是否可达呢?
因为回边和横叉边都指向 dfs 序较小的节点,而前向边又不影响上述转移方程,所以我们只需要确定哪些点比该点的 dfs 序小切能到达该点,这可以用一个栈来维护。
每次搜到新点就让它入栈,对点 p p p l o w ( p ) = n < d f s n ( p ) low(p)=n<dfsn(p) l o w ( p ) = n < d f s n ( p ) n n n q q q p p p q q q q q q p p p q q q p p p q q q p p p p p p p p p
也就是说,栈内的元素是当前搜索到的可能为强连通分量的元素,一个树在没有把它的若干子树搜索完全的情况下,之前搜索的树的子树不会出栈,出栈即意味着找到了一个强连通分量,当且仅当返回时发现l o w ( p ) = d f s n ( p ) low(p)=dfsn(p) l o w ( p ) = d f s n ( p )
显然,这样维护的栈内元素的 d f s n dfsn d f s n
每个点的 l o w ( ) low() l o w ( ) d f s n dfsn d f s n
我们实际上在找的每个节点的 l o w ( ) low() l o w ( ) d f s n dfsn d f s n
一个点的子树搜索完毕时,它的 l o w ( ) low() l o w ( )
得到的强连通分量编号的顺序符合拓扑序(编号越小,拓扑序越靠后)。
把每个强连通分量缩为一个点之后,得到的是一张有向无环图 ,因为只要能遍历到其中一个点,就一定能遍历到该强连通分量的所有点。
强连通分量中 ,tarjan 关注的是在不在一个强连通分量内 。
而割点割边 问题中关注搜索子树的个数 。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> using namespace std;const int N=1e5 +7 ;stack<int > s; vector<int > g[N]; vector<int > g_2[N]; int dfsn[N],low[N],ins[N],scc[N],deep,cscc,n;void tarjan (int p) low[p]=dfsn[p]=++deep; ins[p]=1 ; s.push (p); for (auto &q:g[p]) { if (!dfsn[q]) { tarjan (q); low[p]=min (low[p],low[q]); } else if (ins[q]) low[p]=min (low[p],dfsn[q]); } if (low[p]==dfsn[p]) { int top=0 ; cscc++; while (top!=p) { top=s.top (); s.pop (); ins[top]=0 ; scc[top]=cscc; } } } int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) if (!dfsn[i]) tarjan (i); for (int i=1 ;i<=n;i++) for (auto j:g[i]) if (scc[i]!=scc[j]) g_2[scc[i]].push_back (scc[j]); return 0 ; }
重边与自环对于有向图求强连通分量来说没有影响。
无向图
首先我们来明确一下这两个概念的定义:
割点:删去这个点会使无向图的连通分量数增加。 桥(割边):删去这条边会使无向图的连通分量数增加。 那么我总不能把每条边和每个点都删掉看看吧,这样肯定行不通。
如何求割点与割边?
在无向图中,l o w low l o w
无向图中,只需要考虑回边,因为无向图的 dfs 树不存在横叉边和前向边。
设以 p p p s u b t r e e ( p ) subtree(p) s u b t r e e ( p ) l o w ( p ) low(p) l o w ( p ) s u b t r e e ( p ) subtree(p) s u b t r e e ( p ) s u b t r e e ( p ) subtree(p) s u b t r e e ( p ) d f s n dfsn d f s n
若 p p p q q q l o w ( q ) ≥ d f s n ( p ) low(q)\ge{dfsn(p)} l o w ( q ) ≥ d f s n ( p ) q q q 逃 到比 p p p q q q 逃 出去,只能通过它的父亲节点也就是 p p p p p p q q q d f s n dfsn d f s n p p p p p p
那q q q
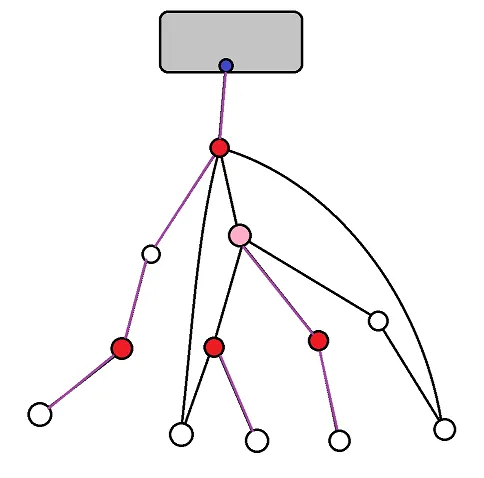
这样一张图,有颜色的都是割点/割边(注:左边从下往上第三个点应该也是割点)。
很明显割点的父亲或儿子不一定也是割点。
两个割点之间也不一定是割边。
割边的两端也不一定是割点。
这里引入一个结论:割边两端点都是割点当且仅当去掉这条割边后得到的连通块大小都 ≥ 2 \ge{2} ≥ 2
所以重复一遍:p p p q q q l o w ( q ) ≥ d f s n ( p ) low(q)\ge{dfsn(p)} l o w ( q ) ≥ d f s n ( p ) p p p
还有一种特殊情况,当 p p p p p p
因此对于根节点 ,若有两个以上子节点,那就是割点。
P3388 割点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;const int N=1e6 +7 ;vector<int > e[N]; int dfsn[N],low[N];int cnt;vector<int > point; void tarjan (int p,bool root=true ) int tot=0 ; low[p]=dfsn[p]=++cnt; for (auto &q:e[p]) { if (!dfsn[q]) { tarjan (q,false ); low[p]=min (low[p],low[q]); tot+=(low[q]>=dfsn[p]); } else { low[p]=min (low[p],dfsn[q]); } } if (tot>root) point.push_back (p); } int main () int n,m; scanf ("%d%d" ,&n,&m); }
割边,也叫做桥,定义之前说过。
较割点,修改一下l o w low l o w
经过以自身为根节点的子树中至多一条非树边能够到达的最小 dfs 序的点,其中非树边不包括儿子到父亲的反向边 。 所以对于l o w q > d f n p low_q>dfn_p l o w q > d f n p p ↔ q p\leftrightarrow{q} p ↔ q
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <bits/stdc++.h> using namespace std;const int N=1e6 +7 ;vector<int > e[N]; int dfsn[N],low[N],fa[N];int cnt;vector<int > point; void tarjan_0 (int p) low[p]=dfsn[p]=++cnt; for (auto &q:e[p]) { if (!dfsn[q]) { fa[q]=p; tarjan_0 (q); low[p]=min (low[p],low[q]); if (low[q]>dfsn[p]) bridges.emplace_back (p,q); } else if (fa[p]!=q) low[p]=min (low[p],dfsn[q]); } } int main () int n,m; scanf ("%d%d" ,&n,&m); }
它和割点的区别在于它不能到它的父亲。
v-DCC
是满足图中不包含任意割点的极大连通子图。
即删去任何一个点不会使这个图的连通性发生改变。
一个孤立的点是一个点双连通分量,两个割点是一个点双连通分量。
对于自环,我们特判掉即可,实际上也是一个孤立点。
对于不同的两个点双之间有且只有一个公共点,且这个点就是割点。
假如有多个公共点,那么删除任意一个公共点,两个点双之间还是可以相互连通,那么它们就可以合并为一个大的点双,因此有以上结论。
所以我们求点双连通分量也就是求每个割点的子树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 #include <iostream> #include <vector> #include <stack> using namespace std;const int N = 5e5 + 10 ;const int M = 2e6 + 7 ;int n, m, edcnt, cnt, cdcc;int fir[N], low[N], dfsn[N];vector<int > dcc[N]; vector<int > point; stack<int > s; struct Edge { int to, nxt; }e[M << 1 ]; void add (int u, int v) e[++edcnt].to = v; e[edcnt].nxt = fir[u]; fir[u] = edcnt; } void tarjan (int p, bool root = true ) int tot = 0 ; dfsn[p] = low[p] = ++cnt; s.push (p); if (root && fir[p] == 0 ) { dcc[++cdcc].emplace_back (p); return ; } for (int i = fir[p]; i; i = e[i].nxt) { int q = e[i].to; if (!dfsn[q]) { tarjan (q, false ); low[p] = min (low[p], low[q]); if (low[q] >= dfsn[p]) { tot++; if (tot > root) point.push_back (p); cdcc++; int top = 0 ; while (top != q) { top = s.top (); s.pop (); dcc[cdcc].emplace_back (top); } dcc[cdcc].emplace_back (p); } } else low[p] = min (low[p], dfsn[q]); } } int main () scanf ("%d%d" , &n, &m); for (int i = 1 ; i <= m; i++) { int u, v; scanf ("%d%d" , &u, &v); if (u == v) continue ; add (u, v); add (v, u); } for (int i = 1 ; i <= n; i++) if (!dfsn[i]) tarjan (i); printf ("%d\n" , cdcc); for (int i = 1 ; i <= cdcc; i++) { printf ("%d" , (int )dcc[i].size ()); for (auto &j : dcc[i]) printf (" %d" , j); puts ("" ); } return 0 ; }
e-DCC
与点双类似,即不含割边的最大子图。
但是这个是不能通过反向边回到父亲,而重边其实属于非树边是可以走的,因此不可以通过判 f a fa f a
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 #include <iostream> #include <vector> #include <stack> using namespace std;const int N = 5e5 + 7 , M = 2e6 + 7 ;int n, m, cnt, edcnt = 1 , cdcc;vector<int > dcc[N]; stack<int > s; int fir[N], low[N], dfsn[N];struct Edge { int to, nxt; }e[M << 1 ]; void add (int u, int v) e[++edcnt].to = v; e[edcnt].nxt = fir[u]; fir[u] = edcnt; } void tarjan (int p, int f) low[p] = dfsn[p] = ++cnt; s.push (p); for (int i = fir[p]; i; i = e[i].nxt) { int q = e[i].to; if (!dfsn[q]) { tarjan (q, i); low[p] = min (low[p], low[q]); } else if (i != (f ^ 1 )) low[p] = min (low[p], dfsn[q]); } if (low[p] == dfsn[p]) { int top = 0 ; cdcc++; while (top != p) { top = s.top (); s.pop (); dcc[cdcc].emplace_back (top); } } } int main () scanf ("%d%d" , &n, &m); for (int i = 1 ; i <= m; i++) { int u, v; scanf ("%d%d" , &u, &v); if (u == v) continue ; add (u, v); add (v, u); } for (int i = 1 ; i <= n; i++) if (!dfsn[i]) tarjan (i, -1 ); printf ("%d\n" , cdcc); for (int i = 1 ; i <= cdcc; i++) { printf ("%d" , (int )dcc[i].size ()); for (auto &j : dcc[i]) { printf (" %d" , j); } puts ("" ); } return 0 ; }
用在一条边上是最优的
枚举每条边,看看把所有花费都用在它身上能降低多少代价
如果是树边,那么直接减去
如果非树边,那就和链上最大值作差,使差值最大(也就是减小地最大)
先求生成树中白色边最少有多少条
其次算生成树中白色边最多有多少条
也就是白边优先跑一遍 Kruscal
再黑边优先跑一边 Kruscal
如果存在一个斐波那契数处于这个最大值和最小值的区间内
那么就存在这样一颗生成树
否则不存在
因为白边最小到白边最多的过程就是一条条把黑边替换成白边的过程
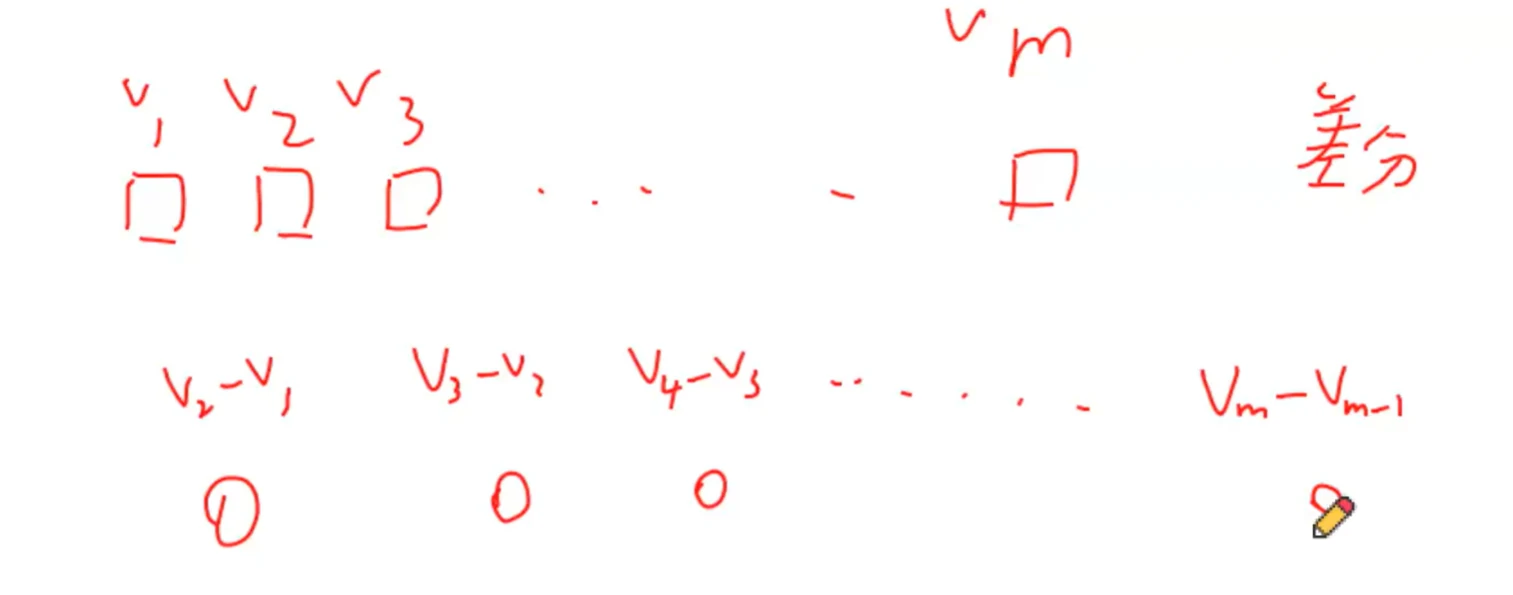
使它们差分序列= 0 =0 = 0
让这m m m
在差分序列 中体现为前面的某个值加上x,后面的某个值减去x
在这段差分序列中,和是不变的
如果是有解的,那么首先要保证这m m m 0 0 0