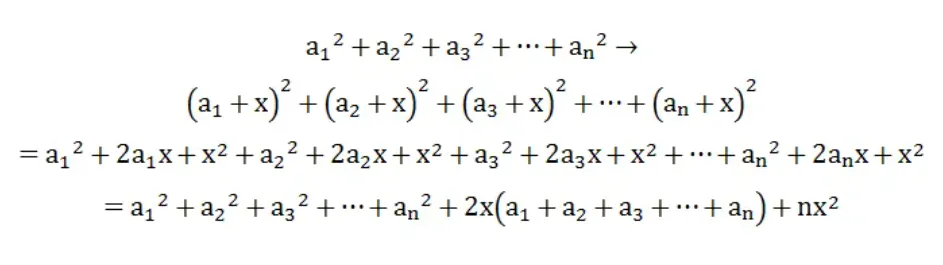也没有很杂
分两种情况讨论:
如果删去的这个点不是割点,那么有序点对的数不变,连通分量只有两个,分别是这个点和剩下的所有点,答案是2 × ( n − 1 ) 2\times(n-1) 2 × ( n − 1 ) 如果删去的这个点是割点,那么这张连通图将会变为若干连通分量,分别是这个点、这个点的若干个子树,以及剩下的所有点。设s i z i siz_i s i z i i i i s u m sum s u m i i i ∑ i s i z i × ( n − s i z i ) + 1 × ( n − 1 ) + ( n − s u m − 1 ) × ( s u m + 1 ) \sum_i{siz_i\times(n-siz_i)}+1\times(n-1)+(n-sum-1)\times(sum+1) ∑ i s i z i × ( n − s i z i ) + 1 × ( n − 1 ) + ( n − s u m − 1 ) × ( s u m + 1 ) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 #include <bits/stdc++.h> using namespace std;const int N=1e5 +10 ;const int M=5e5 +10 ;int n,m,edcnt,cnt;int fir[N],dfsn[N],low[N],siz[N];long long ans[N];bool cut[N];struct edge { int to,nxt; }e[M<<1 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void tarjan (int p) int tot=0 ,sum=0 ; dfsn[p]=low[p]=++cnt; siz[p]=1 ; for (int i=fir[p];i;i=e[i].nxt) { int q=e[i].to; if (!dfsn[q]) { tarjan (q); siz[p]+=siz[q]; low[p]=min (low[p],low[q]); if (low[q]>=dfsn[p]) { ans[p]+=1ll *siz[q]*(n-siz[q]); sum+=siz[q]; tot++; if (p!=1 ||tot>1 ) cut[p]=true ; } } else low[p]=min (low[p],dfsn[q]); } if (!cut[p]) ans[p]=2 *(n-1 ); else ans[p]+=(n-1 )*1 +1ll *(n-sum-1 )*(sum+1 ); } int main () scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=m;i++) { int u,v; scanf ("%d%d" ,&u,&v); add (u,v); add (v,u); } tarjan (1 ); for (int i=1 ;i<=n;i++) printf ("%lld\n" ,ans[i]); return 0 ; }
先求一下边双连通分量,然后对边双连通分量进行缩点,然后就可以找到度数为1的节点,答案就是⌈ s 2 ⌉ \lceil\frac{s}{2}\rceil ⌈ 2 s ⌉
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 #include <bits/stdc++.h> using namespace std;const int N=5050 ;const int M=2e4 +10 ;int n,m,edcnt,cnt,cdcc,ans;map<int ,bool > bj[N]; int fir[N],low[N],fa[N],dfsn[N],dcc[N],dd[N];stack<int > s; struct edge { int to,nxt; }e[M]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void tarjan (int p) dfsn[p]=low[p]=++cnt; s.push (p); for (int i=fir[p];i;i=e[i].nxt) { int q=e[i].to; if (!dfsn[q]) { fa[q]=p; tarjan (q); low[p]=min (low[p],low[q]); } else if (fa[p]!=q) low[p]=min (low[p],dfsn[q]); } if (dfsn[p]==low[p]) { cdcc++; int top; do { top=s.top (); s.pop (); dcc[top]=cdcc; } while (top!=p); } } int main () scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=m;i++) { int u,v; scanf ("%d%d" ,&u,&v); if (bj[u][v]||bj[v][u]) continue ; add (u,v); add (v,u); bj[u][v]=true ; bj[v][u]=true ; } tarjan (1 ); for (int i=1 ;i<=edcnt;i+=2 ) { int x=e[i].to; int y=e[i+1 ].to; if (dcc[x]!=dcc[y]) dd[dcc[x]]++,dd[dcc[y]]++; } for (int i=1 ;i<=cdcc;i++) if (dd[i]==1 ) ans++; printf ("%d" ,(ans+1 )/2 ); return 0 ; }
记得判重边!
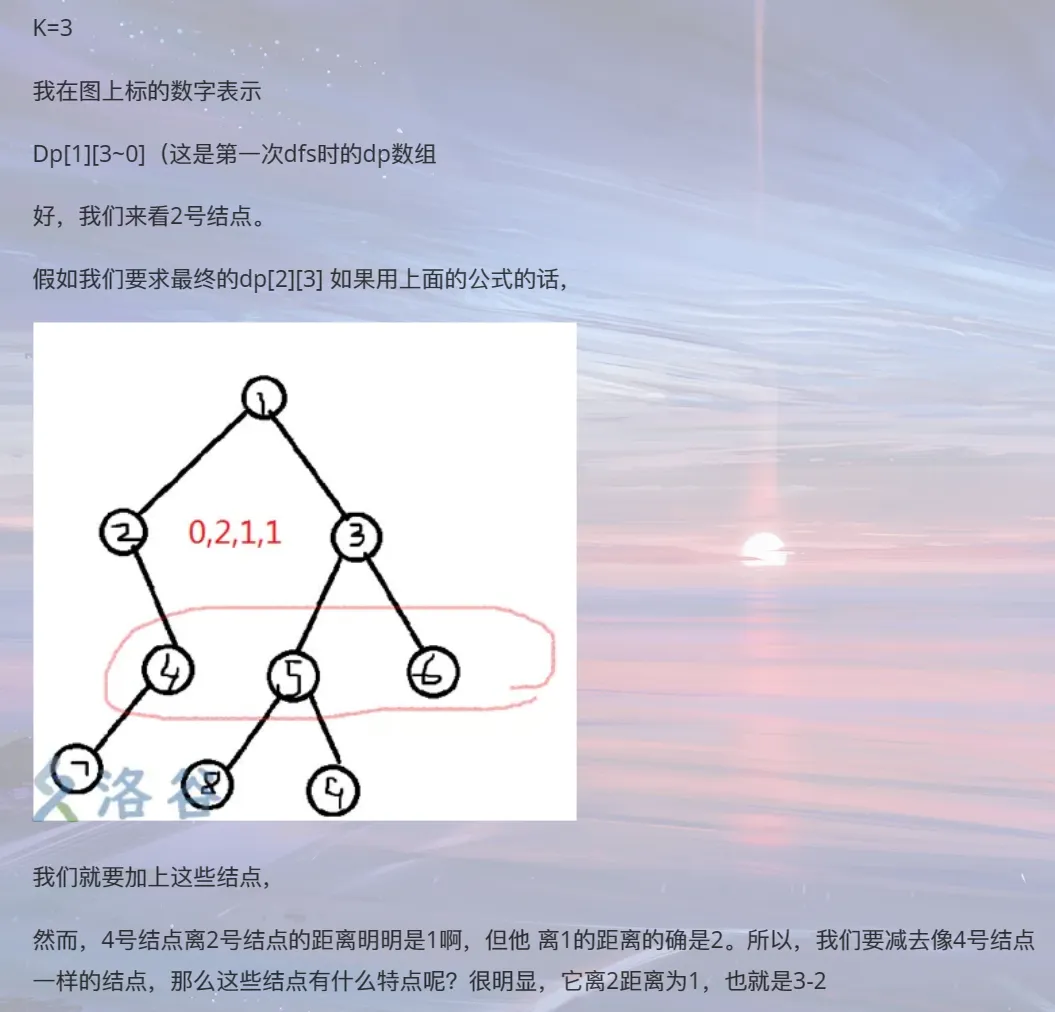
点双连通分量的缩点,然后利用LCA求距离,x x x y y y d e p t h x + d e p t h y − 2 × d e p t h l c a ( x , y ) depth_x+depth_y-2\times{depth_{lca(x,y)}} d e p t h x + d e p t h y − 2 × d e p t h l c a ( x , y )
由于是碳的个数,所以还需要加一。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 #include <bits/stdc++.h> using namespace std;const int N=1e4 +10 ;const int M=5e4 +10 ;int n,m,cdcc,q;int low[N],dfsn[N],cnt,edcnt;int fir[N],fa[N];int dcc[N],depth[N],f[N][23 ];int a[100 ];map<int ,bool > bj[N]; vector<int > mp[N]; stack<int > s; struct edge { int to,nxt; }e[M<<1 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void tarjan (int p) low[p]=dfsn[p]=++cnt; s.push (p); for (int i=fir[p];i;i=e[i].nxt) { int v=e[i].to; if (!dfsn[v]) { fa[v]=p; tarjan (v); low[p]=min (low[p],low[v]); } else if (v!=fa[p]) low[p]=min (low[p],dfsn[v]); } if (dfsn[p]==low[p]) { cdcc++; int top; do { top=s.top (); s.pop (); dcc[top]=cdcc; } while (top!=p); } } void dfs (int u) for (auto &v:mp[u]) if (v!=f[u][0 ]) { depth[v]=depth[u]+1 ; f[v][0 ]=u; for (int i=1 ;i<=21 ;i++) f[v][i]=f[f[v][i-1 ]][i-1 ]; dfs (v); } } int lca (int x,int y) if (depth[x]<depth[y]) swap (x,y); for (int i=21 ;i>=0 ;i--) if (depth[f[x][i]]>=depth[y]) x=f[x][i]; if (x==y) return x; for (int i=21 ;i>=0 ;i--) { int nx=f[x][i]; int ny=f[y][i]; if (nx!=ny) { x=nx; y=ny; } } return f[x][0 ]; } int dist (int x,int y) int l=lca (x,y); return depth[x]+depth[y]-2 *depth[l]; } int main () scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=m;i++) { int u,v; scanf ("%d%d" ,&u,&v); if (u==v) continue ; if (bj[u][v]||bj[v][u]) continue ; bj[u][v]=true ; bj[v][u]=true ; add (u,v); add (v,u); } tarjan (1 ); for (int i=1 ;i<=n;i++) for (int j=fir[i];j;j=e[j].nxt) { int v=e[j].to; if (dcc[i]!=dcc[v]) mp[dcc[i]].push_back (dcc[v]); } depth[0 ]=-1 ; dfs (1 ); scanf ("%d" ,&q); for (int i=1 ;i<=q;i++) { int x,y; scanf ("%d%d" ,&x,&y); int ans=dist (dcc[x],dcc[y])+1 ; int j=0 ; while (ans>0 ) { a[j]=ans&1 ; j++; ans>>=1 ; } for (j--;j>=0 ;j--) printf ("%d" ,a[j]); puts ("" ); } return 0 ; }
左下对角线的横纵坐标之和不变,右下对角线的横纵坐标之差不变,作差要记得加上 n n n
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <bits/stdc++.h> using namespace std;const int N = 3e5 +7 ;int n,tot;bool line[N], ldia[N], rdia[N];int row[N];void Dfs (int x) if (x > n) { tot++; if (tot > 3 ) return ; for (int i = 1 ; i <= n; i++) printf ("%d " , row[i]); puts ("" ); return ; } for (int i = 1 ; i <= n; ++i) { if (!(line[i]) && (!ldia[x + i]) && (!rdia[x - i +n])) { row[x] = i; line[i] = true ; ldia[x + i] = true ; rdia[x + n - i] = true ; Dfs (x + 1 ); line[i] = false ; ldia[x + i] = false ; rdia[x + n - i] = false ; } } } int main () scanf ("%d" , &n); Dfs (1 ); printf ("%d\n" , tot); return 0 ; }
注释。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <bits/stdc++.h> using namespace std;const int N = 22 ;string s[N]; int used[N],length = 0 , n;int Link (string s1, string s2) int len = min (s1.l ength(), s2.l ength()); for (int i = 1 ; i < len; ++i) { bool bj = true ; for (int j = 0 ; j < i; ++j) if (s1[s1.l ength() - i + j] != s2[j]) bj = false ; if (bj) return i; } return 0 ; } void Dfs (string now, int len) length = max (len, length); for (int i = 0 ; i < n; ++i) { if (used[i] >= 2 ) continue ; int over = Link (now, s[i]); if (over > 0 ) { used[i]++; Dfs (s[i], len + s[i].length () - over); used[i]--; } } } int main () scanf ("%d" , &n); for (int i = 0 ; i <= n; ++i) cin >> s[i]; Dfs (' ' + s[n], 1 ); printf ("%d" , length); return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <bits/stdc++.h> using namespace std;const int N = 1005 ;typedef long long ll;int n, c;ll ans = -1 ; int w[N];ll pre[N]; bool vis[N];void Dfs (int x, ll sum) if (sum > c) return ; if (pre[x - 1 ] + sum <= c) { ans = max (ans, pre[x - 1 ] + sum); return ; } ans = max (ans, sum); for (int i = x - 1 ; i >= 1 ; --i) Dfs (i, sum + w[i]); return ; } int main () scanf ("%d%d" , &n, &c); for (int i = 1 ; i <= n; ++i) { scanf ("%d" , &w[i]); pre[i] = pre[i - 1 ] + w[i]; } Dfs (n + 1 , 0 ); printf ("%lld" , ans); return 0 ; }
树上两条路径有交点,路径分别为a ↔ b a\leftrightarrow{b} a ↔ b c ↔ d c\leftrightarrow{d} c ↔ d l c a ( a , b ) lca(a,b) l c a ( a , b ) c , d c,d c , d l c a ( c , d ) lca(c,d) l c a ( c , d ) a , b a,b a , b
判断一个点是否在一个路径上,可以判断这个点到左右端点的距离之和是否等于做右端点的距离,而处理两点之间距离可以通过l c a lca l c a
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 #include <bits/stdc++.h> using namespace std;int n,q,edcnt;const int N=2e5 +9 ;int fir[N],depth[N],f[N][23 ];struct edge { int to,nxt; }e[N]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void init (int u) for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=f[u][0 ]) { int v=e[i].to; depth[v]=depth[u]+1 ; f[v][0 ]=u; for (int i=1 ;i<=21 ;i++) f[v][i]=f[f[v][i-1 ]][i-1 ]; init (v); } } int lca (int p1,int p2) if (depth[p1]<depth[p2]) swap (p1,p2); for (int i=21 ;i>=0 ;i--) { if (depth[f[p1][i]]>=depth[p2]) p1=f[p1][i]; } if (p1==p2) return p1; for (int i=21 ;i>=0 ;i--) { if (f[p1][i]!=f[p2][i]) p1=f[p1][i],p2=f[p2][i]; } return f[p1][0 ]; } int dist (int x,int y) int l=lca (x,y); return depth[x]+depth[y]-2 *depth[l]; } int main () scanf ("%d%d" ,&n,&q); for (int i=1 ;i<=n-1 ;i++) { int u,v; scanf ("%d%d" ,&u,&v); add (u,v); add (v,u); } init (1 ); for (int i=1 ;i<=q;i++) { int a,b,c,d; scanf ("%d%d%d%d" ,&a,&b,&c,&d); int lab=lca (a,b),lcd=lca (c,d); if (dist (c,lab)+dist (d,lab)==dist (c,d)||dist (a,lcd)+dist (b,lcd)==dist (a,b)) printf ("Y\n" ); else printf ("N\n" ); } return 0 ; }
首先,这是棵树,最坏情况下两个朋友的家正好是树的直径的两个端点,然后我们枚举一下树上每个点(不包含直径端点),看下这个点到两个端点之间距离的最小值最大即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 #include <bits/stdc++.h> using namespace std;const int N=2e5 +10 ;typedef long long ll;int n,m,edcnt;ll ans; struct edge { int nxt,to,val; }e[N<<1 ]; int fir[N];int F,G;void add (int u,int v,int w) e[++edcnt].to=v; e[edcnt].val=w; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } int df[N][23 ],depth[N];ll d[N]; void dfs (int u,int fa) for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; df[v][0 ]=u; depth[v]=depth[u]+1 ; d[v]=d[u]+e[i].val; for (int j=1 ;j<=22 ;j++) df[v][j]=df[df[v][j-1 ]][j-1 ]; dfs (v,u); } } int lca (int x,int y) depth[0 ]=-1 ; if (depth[x]<depth[y]) swap (x,y); for (int i=22 ;i>=0 ;i--) if (depth[df[x][i]]>=depth[y]) x=df[x][i]; if (x==y) return x; for (int i=22 ;i>=0 ;i--) if (df[x][i]!=df[y][i]) x=df[x][i],y=df[y][i]; return df[x][0 ]; } ll dist (int x,int y) return d[x]+d[y]-2 *d[lca (x,y)]; } void dfs1 (int u,int fa,ll sum) if (sum>=ans) { ans=sum; F=u; } for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) dfs1 (e[i].to,u,sum+e[i].val); } void dfs2 (int u,int fa,ll sum) if (sum>=ans) { ans=sum; G=u; } for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) dfs2 (e[i].to,u,sum+e[i].val); } int main () scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=m;i++) { int u,v,w; scanf ("%d%d%d" ,&u,&v,&w); add (u,v,w); add (v,u,w); } dfs (1 ,-1 ); dfs1 (1 ,-1 ,0 ); ans=-1 ; dfs2 (F,-1 ,0 ); ans=-1 ; ll len=dist (F,G); for (int i=1 ;i<=n;i++) if (i!=F&&i!=G) ans=max (ans,min (dist (i,F),dist (i,G))); printf ("%lld" ,ans+len); return 0 ; }
这道题首先 DFS 两遍求出直径以及直径的两个端点,然后再 DFS 一遍找到直径的路径,然后标记这条路径上的每一条边,然后再分别进行两次 DFS,这个过程中记录每个点以A/B 为根节点时,到子树中非直径的最长路径,如果这个最长路径等与该点到对应直径端点的距离的话,那么就出现了分叉,这时候就可以被替代,所以这个点下面就不再是所有直径的公共边,就这样不断向内缩,从一端缩完再缩另一端,剩下的就是公共边。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 #include <bits/stdc++.h> using namespace std;const int N=200010 ;typedef long long ll;int n,edcnt=1 ;int A,B;ll dist_AB,flen_A[N],flen_B[N],lins,length[N]; int fir[N],depth[N],f[N][25 ];int line[N],cnt;bool bj;bool vis[N<<1 ];vector<int > point; struct edge { int to,nxt,val; }e[N<<1 ]; void add (int u,int v,int w) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; e[edcnt].val=w; fir[u]=edcnt; } int lca (int x,int y) depth[0 ]=-1 ; if (depth[x]<depth[y]) swap (x,y); for (int i=23 ;i>=0 ;i--) if (depth[f[x][i]]>=depth[y]) x=f[x][i]; if (x==y) return x; for (int i=23 ;i>=0 ;i--) if (f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0 ]; } int dist_1 (int x,int y) return depth[x]+depth[y]-2 *depth[lca (x,y)]; } ll dist_2 (int x,int y) return length[x]+length[y]-2 *length[lca (x,y)]; } void dfs (int u,int fa,ll sum,int first) if (sum>lins&&first<=1 ) { lins=sum; if (first==0 ) A=u; if (first==1 ) B=u,dist_AB=sum; } for (int i=fir[u];i;i=e[i].nxt) { int v=e[i].to; if (v==fa) continue ; if (first==0 ) { depth[v]=depth[u]+1 ; length[v]=length[u]+e[i].val; f[v][0 ]=u; for (int i=1 ;i<=23 ;i++) f[v][i]=f[f[v][i-1 ]][i-1 ]; } dfs (v,u,sum+e[i].val,first); if (first==3 &&vis[i]==false ) flen_A[u]=max (flen_A[u],flen_A[v]+e[i].val); if (first==4 &&vis[i]==false ) flen_B[u]=max (flen_B[u],flen_B[v]+e[i].val); } } void dfs_again (int u,int fa) if (u==B) { point.emplace_back (u); bj=true ; return ; } for (int i=fir[u];i;i=e[i].nxt) { int v=e[i].to; if (v==fa) continue ; dfs_again (v,u); if (bj) { vis[i]=vis[i^1 ]=true ; point.emplace_back (u); return ; } } } int main () scanf ("%d" ,&n); int u,v,w; for (int i=1 ;i<=n-1 ;i++) { scanf ("%d%d%d" ,&u,&v,&w); add (u,v,w); add (v,u,w); } dfs (u,-1 ,0 ,0 ); lins=0 ; dfs (A,-1 ,0 ,1 ); dfs_again (A,-1 ); dfs (A,-1 ,0 ,3 ); dfs (B,-1 ,0 ,4 ); int ans1=dist_1 (A,B); for (auto &i:point) line[++cnt]=i; for (int i=1 ;i<=cnt;i++) if (dist_2 (line[i],A)==flen_B[line[i]]) { ans1-=dist_1 (A,line[i]); break ; } for (int j=cnt;j>=1 ;j--) { if (dist_2 (line[j],B)==flen_A[line[j]]) { ans1-=dist_1 (B,line[j]); break ; } } printf ("%lld\n%d" ,dist_AB,ans1); return 0 ; }
P8655
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 #include <bits/stdc++.h> using namespace std;const int N=1e5 +7 ;int n,edcnt;struct edge { int to,nxt; }e[N<<1 ]; int fir[N];bool vis[N];bool bj;int st;int ans[N];int cnt;vector<int > mp; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void dfs (int u,int fa) for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; if (vis[v]) { mp.push_back (v); st=v; bj=true ; return ; } vis[v]=true ; dfs (v,u); if (bj) { if (v==st) { st=0 ; } if (st) { mp.push_back (v); } return ; } vis[v]=false ; } } int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) { int u,v; scanf ("%d%d" ,&u,&v); add (u,v); add (v,u); } vis[1 ]=true ; dfs (1 ,-1 ); for (auto &i:mp) ans[++cnt]=i; sort (ans+1 ,ans+cnt+1 ); for (int i=1 ;i<=cnt;i++) printf ("%d " ,ans[i]); return 0 ; }
首先先找环把这个环的两个端点和连接两个端点的边找出,在树形DP的时候注意两个端点不能同时选即可,由于是环,所以要对两个端点分别进行DP。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 #include <bits/stdc++.h> using namespace std;const int N=1e6 +7 ;typedef long long ll;int n,edcnt=1 ;struct edge { int to,nxt; }e[N<<1 ]; int fir[N];bool vis[N];int A,B,E;ll ans; ll f[N][2 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } int battleEffectiveness[N];void Find (int u,int fa) vis[u]=true ; for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; if (vis[v]) { A=u; B=v; E=i; continue ; } Find (v,u); } } void dp (int u,int fa) f[u][0 ]=0 ; f[u][1 ]=battleEffectiveness[u]; for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa&&i!=E&&(i^1 )!=E) { int v=e[i].to; dp (v,u); f[u][0 ]+=max (f[v][0 ],f[v][1 ]); f[u][1 ]+=f[v][0 ]; } } int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) { int hate; scanf ("%d%d" ,&battleEffectiveness[i],&hate); add (i,hate); add (hate,i); } for (int i=1 ;i<=n;i++) { if (vis[i]) continue ; Find (i,-1 ); dp (A,-1 ); ll temp=f[A][0 ]; dp (B,-1 ); temp=max (temp,f[B][0 ]); ans+=temp; } printf ("%lld" ,ans); return 0 ; }
将横坐标从小到大排序,而纵坐标由于是实数所以需要对它的下标进行离散化,线段树的一个节点代表一个区间,n个数那么就有n − 1 n-1 n − 1 n − 1 n-1 n − 1 1 ∼ s i z − 1 1\sim{siz-1} 1 ∼ s i z − 1 0 ∼ s i z − 2 0\sim{siz-2} 0 ∼ s i z − 2
面积就按x轴从左往右扫描线,每块面积相加即可。
c n t cnt c n t l e n len l e n
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 #include <bits/stdc++.h> using namespace std;const int N=1e5 +10 ;int n;struct segment { double x,y1,y2; int k; bool operator <(const segment &a)const { return x<a.x; } }seg[N<<1 ]; struct node { int l,r; int cnt; double len; }tr[N<<3 ]; vector<double > ys; int find (double y) return lower_bound (ys.begin (),ys.end (),y)-ys.begin (); } void pushup (int u) if (tr[u].cnt) tr[u].len=(ys[tr[u].r+1 ]-ys[tr[u].l]); else if (tr[u].l!=tr[u].r) tr[u].len=tr[u<<1 ].len+tr[u<<1 |1 ].len; else tr[u].len=0 ; } void build (int u,int l,int r) tr[u].l=l,tr[u].r=r; if (l==r) { tr[u].len=0 ,tr[u].cnt=0 ; return ; } int mid=(l+r)>>1 ; build (u<<1 ,l,mid),build (u<<1 |1 ,mid+1 ,r); } void modify (int u,int l,int r,int v) if (tr[u].l>=l&&tr[u].r<=r) { tr[u].cnt+=v; pushup (u); return ; } int mid=(tr[u].l+tr[u].r)>>1 ; if (l<=mid) modify (u<<1 ,l,r,v); if (r>mid) modify (u<<1 |1 ,l,r,v); pushup (u); } int main () int t=1 ; while (scanf ("%d" ,&n),n) { ys.clear (); for (int i=1 ,j=0 ;i<=n;i++) { double x1,x2,y1,y2; scanf ("%lf%lf%lf%lf" ,&x1,&y1,&x2,&y2); seg[j++]={x1,y1,y2,1 }; seg[j++]={x2,y1,y2,-1 }; ys.push_back (y1),ys.push_back (y2); } sort (ys.begin (),ys.end ()); ys.erase (unique (ys.begin (),ys.end ()),ys.end ()); sort (seg,seg+n*2 ); build (1 ,0 ,(int )ys.size ()-2 ); double res=0 ; for (int i=0 ;i<n*2 ;i++) { if (i>0 ) res+=tr[1 ].len*(seg[i].x-seg[i-1 ].x); modify (1 ,find (seg[i].y1),find (seg[i].y2)-1 ,seg[i].k); } printf ("Test case #%d\n" ,t++); printf ("Total explored area: %.2lf\n\n" ,res); } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 #include <bits/stdc++.h> using namespace std;typedef long long ll;const int N=1e5 +7 ;int n;struct segment { int x,y1,y2,k; bool operator <(const segment &a)const { return x<a.x; } }seg[N<<1 ]; struct node { int l,r; int len,cnt; }tr[N<<3 ]; vector<int > mem; int find (int x) return lower_bound (mem.begin (),mem.end (),x)-mem.begin (); } void build (int u,int l,int r) tr[u].l=l,tr[u].r=r; if (tr[u].l==tr[u].r) { tr[u].len=tr[u].cnt=0 ; return ; } int mid=(l+r)>>1 ; build (u<<1 ,l,mid); build (u<<1 |1 ,mid+1 ,r); } void pushup (int u) if (tr[u].cnt) tr[u].len=mem[tr[u].r+1 ]-mem[tr[u].l]; else if (tr[u].l!=tr[u].r) tr[u].len=tr[u<<1 ].len+tr[u<<1 |1 ].len; else tr[u].len=0 ; } void modify (int u,int l,int r,int v) if (tr[u].l>=l&&tr[u].r<=r) { tr[u].cnt+=v; pushup (u); return ; } int mid=(tr[u].l+tr[u].r)>>1 ; if (l<=mid) modify (u<<1 ,l,r,v); if (r>mid) modify (u<<1 |1 ,l,r,v); pushup (u); } int main () scanf ("%d" ,&n); for (int i=1 ,j=0 ;i<=n;i++) { int x1,y1,x2,y2; scanf ("%d%d%d%d" ,&x1,&y1,&x2,&y2); seg[j++]={x1,y1,y2,1 }; seg[j++]={x2,y1,y2,-1 }; mem.push_back (y1),mem.push_back (y2); } build (1 ,0 ,mem.size ()-2 ); sort (mem.begin (),mem.end ()); mem.erase (unique (mem.begin (),mem.end ()),mem.end ()); sort (seg,seg+n*2 ); ll res=0 ; for (int i=0 ;i<n*2 ;i++) { if (i>0 ) res+=1ll *tr[1 ].len*(seg[i].x-seg[i-1 ].x); modify (1 ,find (seg[i].y1),find (seg[i].y2)-1 ,seg[i].k); } printf ("%lld" ,res); return 0 ; }
要求方差 ,我们需要维护的信息有 区间和 ,区间平方和 。
那么区间修改怎么下放标记呢?
通过简单的公式推导,我们可以得出:
那么这样下放标记就很简单了。
值得注意的是,要先更新区间平方和 ,因为这里用到了更新之前的区间和。
方差嘛就很好求了:
s 2 = ∑ i = l r a i 2 − a ‾ 2 s^2=\sum_{i=l}^{r}{a_i}^2-\overline{a}^2 s 2 = i = l ∑ r a i 2 − a 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 #include <bits/stdc++.h> using namespace std;const int N=1e5 +10 ;struct node { int l,r; double a,b,add; }tr[N<<2 ]; double a[N];int n,m;void pushup (int u) tr[u].a=tr[u<<1 ].a+tr[u<<1 |1 ].a; tr[u].b=tr[u<<1 ].b+tr[u<<1 |1 ].b; } void pushdown (int u) if (tr[u].add) { node &t=tr[u],&l=tr[u<<1 ],&r=tr[u<<1 |1 ]; l.b+=2 *t.add*l.a+(l.r-l.l+1 )*t.add*t.add; r.b+=2 *t.add*r.a+(r.r-r.l+1 )*t.add*t.add; r.a+=(r.r-r.l+1 )*t.add; l.a+=(l.r-l.l+1 )*t.add; r.add+=t.add; l.add+=t.add; t.add=0 ; } } void build (int u,int l,int r) tr[u].l=l,tr[u].r=r,tr[u].add=0 ; if (l==r) { tr[u].a=a[r]; tr[u].b=a[r]*a[r]; return ; } int mid=(l+r)>>1 ; build (u<<1 ,l,mid),build (u<<1 |1 ,mid+1 ,r); pushup (u); } void modify (int u,int l,int r,double x) if (tr[u].l>=l&&tr[u].r<=r) { tr[u].add+=x; tr[u].b+=(tr[u].r-tr[u].l+1 )*x*x+2 *x*tr[u].a; tr[u].a+=(tr[u].r-tr[u].l+1 )*x; return ; } pushdown (u); int mid=(tr[u].l+tr[u].r)>>1 ; if (l<=mid) modify (u<<1 ,l,r,x); if (r>mid) modify (u<<1 |1 ,l,r,x); pushup (u); } double query_0 (int u,int l,int r) if (tr[u].l>=l&&tr[u].r<=r) return tr[u].a; pushdown (u); int mid=(tr[u].l+tr[u].r)>>1 ; double ans=0 ; if (l<=mid) ans+=query_0 (u<<1 ,l,r); if (r>mid) ans+=query_0 (u<<1 |1 ,l,r); return ans; } double query_1 (int u,int l,int r) if (tr[u].l>=l&&tr[u].r<=r) return tr[u].b; pushdown (u); int mid=(tr[u].l+tr[u].r)>>1 ; double ans=0 ; if (l<=mid) ans+=query_1 (u<<1 ,l,r); if (r>mid) ans+=query_1 (u<<1 |1 ,l,r); return ans; } int main () scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=n;i++) scanf ("%lf" ,&a[i]); build (1 ,1 ,n); while (m--) { int op,l,r; scanf ("%d%d%d" ,&op,&l,&r); if (op==1 ) { double k; scanf ("%lf" ,&k); modify (1 ,l,r,k); } else if (op==2 ) printf ("%.4lf\n" ,query_0 (1 ,l,r)/(r-l+1 )); else if (op==3 ) printf ("%.4lf\n" ,query_1 (1 ,l,r)/(r-l+1 )-(query_0 (1 ,l,r)/(r-l+1 ))*(query_0 (1 ,l,r)/(r-l+1 ))); } return 0 ; }
经典的逆序对问题。
将数字看作树状数组的下标,由于数字的值域可能会很大,因此要先进行离散化。
假如是正序,每次把对应数字下标的元素加一,那么当前已经处理的数字的个数减去当前数字的下标的前缀和即为以该数字为较小数的逆序对的个数。
因为减去当前数字下标的前缀和即为减去所有小于这个数的个数,而已经在之前出现的小于等于该数的数显然不能与该数组成逆序对,所以该点对答案的贡献。
假如是倒序,那么就是当前数字前一个数字的前缀和即为对答案的贡献。这很显然,因为是倒序,所以出现过就相当于在当前元素的后面,也就是产生了逆序对,数字要减一是因为两个相同的数字组成不了逆序对。
正序代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 #include <bits/stdc++.h> #define lowbit(x) ((x)&(-x)) using namespace std;typedef long long ll;const int N=5e5 +10 ;int tr[N],rk[N],n;ll ans; struct point { int num,val; }a[N]; bool cmp (point x,point y) if (x.val==y.val) return x.num<y.num; return x.val<y.val; } void update (int x,int y) for (int i=x;i<=n;i+=lowbit (i)) tr[i]+=y; } ll query (int x) ll sum=0 ; for (int i=x;i;i-=lowbit (i)) sum+=tr[i]; return sum; } int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) { scanf ("%d" ,&a[i].val); a[i].num=i; } sort (a+1 ,a+1 +n,cmp); for (int i=1 ;i<=n;i++) rk[a[i].num]=i; for (int i=1 ;i<=n;i++) { update (rk[i],1 ); ans+=i-query (rk[i]); } printf ("%lld" ,ans); return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 #include <bits/stdc++.h> using namespace std;const int mod=998244353 ;const int N=5e5 +10 ;typedef long long ll;ll r[N],w[N],a[N]; int n,m,q;ll sum; ll tot; mt19937 rd (time(0 )) ;int main () scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=n;i++) w[i]=rd ()%mod,sum+=1ll *w[i],sum%=mod; while (m--) { int u,v; scanf ("%d%d" ,&u,&v); r[v]+=w[u]; a[v]=r[v]; tot+=w[u]; } scanf ("%d" ,&q); while (q--) { int op; scanf ("%d" ,&op); int u,v; if (op==1 ) { scanf ("%d%d" ,&u,&v); r[v]-=w[u]; tot-=w[u]; } else if (op==2 ) { scanf ("%d" ,&v); tot-=r[v]; r[v]=0 ; } else if (op==3 ) { scanf ("%d%d" ,&u,&v); r[v]+=w[u]; tot+=w[u]; } else if (op==4 ) { scanf ("%d" ,&v); tot+=a[v]-r[v]; r[v]=a[v]; } if (tot%mod==sum) printf ("YES\n" ); else printf ("NO\n" ); } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <bits/stdc++.h> using namespace std;int pmt[1000005 ];char a[1000005 ];int ans,n;int main () scanf ("%d" ,&n); scanf ("%s" ,a); for (int i=1 ,j=0 ;i<n;i++) { while (j&&a[i]!=a[j]) j=pmt[j-1 ]; if (a[i]==a[j]) j++; pmt[i]=j; } printf ("%d" ,n-pmt[n-1 ]); return 0 ; }
求一个 Border 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std;int n;int a[10000 ];int f[1000 ][1000 ];int sum[10000 ];int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&a[i]); for (int i=1 ;i<=n;i++) sum[i]=sum[i-1 ]+a[i]; memset (f,0x3f3f3f ,sizeof (f)); for (int i=1 ;i<=n;i++) f[i][i]=0 ; for (int len=2 ;len<=n;len++) for (int l=1 ,r=len;r<=n;r++,l++) for (int k=l;k<r;k++) f[l][r]=min (sum[r]-sum[l-1 ]+f[l][k]+f[k+1 ][r],f[l][r]); printf ("%d" ,f[1 ][n]); return 0 ; }
相较于链,复制出一份首尾相接即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <bits/stdc++.h> using namespace std;int n;int a[10000 ];int f[1000 ][1000 ];int sum[10000 ];int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&a[i]); for (int i=n+1 ;i<=2 *n;i++) a[i]=a[i-n]; for (int i=1 ;i<=2 *n;i++) sum[i]=sum[i-1 ]+a[i]; memset (f,0x3f ,sizeof (f)); for (int i=1 ;i<=2 *n;i++) f[i][i]=0 ; for (int len=2 ;len<=n;len++) for (int l=1 ,r=len;r<=2 *n;r++,l++) for (int k=l;k<r;k++) f[l][r]=min (sum[r]-sum[l-1 ]+f[l][k]+f[k+1 ][r],f[l][r]); int ans=f[1 ][n]; for (int l=1 ,r=n;r<=2 *n;l++,r++) ans=min (ans,f[l][r]); int maxn,minn; minn=ans; for (int len=2 ;len<=n;len++) for (int l=1 ,r=len;r<=2 *n;r++,l++) for (int k=l;k<r;k++) f[l][r]=max (sum[r]-sum[l-1 ]+f[l][k]+f[k+1 ][r],f[l][r]); ans=f[1 ][n]; for (int l=1 ,r=n;r<=2 *n;l++,r++) ans=max (ans,f[l][r]); maxn=ans; printf ("%d\n%d" ,minn,maxn); return 0 ; }
与上道题类似,注意转移的量和珠子贡献的产生。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> using namespace std;const int N=220 ;int n;int a[N];int f[N][N];int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&a[i]); for (int i=n+1 ;i<=2 *n;i++) a[i]=a[i-n]; for (int len=2 ;len<=n*2 ;len++) for (int l=1 ,r=len;r<=n*2 ;l++,r++) for (int k=l;k<r;k++) f[l][r]=max (f[l][r],f[l][k]+f[k+1 ][r]+a[l]*a[k+1 ]*a[r+1 ]); int ans=-1 ; for (int i=1 ;i<=n;i++) ans=max (ans,f[i][i+n-1 ]); printf ("%d" ,ans); return 0 ; }
注意初始位置不需要花时间,所以一开始不耗电,注意前缀和处理。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;const int N=100 ;int n,c;int a[N],v[N];int f[N][N][2 ];int main () scanf ("%d%d" ,&n,&c); for (int i=1 ;i<=n;i++) { scanf ("%d%d" ,&a[i],&v[i]); v[i]+=v[i-1 ]; } memset (f,0x3f ,sizeof (f)); f[c][c][0 ]=f[c][c][1 ]=0 ; for (int len=2 ;len<=n;len++) for (int l=1 ,r=len;r<=n;l++,r++) { f[l][r][0 ]=min (f[l+1 ][r][0 ]+(a[l+1 ]-a[l])*(v[l]+v[n]-v[r]),f[l+1 ][r][1 ]+(a[r]-a[l])*(v[l]+v[n]-v[r])); f[l][r][1 ]=min (f[l][r-1 ][1 ]+(a[r]-a[r-1 ])*(v[l-1 ]+v[n]-v[r-1 ]),f[l][r-1 ][0 ]+(a[r]-a[l])*(v[l-1 ]+v[n]-v[r-1 ])); } printf ("%d" ,min (f[1 ][n][0 ],f[1 ][n][1 ])); return 0 ; }
l ∼ r l\sim{r} l ∼ r l + 1 ∼ r l+1\sim{r} l + 1 ∼ r l ∼ r − 1 l\sim{r-1} l ∼ r − 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 #include <bits/stdc++.h> using namespace std;const int N=2005 ;int a[N],f[N][N];int n;int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&a[i]); for (int i=1 ;i<=n;i++) f[i][i]=a[i]*n; for (int len=2 ;len<=n;len++) for (int l=1 ,r=len;r<=n;l++,r++) f[l][r]=max (f[l][r-1 ]+a[r]*(n-len+1 ),f[l+1 ][r]+a[l]*(n-len+1 )); printf ("%d" ,f[1 ][n]); return 0 ; }
原来最大为 40 40 4 0 l o g n logn l o g n 58 58 5 8
注意处理为左闭右开区间方便合并,不然左右端点共用没法处理。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> using namespace std;const int N=3e5 +7 ;int a,n,ans;int f[60 ][N];int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&a),f[a][i]=i+1 ; for (int i=2 ;i<=58 ;i++) for (int j=1 ;j<=n;j++) { if (!f[i][j]) f[i][j]=f[i-1 ][f[i-1 ][j]]; if (f[i][j]) ans=i; } printf ("%d" ,ans); return 0 ; }
同上,注意请使用左闭右开区间,为此还发了篇讨论区。
通过以上两题,我们可以总结出两条规律:
合并区间时请使用左闭右开区间。 设计状态时,以值域较小的变量作为数组下标,就像本题并没有选择传统的 l , r l,r l , r 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> using namespace std;const int N=3e5 +7 ;int a,n,ans;int f[60 ][N];int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&a),f[a][i]=i+1 ; for (int i=2 ;i<=58 ;i++) for (int j=1 ;j<=n;j++) { if (!f[i][j]) f[i][j]=f[i-1 ][f[i-1 ][j]]; if (f[i][j]) ans=i; } printf ("%d" ,ans); return 0 ; }
见注释。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 #include <bits/stdc++.h> using namespace std;const int mod=19650827 ;const int N=1005 ;int n,a[N];int f[N][N][2 ];int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&a[i]),f[i][i][0 ]=1 ; for (int len=2 ;len<=n;len++) for (int l=1 ,r=len;r<=n;l++,r++) { if (a[l]<a[l+1 ]) f[l][r][0 ]=(f[l][r][0 ]+f[l+1 ][r][0 ])%mod; if (a[l]<a[r]) f[l][r][0 ]=(f[l][r][0 ]+f[l+1 ][r][1 ])%mod; if (a[r]>a[l]) f[l][r][1 ]=(f[l][r][1 ]+f[l][r-1 ][0 ])%mod; if (a[r]>a[r-1 ]) f[l][r][1 ]=(f[l][r][1 ]+f[l][r-1 ][1 ])%mod; } printf ("%d" ,(f[1 ][n][0 ]+f[1 ][n][1 ])%mod); return 0 ; }
首先初始化一个区间只需要涂一次。
枚举区间,假如区间左右端点的颜色相同,那么就可以在之前一起涂上,所以就可以从 l + 1 ∼ r l+1\sim{r} l + 1 ∼ r l ∼ r − 1 l\sim{r-1} l ∼ r − 1
假如不同的话,那就需要枚举分界点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;const int N=60 ;int f[N][N];string s; int main () cin>>s; int n=s.length (); memset (f,0x3f ,sizeof (f)); for (int i=0 ;i<n;i++) f[i][i]=1 ; for (int len=2 ;len<=n;len++) for (int l=0 ,r=len-1 ;r<n;l++,r++) { if (s[l]==s[r]) { f[l][r]=min (f[l][r],min (f[l+1 ][r],f[l][r-1 ])); continue ; } for (int k=l;k<r;k++) f[l][r]=min (f[l][r],f[l][k]+f[k+1 ][r]); } printf ("%d" ,f[0 ][n-1 ]); return 0 ; }
状态定义为区间 l ∼ r l\sim{r} l ∼ r k k k k k k
p p p f 1 , f 2 f_1,f_2 f 1 , f 2 f 1 f_1 f 1 f 2 f_2 f 2 p p p
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 #include <bits/stdc++.h> using namespace std;const int N=205 ;bool f[N][N][5 ];char a[10 ];vector<string> s[5 ]; int w,o,n,g;int ch (char c) if (c=='W' ) return 1 ; if (c=='I' ) return 2 ; if (c=='N' ) return 3 ; if (c=='G' ) return 4 ; return 0 ; } string name; int main () scanf ("%d%d%d%d" ,&w,&o,&n,&g); for (int i=1 ;i<=w;i++) { scanf ("%s" ,a); s[1 ].emplace_back (a); } for (int i=1 ;i<=o;i++) { scanf ("%s" ,a); s[2 ].emplace_back (a); } for (int i=1 ;i<=n;i++) { scanf ("%s" ,a); s[3 ].emplace_back (a); } for (int i=1 ;i<=g;i++) { scanf ("%s" ,a); s[4 ].emplace_back (a); } cin>>name; int length=name.length (); for (int i=0 ;i<length;i++) f[i][i][ch (name[i])]=true ; for (int i=2 ;i<=length;i++) for (int l=0 ,r=i-1 ;r<length;l++,r++) for (int k=l;k<r;k++) for (int p=1 ;p<=4 ;p++) for (auto &v:s[p]) { char f1=v[0 ],f2=v[1 ]; if (f[l][k][ch (f1)]&&f[k+1 ][r][ch (f2)]) f[l][r][p]=true ; } bool bj=false ; if (f[0 ][length-1 ][1 ]) bj=true ,printf ("W" ); if (f[0 ][length-1 ][2 ]) bj=true ,printf ("I" ); if (f[0 ][length-1 ][3 ]) bj=true ,printf ("N" ); if (f[0 ][length-1 ][4 ]) bj=true ,printf ("G" ); if (!bj) printf ("The name is wrong!" ); return 0 ; }
首先断环为链,考虑转移。
如果是加法,那直接取max肯定没问题,但是有乘法,并且有负数,就要考虑负负得正的情况,而且最大值乘以一个负数后便不再是最大值,所以我们还要维护一个区间答案最小值。
转移的时候,左右两半部分都有可能是正或者负,所以四种情况取一个最大值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <bits/stdc++.h> using namespace std;typedef long long ll;const int N=160 ;int n;ll ans; char cl[N];int a[N];ll f[N][N],g[N][N]; int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf (" %c %d" ,&cl[i],&a[i]); for (int i=n+1 ;i<=2 *n;i++) cl[i]=cl[i-n],a[i]=a[i-n]; memset (f,-127 ,sizeof (f)); memset (g,127 ,sizeof (f)); for (int i=1 ;i<=n*2 ;i++) f[i][i]=g[i][i]=a[i]; for (int len=2 ;len<=n;len++) for (int l=1 ,r=len;r<=n*2 ;l++,r++) for (int k=l;k<r;k++) { if (cl[k+1 ]=='t' ) { f[l][r]=max (f[l][r],f[l][k]+f[k+1 ][r]); g[l][r]=min (g[l][r],g[l][k]+g[k+1 ][r]); } if (cl[k+1 ]=='x' ) { f[l][r]=max (f[l][r],max (f[l][k]*f[k+1 ][r],max (g[l][k]*g[k+1 ][r],max (f[l][k]*g[k+1 ][r],g[l][k]*f[k+1 ][r])))); g[l][r]=min (g[l][r],min (f[l][k]*f[k+1 ][r],min (g[l][k]*g[k+1 ][r],min (f[l][k]*g[k+1 ][r],g[l][k]*f[k+1 ][r])))); } } for (int i=1 ;i<=n+1 ;i++) ans=max (ans,f[i][i+n-1 ]); printf ("%lld\n" ,ans); for (int i=1 ;i<=n;i++) if (f[i][i+n-1 ]==ans) printf ("%d " ,i); return 0 ; }
分裂太复杂不太好想,不如反过来考虑,如何把给定的字符串合成为长度尽量小的 S,f i , j f_{i,j} f i , j [ i , j ] [i,j] [ i , j ] h i , j h_{i,j} h i , j [ i , j ] [i,j] [ i , j ]
之所以要状态压缩而不是直接赋值编号的原因是某个区间会被多个字符有可能取代,而它们只需要满足一个就可以转移。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 #include <bits/stdc++.h> using namespace std;const int N=120 ;int n,m;char a[N];int f[N][N];int mp[N][N];int h[N][N];int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) { scanf ("%s" ,a); mp[a[1 ]-'A' +1 ][a[2 ]-'A' +1 ]|=(1 <<(a[0 ]-'A' +1 )); } scanf ("%d" ,&m); for (int i=1 ;i<=m;i++) { memset (f,0x3f ,sizeof (f)); memset (h,0 ,sizeof (h)); scanf ("%s" ,a); int len=strlen (a); for (int j=0 ;j<len;j++) { if (a[j]=='S' ) f[j+1 ][j+1 ]=1 ; h[j+1 ][j+1 ]|=(1 <<(a[j]-'A' +1 )); } for (int j=1 ;j<=len;j++) for (int l=1 ,r=j;r<=len;l++,r++) { for (int k=l;k<r;k++) { f[l][r]=min (f[l][r],f[l][k]+f[k+1 ][r]); for (int x=1 ;x<=26 ;x++) for (int y=1 ;y<=26 ;y++) if ((h[l][k]&(1 <<x))&&(h[k+1 ][r]&(1 <<y))) h[l][r]|=mp[x][y]; } if (h[l][r]&(1 <<('S' -'A' +1 ))) f[l][r]=1 ; } if (f[1 ][len]>=0x3f3f3f3f ) printf ("NIE\n" ); else printf ("%d\n" ,f[1 ][len]); } return 0 ; }
这道题相当于是关路灯的升级版。需要先按照横坐标排个序,并且没有固定的起点。
我们可以利用关路灯的思路,求最小下降的总高度,用一开始的总高度减去就可以了。
而本题中一开始不一定在某个彩蛋下面,关路灯是从某个确定的路灯下开始的,所以我们要预处理出它一开始到每个彩蛋的花费(其实预处理出最小的就可以了,但是为了方便不如一起预处理了)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;typedef long long ll;const int N=1005 ;ll f[N][N][2 ]; int x_0,n;struct egg { int x,y,v; bool operator <(const egg &a)const { return x<a.x; } }eg[N]; int sum[N];double ans;int main () scanf ("%d%d" ,&n,&x_0); for (int i=1 ;i<=n;i++) scanf ("%d" ,&eg[i].x); for (int i=1 ;i<=n;i++) scanf ("%d" ,&eg[i].y),ans+=1.0 *eg[i].y; for (int i=1 ;i<=n;i++) scanf ("%d" ,&eg[i].v); sort (eg+1 ,eg+1 +n); for (int i=1 ;i<=n;i++) sum[i]=sum[i-1 ]+eg[i].v; memset (f,0x3f ,sizeof (f)); for (int i=1 ;i<=n;i++) f[i][i][0 ]=f[i][i][1 ]=1ll *sum[n]*abs (x_0-eg[i].x); for (int i=2 ;i<=n;i++) for (int l=1 ,r=i;r<=n;l++,r++) { f[l][r][0 ]=min (f[l+1 ][r][0 ]+1ll *(sum[l]+sum[n]-sum[r])*(eg[l+1 ].x-eg[l].x),f[l+1 ][r][1 ]+1ll *(sum[l]+sum[n]-sum[r])*(eg[r].x-eg[l].x)); f[l][r][1 ]=min (f[l][r-1 ][1 ]+1ll *(sum[l-1 ]+sum[n]-sum[r-1 ])*(eg[r].x-eg[r-1 ].x),f[l][r-1 ][0 ]+1ll *(sum[l-1 ]+sum[n]-sum[r-1 ])*(eg[r].x-eg[l].x)); } ans-=(double )min (f[1 ][n][0 ],f[1 ][n][1 ]); ans/=1000.0 ; printf ("%.3lf" ,ans); return 0 ; }
对每个右端点记录它对应的左端点,从小到大枚举右端点,区间扩大了那么肯定至少能继承之前的区间,假如它对应的某个左端点之前也有贡献,那么就可以新加入这个区间的贡献。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;const int N=3e6 +10 ;vector<int > a[N]; int n,maxn;int f[N];int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) { int x,y; scanf ("%d%d" ,&x,&y); a[y].emplace_back (x); maxn=max (maxn,y); } for (int i=1 ;i<=maxn;i++) { f[i]=max (f[i],f[i-1 ]); for (auto &j:a[i]) f[i]=max (f[i],f[j-1 ]+i-j+1 ); } printf ("%d" ,f[maxn]); return 0 ; }
倒叙枚举,考虑后缀,如果当前有任务,那就拿当前所能获得的最大空闲时间与完成任务后得到的最大空闲时间取一个 max,如果当前空闲,那就可以多一分钟的空闲时间。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;const int N=1e4 +10 ;int n,k;vector<int > a[N]; int f[N];int main () scanf ("%d%d" ,&n,&k); for (int i=1 ;i<=k;i++) { int x,y; scanf ("%d%d" ,&x,&y); a[x].emplace_back (y); } for (int i=n;i>=1 ;i--) { if (a[i].size ()) for (auto &j:a[i]) f[i]=max (f[i],f[i+j]); else f[i]=f[i+1 ]+1 ; } printf ("%d" ,f[1 ]); return 0 ; }
求单调不降子序列的个数其实就是求最长上升子序列的长度,注意要对 l l l
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> #define lowbit(x) ((x)&(-x)) using namespace std;const int N=1e5 ;int n,ans=-1 ,maxn=-1 ;int f[N];void update (int u,int v) for (int i=u;i<=maxn;i+=lowbit (i)) f[i]=max (f[i],v); } int query (int x) int res=0 ; for (int i=x;i;i-=lowbit (i)) res=max (res,f[i]); return res; } struct edge { int l,w; bool operator <(const edge &x)const { if (l!=x.l) return l>x.l; return w>x.w; } }e[N]; int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d %d" ,&e[i].l,&e[i].w),maxn=max (maxn,e[i].w); sort (e+1 ,e+1 +n); for (int i=1 ;i<=n;i++) { int q=query (e[i].w-1 ); update (e[i].w,q+1 ); ans=max (ans,q+1 ); } printf ("%d" ,ans); return 0 ; }
其实就是求拐点的数量,注意不能算开头。
绝妙的异或代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <bits/stdc++.h> using namespace std;const int N=1e3 +10 ;int n,p,q,bj,ans=1 ;int a[N];int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) { p=q; scanf ("%d" ,&q); if (p==q) continue ; if (bj^(q<p)) { ans++,bj=q<p; } } printf ("%d" ,ans); return 0 ; }
与木棍加工类似。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <bits/stdc++.h> #define lowbit(x) ((x)&(-x)) using namespace std;const int N=1e6 +10 ;int n,ans=-1 ,maxn=-1 ;int f[N];void update (int u,int v) for (int i=u;i<=maxn;i+=lowbit (i)) f[i]=max (f[i],v); } int query (int x) int res=0 ; for (int i=x;i;i-=lowbit (i)) res=max (res,f[i]); return res; } struct edge { int l,w; bool operator <(const edge &x)const { return l<x.l; } }e[N]; int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d %d" ,&e[i].l,&e[i].w),maxn=max (maxn,e[i].w); sort (e+1 ,e+1 +n); for (int i=1 ;i<=n;i++) { int q=query (e[i].w-1 ); update (e[i].w,q+1 ); ans=max (ans,q+1 ); } printf ("%d" ,ans); return 0 ; }
我们分别计算闪烁和跑步的距离,能闪烁是一定闪烁的,假如某时刻闪烁更优,只需要把跑步替换成闪烁即可,否则就只进行跑步,如果到了终点直接就退出。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <bits/stdc++.h> using namespace std;const int N=3e5 +7 ;int s1,s2;int m,s,t;int main () scanf ("%d%d%d" ,&m,&s,&t); for (int i=1 ;i<=t;i++) { s1+=17 ; if (m>=10 ) { s2+=60 ; m-=10 ; } else m+=4 ; if (s2>s1) s1=s2; if (s1>=s) { printf ("Yes\n%d\n" ,i); return 0 ; } } printf ("No\n%d\n" ,s1); return 0 ; }
状态定义见注释,转移分情况讨论,注意滚动数组优化空间。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> using namespace std;const int mod=1000000007 ;const int N=1010 ;int n,m,k;char a[N],b[220 ];int f[2 ][220 ][220 ][2 ];bool bj;int main () scanf ("%d%d%d" ,&n,&m,&k); scanf ("%s\n%s" ,a,b); f[0 ][0 ][0 ][0 ]=f[1 ][0 ][0 ][0 ]=1 ; bj=true ; for (int i=1 ;i<=n;i++,bj=!bj) for (int j=1 ;j<=m;j++) for (int l=1 ;l<=k;l++) { if (a[i-1 ]==b[j-1 ]) { f[bj][j][l][0 ]=(f[!bj][j][l][0 ]+f[!bj][j][l][1 ])%mod; f[bj][j][l][1 ]=(f[!bj][j-1 ][l-1 ][0 ]+(f[!bj][j-1 ][l-1 ][1 ]+f[!bj][j-1 ][l][1 ])%mod)%mod; } else { f[bj][j][l][0 ]=(f[!bj][j][l][0 ]+f[!bj][j][l][1 ])%mod; f[bj][j][l][1 ]=0 ; } } printf ("%d" ,(f[!bj][m][k][0 ]+f[!bj][m][k][1 ])%mod); return 0 ; }
定义 f i , j , k f_{i,j,k} f i , j , k i i i j j j k k k
首先中国象棋要使得每个炮互不攻击,每行每列的炮的数量不能超过两个,所以数量有三种状态,由于知道两个剩下一个就可以算出来,所以只需要记录两个。
考虑在下一行放零个炮还是一个炮还是两个炮,分别写出转移式子。
假如下一行不放炮,那么就直接继承。
假如下一行放一个炮,这个炮可能放在一个炮的列,也可能放在零个炮的列。
假如下一行放两个炮,那么有可能这两个炮都放在零个炮的列,有可能都放在一个炮的列,也有可能一个炮放在零个炮的列,一个放在一个炮的列,这里就需要预处理一下 2 的组合数了。
最后统计答案的时候,每种情况取一个 max。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;const int mod=9999973 ;int n,m;int ans;int f[105 ][105 ][105 ];int c[105 ][105 ];void init () for (int i=2 ;i<=105 ;i++) c[i][2 ]=i*(i-1 )/2 %mod; } int main () scanf ("%d%d" ,&n,&m); init (); f[0 ][m][0 ]=1 ; for (int i=0 ;i<=n-1 ;i++) for (int j=0 ;j<=m;j++) for (int k=0 ;k<=m-j;k++) { f[i+1 ][j][k]=(f[i+1 ][j][k]+f[i][j][k])%mod; if (j>=1 ) f[i+1 ][j-1 ][k+1 ]=(f[i+1 ][j-1 ][k+1 ]+(1ll *f[i][j][k]*j%mod))%mod; if (k>=1 ) f[i+1 ][j][k-1 ]=(f[i+1 ][j][k-1 ]+(1ll *f[i][j][k]*k%mod))%mod; if (j>=1 ) f[i+1 ][j-1 ][k]=(f[i+1 ][j-1 ][k]+(1ll *f[i][j][k]*j*k%mod))%mod; if (j>=2 ) f[i+1 ][j-2 ][k+2 ]=(f[i+1 ][j-2 ][k+2 ]+(1ll *f[i][j][k]*c[j][2 ]%mod))%mod; if (k>=2 ) f[i+1 ][j][k-2 ]=(f[i+1 ][j][k-2 ]+(1ll *f[i][j][k]*c[k][2 ]%mod))%mod; } for (int i=0 ;i<=m;i++) for (int j=0 ;j<=m-i;j++) ans=(ans+f[n][i][j])%mod; printf ("%d" ,ans); return 0 ; }
由于本题不仅可以向下,还可以向上,所以不能像数字三角形那样进行转移。
因为不能走重复的路,所以我们可以再开一维,记录它是从上方转移而来还是从下方转移而来,因为假如它这步走了向下,那么它上一步如果也是纵向移动的话也一定是向下。
从左向右的转移还是正常进行,这时候不考虑上一步是从上方走来还是从下方走来。
对于向下走,正序枚举一遍,对于向上走,倒叙枚举一遍即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> using namespace std;const int N=1e3 +10 ;typedef long long ll;int n,m;int number[N][N];ll f[N][N][2 ]; int main () scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=n;i++) for (int j=1 ;j<=m;j++) scanf ("%d" ,&number[i][j]); memset (f,0xc0 ,sizeof (f)); f[1 ][1 ][0 ]=f[1 ][1 ][1 ]=number[1 ][1 ]; for (int j=1 ;j<=m;j++) { for (int i=1 ;i<=n;i++) { if (j-1 >=1 ) { f[i][j][0 ]=max (f[i][j][0 ],max (f[i][j-1 ][0 ],f[i][j-1 ][1 ])+number[i][j]); f[i][j][1 ]=max (f[i][j][1 ],max (f[i][j-1 ][0 ],f[i][j-1 ][1 ])+number[i][j]); } if (i-1 >=1 ) f[i][j][1 ]=max (f[i][j][1 ],f[i-1 ][j][1 ]+number[i][j]); } for (int i=n-1 ;i>=1 ;i--) f[i][j][0 ]=max (f[i][j][0 ],f[i+1 ][j][0 ]+number[i][j]); } printf ("%lld" ,max (f[n][m][1 ],f[n][m][0 ])); return 0 ; }
注释已述备矣。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <bits/stdc++.h> using namespace std;int n, m, t, ans;char a[55 ][55 ];int f[55 ][2505 ];int g[55 ][2505 ][55 ];int sum[55 ][2505 ];int main () scanf ("%d%d%d" , &n, &m, &t); for (int i = 1 ; i <= n; i++) { scanf ("%s" , a[i]); for (int j = 0 ; j < m; j++) { if (a[i][j] == '1' ) sum[i][j + 1 ] = sum[i][j] + 1 ; else sum[i][j + 1 ] = sum[i][j]; } } for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= m; j++) for (int k = 1 ; k <= m; k++) for (int q = j - 1 ; q < k; q++) g[i][j][k] = max (g[i][j][k], g[i][j - 1 ][q] + max (sum[i][k] - sum[i][q], k - q - sum[i][k] + sum[i][q])); for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= t; j++) for (int k = 0 ; k <= min (j, m); k++) f[i][j] = max (f[i][j], f[i - 1 ][j - k] + g[i][k][m]); for (int i = 1 ; i <= t; i++) ans = max (ans, f[n][i]); cout << ans << endl; return 0 ; }
还不是很懂第一篇题解的做法,到时候懂了来补。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;const int N = 1e6 + 7 ;const int INF = 0x3f3f3f3f ;int f[3 ]; int a[N];int main () int n; scanf ("%d" , &n); for (int i = 1 ; i <= n; i++) scanf ("%d" , &a[i]); f[0 ] = f[1 ] = f[2 ] = INF; f[a[1 ] + 1 ] = 0 ; for (int i = 2 ; i <= n; i++) { if (a[i] == -1 ) { f[1 ] = INF; f[2 ] += 2 ; } else if (a[i] == 0 ) { f[1 ] = min (f[0 ], f[1 ]); f[0 ]++; f[2 ]++; } else { f[2 ] = min (f[0 ], min (f[1 ], f[2 ])); f[1 ] = f[0 ] + 1 ; f[0 ] += 2 ; } } int ans = min (f[0 ], min (f[1 ], f[2 ])); if (ans < INF) cout << ans << endl; else cout << "BRAK" << endl; return 0 ; }
经典 0 / 1 背包问题,不过有两种限制,都加入状态即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <bits/stdc++.h> using namespace std;int n, m, t;int mm[101 ], tt[101 ];int f[201 ][201 ];int main () scanf ("%d%d%d" , &n, &m, &t); for (int i = 1 ; i <= n; i++) scanf ("%d%d" , &mm[i], &tt[i]); for (int i = 1 ; i <= n; i++) for (int j = m; j >= mm[i]; j--) for (int k = t; k >= tt[i]; k--) f[j][k] = max (f[j][k], f[j - mm[i]][k - tt[i]] + 1 ); cout << f[m][t] << endl; return 0 ; }
A 集合中可以被除了自己的金币表示的面额一定没用,剩下的就是最小的 m。
设 f i f_i f i i i i a a a
假如 x x x a a a x x x a i a_i a i
减去之后,x − a i x - a_i x − a i a a a
枚举一下比当前面额大的然后用当前面额更新它们即可。
初始化 f 0 = 1 f_0=1 f 0 = 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;bool f[25555 ]; int main () int t; scanf ("%d" , &t); while (t--) { memset (f, 0 , sizeof (f)); int n; int a[110 ]; scanf ("%d" , &n); int ans = n; for (int i = 1 ; i <= n; i++) scanf ("%d" , &a[i]); sort (a + 1 , a + 1 + n); f[0 ] = 1 ; for (int i = 1 ; i <= n; i++) { if (f[a[i]]) { ans--; continue ; } for (int j = a[i]; j <= a[n]; j++) f[j] |= f[j - a[i]]; } cout << ans << endl; } return 0 ; }
由于最多只有两个附件,所以我们正常枚举主件,然后看看附件选不选怎么选优即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <bits/stdc++.h> using namespace std;const int N = 32010 ;int v[N], w[N], p[N];int f[N];int mp[66 ][3 ];vector<int > mm; int main () int n, m; scanf ("%d%d" , &n, &m); for (int i = 1 ; i <= m; i++) { scanf ("%d%d%d" , &w[i], &v[i], &p[i]); if (p[i]) { if (!mp[p[i]][1 ]) mp[p[i]][1 ] = i; else mp[p[i]][2 ] = i; } else mm.push_back (i); } for (auto &i : mm) for (int j = n; j >= w[i]; j--) { int val0 = w[i] * v[i], val1 = w[mp[i][1 ]] * v[mp[i][1 ]], val2 = w[mp[i][2 ]] * v[mp[i][2 ]]; f[j] = max (f[j], f[j - w[i]] + val0); if (j >= w[i] + w[mp[i][1 ]] && val1) f[j] = max (f[j], f[j - w[i] - w[mp[i][1 ]]] + val0 + val1); if (j >= w[i] + w[mp[i][2 ]] && val2) f[j] = max (f[j], f[j - w[i] - w[mp[i][2 ]]] + val0 + val2); if (j >= w[i] + w[mp[i][1 ]] + w[mp[i][2 ]] && val1 && val2) f[j] = max (f[j], f[j - w[i] - w[mp[i][1 ]] - w[mp[i][2 ]]] + val0 + val1 + val2); } cout << f[n] << endl; return 0 ; }
考虑模数为状态,然后正常考虑每一个牛选不选的方案数,最后输出模数为 0 的状态即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 #include <bits/stdc++.h> using namespace std;const int MOD = 1e8 ;const int N = 2005 ;const int M = 1001 ;int f[M]; int a[N];int main () int n, c; scanf ("%d%d" , &n, &c); for (int i = 1 ; i <= n; i++) { scanf ("%d" , &a[i]); } for (int i = 1 ; i <= n; i++) f[a[i] % c] = 1 ; for (int i = 1 ; i <= n; i++) { for (int j = c - 1 ; j >= 0 ; j--) { f[j] = (f[j] + f[j] % MOD + f[(j - a[i] % c + c) % c] % MOD) % MOD; } } cout << f[0 ] << endl; return 0 ; }
用 f i f_i f i i i i
枚举当前要决定堆哪个,用旧状态更新新状态,然后把旧状态更新为可以吃垃圾的新状态。
这里的顺序非常精妙,值得深思。
短短的代码,大大的智慧。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;const int N = 101 ;const int M = 1050 ;struct De { int t, p, h; bool operator < (const De &a) const { return t < a.t; } }de[N]; int f[N]; int main () int d, g; scanf ("%d%d" , &d, &g); for (int i = 1 ; i <= g; i++) scanf ("%d%d%d" , &de[i].t, &de[i].p, &de[i].h); sort (de + 1 , de + 1 + g); f[0 ] = 10 ; for (int i = 1 ; i <= g; i++) for (int j = d; j >= 0 ; j--) { if (f[j] >= de[i].t) { if (j + de[i].h >= d) { cout << de[i].t << endl; return 0 ; } f[j + de[i].h] = max (f[j + de[i].h], f[j]); f[j] += de[i].p; } } cout << f[0 ] << endl; return 0 ; }
树形背包问题。
倒叙枚举体积把枚举到第几个儿子这个状态给滚掉,详情见DP-背包问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <bits/stdc++.h> using namespace std;const int N=305 ;int n,m,edcnt;int f[N][N];int s[N];int fir[N];struct edge { int to,nxt; }e[N]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void dfs (int u) for (int i=fir[u];i;i=e[i].nxt) { int v=e[i].to; dfs (v); for (int j=m+1 ;j>=1 ;j--) for (int k=0 ;k<j;k++) f[u][j]=max (f[u][j],f[v][k]+f[u][j-k]); } } int main () scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=n;i++) { int k; scanf ("%d%d" ,&k,&s[i]); f[i][1 ]=s[i]; add (k,i); } dfs (0 ); printf ("%d" ,f[0 ][m+1 ]); return 0 ; }
本质为树的最大独立集问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <bits/stdc++.h> using namespace std;const int N=6e3 +7 ;int n,edcnt;int r[N];int f[N][2 ];int fir[N];struct edge { int nxt,to; }e[N<<1 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void dfs (int u,int fa) for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; dfs (v,u); } f[u][1 ]=r[u]; for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; f[u][0 ]+=max (f[v][0 ],f[v][1 ]); f[u][1 ]+=f[v][0 ]; } } int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&r[i]); for (int i=1 ;i<=n-1 ;i++) { int l,k; scanf ("%d%d" ,&l,&k); add (k,l); add (l,k); } dfs (1 ,-1 ); printf ("%d" ,max (f[1 ][0 ],f[1 ][1 ])); return 0 ; }
与没有上司的舞会类似。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> using namespace std;const int N=2000 ;int fir[N];int f[N][2 ];int n,edcnt;struct edge { int to,nxt; }e[N<<1 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void dfs (int u,int fa) f[u][1 ]=1 ,f[u][0 ]=0 ; for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; dfs (v,u); f[u][1 ]+=min (f[v][0 ],f[v][1 ]); f[u][0 ]+=f[v][1 ]; } } int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) { int u,k,v; scanf ("%d%d" ,&u,&k); u++; for (int j=1 ;j<=k;j++) { scanf ("%d" ,&v); add (u,++v); add (v,u); } } dfs (1 ,-1 ); printf ("%d" ,min (f[1 ][0 ],f[1 ][1 ])); return 0 ; }
典型的树形背包问题,问题在于合并两颗子树,状态定义见注释。
对于一个子树,它的根节点有四种可能的情况:没放置没被监听,没放置被监听,放置没被监听,放置被监听。
然后对这些另一个子树的情况进行分类讨论即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #include <bits/stdc++.h> using namespace std;const int N=1e5 +7 ;const int mod=1e9 +7 ;int n,k;int edcnt;int fir[N],siz[N];int f[N][2 ][2 ][101 ];int temp[2 ][2 ][101 ];struct edge { int nxt,to; }e[N<<1 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void dp (int u,int fa) siz[u]=1 ; f[u][1 ][0 ][1 ]=1 ; f[u][0 ][0 ][0 ]=1 ; for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; dp (v,u); for (int j=0 ;j<=min (siz[u],k);j++) { temp[0 ][0 ][j]=f[u][0 ][0 ][j]; f[u][0 ][0 ][j]=0 ; temp[1 ][0 ][j]=f[u][1 ][0 ][j]; f[u][1 ][0 ][j]=0 ; temp[0 ][1 ][j]=f[u][0 ][1 ][j]; f[u][0 ][1 ][j]=0 ; temp[1 ][1 ][j]=f[u][1 ][1 ][j]; f[u][1 ][1 ][j]=0 ; } for (int j=0 ;j<=min (siz[u],k);j++) for (int l=0 ;l<=min (siz[v],k-j);l++) { f[u][0 ][0 ][j+l]=(1ll *f[u][0 ][0 ][j+l]+1ll *temp[0 ][0 ][j]*f[v][0 ][1 ][l])%mod; f[u][0 ][1 ][j+l]=(1ll *f[u][0 ][1 ][j+l]+1ll *temp[0 ][1 ][j]*(f[v][0 ][1 ][l]+f[v][1 ][1 ][l])%mod+1ll *temp[0 ][0 ][j]*f[v][1 ][1 ][l])%mod; f[u][1 ][0 ][j+l]=(1ll *f[u][1 ][0 ][j+l]+1ll *temp[1 ][0 ][j]*(f[v][0 ][0 ][l]+f[v][0 ][1 ][l]))%mod; f[u][1 ][1 ][j+l]=((1ll *f[u][1 ][1 ][j+l]+1ll *temp[1 ][0 ][j]*(f[v][1 ][0 ][l]+f[v][1 ][1 ][l]))%mod+1ll *temp[1 ][1 ][j]*(1ll *f[v][0 ][0 ][l]+1ll *f[v][0 ][1 ][l]+1ll *f[v][1 ][0 ][l]+1ll *f[v][1 ][1 ][l]))%mod; } siz[u]+=siz[v]; } } int main () scanf ("%d%d" ,&n,&k); for (int i=1 ;i<n;i++) { int u,v; scanf ("%d%d" ,&u,&v); add (u,v); add (v,u); } dp (1 ,-1 ); printf ("%d" ,(f[1 ][0 ][1 ][k]+f[1 ][1 ][1 ][k])%mod); return 0 ; }
常规树形DP。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> using namespace std;const int N=2e4 +7 ;int n,edcnt;int beauty[N];int fir[N];int f[N];struct edge { int nxt,to; }e[N<<1 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void dp (int u,int fa) f[u]=beauty[u]; for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; dp (v,u); f[u]+=max (f[v],0 ); } } int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) scanf ("%d" ,&beauty[i]); for (int i=1 ;i<n;i++) { int u,v; scanf ("%d%d" ,&u,&v); add (u,v); add (v,u); } dp (1 ,-1 ); int ans=-0x3f3f3f3f ; for (int i=1 ;i<=n;i++) ans=max (ans,f[i]); printf ("%d" ,ans); return 0 ; }
对于叶子节点,它满足一个用户的最大收益就是对应价值,然后转移时当作背包来做,用户总数量相当于背包容量,最后我们就是找找看以1为根的子树中最大收益大于等于零的最大用户数,倒叙枚举即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 #include <bits/stdc++.h> using namespace std;const int N=3100 ;int n,m,edcnt;int pay[N];int fir[N];int f[N][N];struct edge { int to,nxt,val; }e[N<<1 ]; void add (int u,int v,int w) e[++edcnt].to=v; e[edcnt].val=w; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } int dp (int u) if (!fir[u]) { f[u][1 ]=pay[u]; return 1 ; } int sum=0 ; for (int i=fir[u];i;i=e[i].nxt) { int v=e[i].to; int x=dp (v); sum+=x; for (int j=sum;j>=1 ;j--) for (int k=1 ;k<=x;k++) if (j-k>=0 ) f[u][j]=max (f[u][j],f[u][j-k]+f[v][k]-e[i].val); } return sum; } int main () scanf ("%d%d" ,&n,&m); for (int i=1 ;i<=n-m;i++) { int k; scanf ("%d" ,&k); for (int j=1 ;j<=k;j++) { int a,c; scanf ("%d%d" ,&a,&c); add (i,a,c); } } for (int i=1 ;i<=m;i++) scanf ("%d" ,&pay[n-m+i]); memset (f,0xc0 ,sizeof (f)); for (int i=1 ;i<=n;i++) f[i][0 ]=0 ; dp (1 ); for (int i=m;i>=0 ;i--) if (f[1 ][i]>=0 ) { printf ("%d" ,i); return 0 ; } return 0 ; }
状态设计为 f i , j f_{i,j} f i , j i i i j j j
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 #include <bits/stdc++.h> using namespace std;const int N=1e5 +7 ;int n,k,edcnt;int val[N];int fir[N];int f[N][27 ];struct edge { int nxt,to; }e[N<<1 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void dp (int u,int fa) for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; dp (v,u); for (int j=1 ;j<=k;j++) f[u][j]+=f[v][j-1 ]; } } void dfs (int u,int fa) for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; for (int j=k;j>=2 ;j--) f[v][j]-=f[v][j-2 ]; for (int j=1 ;j<=k;j++) f[v][j]+=f[u][j-1 ]; dfs (v,u); } } int main () scanf ("%d%d" ,&n,&k); for (int i=1 ;i<=n-1 ;i++) { int u,v; scanf ("%d%d" ,&u,&v); add (u,v); add (v,u); } for (int i=1 ;i<=n;i++) scanf ("%d" ,&val[i]),f[i][0 ]=val[i]; dp (1 ,-1 ); dfs (1 ,-1 ); for (int i=1 ;i<=n;i++) { int sum=0 ; for (int j=0 ;j<=k;j++) sum+=f[i][j]; printf ("%d\n" ,sum); } return 0 ; }
记录一下以 i i i i i i i i i
然后进行 DFS,如果当前点是左括号,那么就更新一下最近未匹配的左括号,如果是右括号,那么合法的括号数就要加上之前已经合法的括号数再加一。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <bits/stdc++.h> using namespace std;const int N=5e5 +7 ;typedef long long ll;ll ans; int n,edcnt;int fir[N],fa[N],last[N];ll f[N]; string par; struct edge { int to,nxt; }e[N<<1 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void dfs (int u) last[u]=last[fa[u]]; if (par[u-1 ]=='(' ) last[u]=u; else if (last[u]) f[u]=f[fa[last[u]]]+1 ,last[u]=last[fa[last[u]]]; for (int i=fir[u];i;i=e[i].nxt) dfs (e[i].to); } int main () scanf ("%d" ,&n); cin>>par; for (int i=2 ;i<=n;i++) { scanf ("%d" ,&fa[i]); add (fa[i],i); } dfs (1 ); ans=f[1 ]; for (int i=2 ;i<=n;i++) f[i]+=f[fa[i]],ans^=i*f[i]; printf ("%lld" ,ans); return 0 ; }
我们考虑每条边,这条边被经过的次数乘以它的边权便是它产生的贡献,而一条边被经过的次数其实就是它左边和右边的点对数,设 f i , j f_{i,j} f i , j i i i j j j
转移时,其实就是合并子树,如果不是第一次,也就是说可以不选黑色点,要记得与该子树全为白色点取max。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 #include <bits/stdc++.h> using namespace std;const int N=2005 ;typedef long long ll;int n,k,edcnt;int fir[N],siz[N];ll f[N][N]; struct edge { int to,nxt,val; }e[N<<1 ]; void add (int u,int v,int w) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; e[edcnt].val=w; fir[u]=edcnt; } void dp (int u,int fa) siz[u]=1 ; f[u][0 ]=f[u][1 ]=0 ; for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; dp (v,u); siz[u]+=siz[v]; for (int j=min (k,siz[u]);j>=0 ;j--) { if (f[u][j]!=-1 ) f[u][j]+=f[v][0 ]+1ll *siz[v]*(n-k-siz[v])*e[i].val; for (int l=min (j,siz[v]);l>=1 ;l--) if (f[u][j-l]!=-1 ) { ll tot=(1ll *l*(k-l)+(siz[v]-l)*(n-k-siz[v]+l))*e[i].val; f[u][j]=max (f[u][j],f[u][j-l]+f[v][l]+tot); } } } } int main () scanf ("%d%d" ,&n,&k); for (int i=2 ;i<=n;i++) { int u,v,w; scanf ("%d%d%d" ,&u,&v,&w); add (u,v,w); add (v,u,w); } memset (f,-1 ,sizeof (f)); dp (1 ,-1 ); printf ("%lld" ,f[1 ][k]); return 0 ; }
定义 f i , j f_{i,j} f i , j i i i j j j
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> using namespace std;int n;double ans=0x3f3f3f3f ;struct Cheese { double x,y; }c[20 ]; double dist (Cheese a,Cheese b) return sqrt ((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } double f[1 <<16 ][18 ];int main () scanf ("%d" ,&n); for (int i=0 ;i<n;i++) scanf ("%lf%lf" ,&c[i].x,&c[i].y); memset (f,127 ,sizeof (f)); for (int i=0 ;i<n;i++) f[1 <<i][i]=dist ({0 ,0 },c[i]); for (int i=0 ;i<(1 <<n);i++) for (int j=0 ;j<n;j++) if ((i>>j)&1 ) for (int k=0 ;k<n;k++) if (((i>>k)&1 )==0 ) f[i|(1 <<k)][k]=min (f[i|(1 <<k)][k],f[i][j]+dist (c[j],c[k])); for (int i=0 ;i<=n-1 ;i++) ans=min (ans,f[(1 <<n)-1 ][i]); printf ("%.2f" ,ans); return 0 ; }
与吃奶酪类似,就是最后要回到起点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <bits/stdc++.h> using namespace std;int n;int f[(1 <<20 )+1 ][21 ];int dist[21 ][21 ];int ans=INT_MAX;int main () scanf ("%d" ,&n); for (int i=0 ;i<n;i++) for (int j=0 ;j<n;j++) scanf ("%d" ,&dist[i][j]); memset (f,0x3f ,sizeof (f)); f[1 ][0 ]=0 ; for (int i=0 ;i<(1 <<n);i++) for (int j=0 ;j<n;j++) if ((i>>j)&1 ) for (int k=0 ;k<n;k++) if (((i>>k)&1 )==0 ) f[i|(1 <<k)][k]=min (f[i|(1 <<k)][k],f[i][j]+dist[j][k]); for (int i=0 ;i<n;i++) ans=min (ans,f[(1 <<n)-1 ][i]+dist[i][0 ]); printf ("%d" ,ans); return 0 ; }
先预处理出所有能连着说的两个单词所贡献的复杂度,然后处理下只说这个单词的复杂度,然后就可以愉快地进行状压DP了,枚举每一个状态,判断下上一个是否已经选过了,只有上一个选过了才能进行转移,并且下一个要选的没有选过。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;int dist[20 ][20 ];int f[1 <<17 ][17 ];string word[17 ]; int n;int ans=-1 ;int main () scanf ("%d" ,&n); for (int i=0 ;i<n;i++) cin>>word[i]; memset (dist,0xc0 ,sizeof (dist)); for (int i=0 ;i<n;i++) for (int j=0 ;j<n;j++) if (i!=j&&word[i][word[i].length ()-1 ]==word[j][0 ]) dist[i][j]=word[j].length (); memset (f,-1 ,sizeof (f)); for (int i=0 ;i<n;i++) f[1 <<i][i]=word[i].length (); for (int i=0 ;i<(1 <<n);i++) for (int j=0 ;j<n;j++) if ((i>>j)&1 ) for (int k=0 ;k<n;k++) if (((i>>k)&1 )==0 ) f[i|(1 <<k)][k]=max (f[i|(1 <<k)][k],f[i][j]+dist[j][k]); for (int i=0 ;i<(1 <<n);i++) for (int j=0 ;j<n;j++) ans=max (ans,f[i][j]); printf ("%d" ,ans); return 0 ; }
首先把每一行的地形都预处理为一个二进制数,1代表山地,0代表平原,这样枚举每一个状态的时候,如果它们与起来的结果不是零,那么这个状态便不合法。
由于该行状态会受到上一行和上上行的影响,所以我们只需要记录本行和上一行,枚举三行的状态即可,这里需要用到滚动数组优化。
判断状态是否合法可以通过左移一位和两位与上行、上上行与来判断。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> using namespace std;int n,m,ans;int f[3 ][1 <<10 ][1 <<10 ];int mp[101 ];int sum[1 <<10 ];int main () scanf ("%d%d" ,&n,&m); for (int i=0 ;i<n;i++) for (int j=0 ;j<m;j++) { char c=getchar (); while (c!='H' &&c!='P' ) c=getchar (); mp[i]<<=1 ; mp[i]+=(c=='H' ?1 :0 ); } for (int i=1 ;i<(1 <<m);i++) { int nope=i; while (nope) { if (nope&1 ) sum[i]++; nope>>=1 ; } } for (int i=0 ;i<(1 <<m);i++) if (!((i&mp[0 ])||(i&(i<<1 ))||(i&(i<<2 )))) f[0 ][0 ][i]=sum[i]; for (int i=0 ;i<(1 <<m);i++) for (int j=0 ;j<(1 <<m);j++) if (!(i&j||i&mp[0 ]||j&mp[1 ]||(i&(i<<1 ))||(i&(i<<2 ))||(j&(j<<1 ))||(j&(j<<2 )))) f[1 ][i][j]=sum[i]+sum[j]; for (int i=2 ;i<n;i++) for (int j=0 ;j<(1 <<m);j++) if (!(j&(mp[i-1 ])||(j&(j<<1 ))||(j&(j<<2 )))) for (int l=0 ;l<(1 <<m);l++) if (!((l&j)||(l&mp[i-2 ])||(l&(l<<1 ))||(l&(l<<2 )))) for (int k=0 ;k<(1 <<m);k++) if (!((k&mp[i])||(j&k)||(l&k)||(k&(k<<1 ))||(k&(k<<2 )))) f[i%3 ][j][k]=max (f[i%3 ][j][k],f[(i-1 )%3 ][l][j]+sum[k]); for (int i=0 ;i<(1 <<m);i++) for (int j=0 ;j<(1 <<m);j++) ans=max (ans,f[(n-1 )%3 ][i][j]); printf ("%d" ,ans); return 0 ; }
与炮兵阵地类似,利用左移和右移判断状态是否合法。
由于要用完所有国王,所以要记录一下当前状态用了几个国王,预处理出来每个状态该行对应的国王数即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;typedef long long ll;int n,K;ll ans; ll f[10 ][1 <<10 ][101 ]; int sum[1 <<10 ];int main () scanf ("%d%d" ,&n,&K); for (int i=0 ;i<(1 <<n);i++) { int nope=i; while (nope) { if (nope&1 ) sum[i]++; nope>>=1 ; } } f[0 ][0 ][0 ]=1 ; for (int i=1 ;i<=n;i++) for (int j=0 ;j<(1 <<n);j++) if (!((j&(j<<1 ))||(j&(j>>1 )))) for (int k=0 ;k<(1 <<n);k++) if (!(k&(k<<1 )||(k&(k>>1 ))||(k&j)||((j>>1 )&k)||((j<<1 )&k))) for (int l=sum[k];l<=K;l++) f[i][k][l]+=f[i-1 ][j][l-sum[k]]; for (int i=0 ;i<(1 <<n);i++) if (!(i&(i<<1 )||(i&(i>>1 )))) ans+=f[n][i][K]; printf ("%lld" ,ans); return 0 ; }
记录色块可以用二维矩阵模拟。
为了防止边界计算重复,所以在二维数组中采用左开右闭的方式存储,
然后记录一下每一个矩形上方的矩阵,用来判断当前状态是否合法。
什么都没涂的时候第一次也是要拿起刷子的,注意。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 #include <bits/stdc++.h> using namespace std;struct rectangle { int topLeftX,topLeftY,bottomRightX,bottomRightY; int color; }rec[17 ]; int n;int mp[101 ][101 ];int sum[17 ];int up[17 ][17 ];int dp[1 <<16 ][21 ];bool check (int x,int y) for (int i=1 ;i<=sum[y];i++) if (!(x>>(up[y][i]-1 )&1 )) return false ; return true ; } int main () scanf ("%d" ,&n); for (int i=1 ;i<=n;i++) { scanf ("%d%d%d%d%d" ,&rec[i].topLeftY,&rec[i].topLeftX,&rec[i].bottomRightY,&rec[i].bottomRightX,&rec[i].color); for (int j=rec[i].topLeftX;j<rec[i].bottomRightX;j++) for (int k=rec[i].topLeftY;k<rec[i].bottomRightY;k++) mp[j][k]=i; } for (int i=1 ;i<=n;i++) if (rec[i].topLeftY) { int y=rec[i].topLeftY-1 ; for (int j=rec[i].topLeftX+1 ;j<=rec[i].bottomRightX;j++) if (mp[j][y]!=mp[j-1 ][y]) up[i][++sum[i]]=mp[j-1 ][y]; if (mp[rec[i].bottomRightX][y]==mp[rec[i].bottomRightX-1 ][y]) up[i][++sum[i]]=mp[rec[i].bottomRightX-1 ][y]; } memset (dp,0x3f ,sizeof (dp)); for (int i=1 ;i<=20 ;i++) dp[0 ][i]=1 ; for (int i=1 ;i<(1 <<n);i++) for (int j=1 ;j<=n;j++) if (((i>>(j-1 ))&1 )&&check (i,j)) { for (int k=1 ;k<=20 ;k++) if (k!=rec[j].color) dp[i][rec[j].color]=min (dp[i][rec[j].color],dp[i-(1 <<(j-1 ))][k]+1 ); dp[i][rec[j].color]=min (dp[i][rec[j].color],dp[i-(1 <<(j-1 ))][rec[j].color]); } int ans=0x3f3f3f5f ; for (int i=1 ;i<=20 ;i++) ans=min (ans,dp[(1 <<n)-1 ][i]); printf ("%d" ,ans); return 0 ; }
P5005中国象棋-摆上马
注意判断要进行双向判断,并不是我 i i i j j j j j j i i i
对于这种状态累加而非覆盖的滚动数组优化,一定要在更新前把旧的用不到的状态清零。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <bits/stdc++.h> using namespace std;const int mod=1e9 +7 ;typedef long long ll;int f[3 ][65 ][65 ];int n,m;ll ans; bool check_1 (int x,int y) for (int i=0 ;i<m;i++) { if (((x>>i)&1 )&&(!((x>>(i+1 ))&1 ))&&((y>>(i+2 ))&1 )) return false ; if (((x>>i)&1 )&&(!((x>>(i-1 ))&1 ))&&((y>>(i-2 ))&1 )) return false ; } return true ; } bool check_2 (int x,int y,int z) for (int i=0 ;i<m;i++) { if (((x>>i)&1 )&&(!((y>>i)&1 ))&&((z>>(i+1 ))&1 )) return false ; if (((x>>i)&1 )&&(!((y>>i)&1 ))&&((z>>(i-1 ))&1 )) return false ; } return true ; } int main () scanf ("%d%d" ,&n,&m); for (int i=0 ;i<(1 <<m);i++) f[1 ][0 ][i]=1 ; for (int i=0 ;i<(1 <<m);i++) for (int j=0 ;j<(1 <<m);j++) if (check_1 (i,j)&&check_1 (j,i)) f[2 ][i][j]=(1ll *f[2 ][i][j]+1ll *f[1 ][0 ][i])%mod; for (int i=3 ;i<=n;i++) { memset (f[i%3 ],0 ,sizeof (f[i%3 ])); for (int j=0 ;j<(1 <<m);j++) for (int k=0 ;k<(1 <<m);k++) if (check_1 (j,k)&&check_1 (k,j)) for (int l=0 ;l<(1 <<m);l++) if (check_1 (k,l)&&check_1 (l,k)&&check_2 (j,k,l)&&check_2 (l,k,j)) f[i%3 ][k][l]=(1ll *f[i%3 ][k][l]+1ll *f[(i-1 )%3 ][j][k])%mod; } for (int i=0 ;i<(1 <<m);i++) for (int j=0 ;j<(1 <<m);j++) if (check_1 (i,j)&&check_1 (j,i)) ans=(ans+1ll *f[n%3 ][i][j])%mod; printf ("%lld" ,ans%mod); return 0 ; }
首先预处理出所有长度和不同最高位的windy数方案数。
然后进行讨论即可,详情见注释。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 #include <bits/stdc++.h> using namespace std;typedef long long ll;ll f[11 ][11 ]; int numb[11 ];int a,b;void dp () for (int i=0 ;i<=9 ;i++) f[1 ][i]=1 ; for (int i=2 ;i<=11 ;i++) for (int j=0 ;j<=9 ;j++) for (int k=0 ;k<=9 ;k++) if (abs (j-k)>=2 ) f[i][j]+=f[i-1 ][k]; } ll solve (int x) ll sum=0 ; memset (numb,0 ,sizeof (numb)); int len=0 ; while (x) { numb[++len]=x%10 ; x/=10 ; } for (int i=1 ;i<=len;i++) { if (i==len) { for (int j=1 ;j<numb[len];j++) sum+=f[i][j]; break ; } for (int j=1 ;j<=9 ;j++) sum+=f[i][j]; } for (int i=len-1 ;i>=1 ;i--) { for (int j=0 ;j<numb[i];j++) if (abs (j-numb[i+1 ])>=2 ) sum+=f[i][j]; if (abs (numb[i]-numb[i+1 ])<2 ) break ; if (i==1 ) sum++; } return sum; } int main () scanf ("%d%d" ,&a,&b); dp (); printf ("%lld" ,solve (b)-solve (a-1 )); return 0 ; }
题意:求区间内满足 相邻两个数位至少差 2 的条件的数的个数。
本题有两个额外限制条件:前导零和上一个填的数,都需要记录。
注意初始 last 的初始化,不要约束到第一个数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 #include <bits/stdc++.h> using namespace std;typedef long long LL;const int INF = 1e9 ;int f[22 ][12 ]; int a[15 ];int dfs (int pos, bool limit, bool lead, int last) if (!pos) return 1 ; if (!limit && last != INF && ~f[pos][last]) return f[pos][last]; int up = limit ? a[pos] : 9 ; int res = 0 ; for (int i = 0 ; i <= up; i++) { if (lead) res += dfs (pos - 1 , limit && i == up, lead && i == 0 , i == 0 ? last : i); else if (abs (last - i) >= 2 ) res += dfs (pos - 1 , limit && i == up, false , i); } if (!limit && last != INF) f[pos][last] = res; return res; } int solve (LL x) int len = 0 ; while (x) { a[++len] = x % 10 ; x /= 10 ; } return dfs (len, true , true , INF); } int main () memset (f, -1 , sizeof (f)); LL l, r; scanf ("%lld%lld" , &l, &r); LL ans = solve (r) - solve (l - 1 ); cout << ans << endl; return 0 ; }
题意:求区间内的每个数字的每位数的数位和。
令 f p o s , s u m f_{pos,sum} f p o s , s u m [ 1 , p o s ] [1,pos] [ 1 , p o s ]
从高位向低位搜索,会出现很多重复状态。
这样的好处是让程序帮你计算后缀记忆化的量,而不是自己手推复杂的式子正向递推减小正确率。
讨论区
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #include <bits/stdc++.h> using namespace std;typedef long long LL;const int N = 1e3 ;const int MOD = 1e9 + 7 ;int f[N][N];int a[N];LL dfs (int pos, bool limit, int sum) if (!pos) return sum; if (!limit && ~f[pos][sum]) return f[pos][sum]; int up = limit ? a[pos] : 9 ; LL res = 0 ; for (int i = 0 ; i <= up; i++) res = (res + dfs (pos - 1 , limit && i == up, sum + i)) % MOD; if (!limit) f[pos][sum] = res; return res; } LL solve (LL x) int len = 0 ; while (x) { a[++len] = x % 10 ; x /= 10 ; } return dfs (len, true , 0 ); } int main () int t; scanf ("%d" , &t); memset (f, -1 , sizeof (f)); while (t--) { LL l, r; scanf ("%lld%lld" , &l, &r); LL ans = (solve (r) - solve (l - 1 ) + MOD) % MOD; printf ("%lld\n" , ans); } return 0 ; }
题意:求区间内每个数的十进制下每一位出现的次数。
这个限制条件多了一个前导零,判断一下前导零不要加到 0 的计数里即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 #include <bits/stdc++.h> using namespace std;typedef long long LL;int a[15 ];LL f[15 ][15 ][2 ]; LL ans[15 ]; int di;LL dfs (int pos, bool limit, bool lead, int cnt) if (!pos) return cnt; auto &now = f[pos][cnt][di != 0 ]; if (!limit && !lead && ~now) return now; int up = limit ? a[pos] : 9 ; LL res = 0 ; for (int i = 0 ; i <= up; i++) { int temp = cnt + (i == di); if (lead && di == 0 && i == 0 ) temp = 0 ; res += dfs (pos - 1 , limit && i == up, lead && i == 0 , temp); } if (!limit && !lead) now = res; return res; } void solve (LL x, int g) int len = 0 ; while (x > 0 ) { a[++len] = x % 10 ; x /= 10 ; } for (int i = 0 ; i <= 9 ; i++) { di = i; ans[i] += g * dfs (len, true , true , 0 ); } } int main () memset (f, -1 , sizeof (f)); LL l, r; scanf ("%lld%lld" , &l, &r); solve (r, 1 ); solve (l - 1 , -1 ); for (int i = 0 ; i <= 9 ; i++) printf ("%lld " , ans[i]); return 0 ; }
P4317花神的数论题
题意:求区间(左端点为 1)内所有数在二进制表示下 1 的个数的乘积。
本题无额外约束条件,转换为二进制进行数位 DP 即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;typedef long long LL;const int MOD = 1e7 + 7 ;LL f[82 ][111 ]; int a[82 ];LL dfs (int pos, int limit, int cnt) if (!pos) return max (cnt, 1 ); if (!limit && ~f[pos][cnt]) return f[pos][cnt]; LL res = 1 ; int up = limit ? a[pos] : 1 ; for (int i = 0 ; i <= up; i++) res = (res * dfs (pos - 1 , limit && i == up, cnt + (i & 1 ))) % MOD; if (!limit) f[pos][cnt] = res; return res; } LL solve (LL x) int len = 0 ; while (x) { a[++len] = x % 2 ; x /= 2 ; } return dfs (len, true , 0 ); } int main () memset (f, -1 , sizeof (f)); LL n; scanf ("%lld" , &n); cout << solve (n); return 0 ; }
题意:区间内满足二进制下 0 的个数不小于 1 的个数的数的方案数。
本题有两个额外约束条件:当前 0 的数目和 1 的数目和是否有前导零(因为要统计 0 的数目)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <bits/stdc++.h> using namespace std;typedef long long LL;int f[82 ][82 ][82 ]; int a[82 ];int dfs (int pos, bool limit, bool lead, int sum0, int sum1) if (!pos) return sum0 >= sum1; if (!limit && ~f[pos][sum0][sum1]) return f[pos][sum0][sum1]; int up = limit ? a[pos] : 1 ; int res = 0 ; for (int i = 0 ; i <= up; i++) { if (lead && (i == 0 )) res += dfs (pos - 1 , limit && i == up, true , 0 , 0 ); else res += dfs (pos - 1 , limit && i == up, false , sum0 + (i == 0 ), sum1 + (i == 1 )); } if (!limit) f[pos][sum0][sum1] = res; return res; } int solve (LL x) int len = 0 ; while (x) { a[++len] = x % 2 ; x /= 2 ; } return dfs (len, true , true , 0 , 0 ); } int main () memset (f, -1 , sizeof (f)); LL l, r; scanf ("%lld%lld" , &l, &r); LL ans = solve (r) - solve (l - 1 ); cout << ans << endl; return 0 ; }
题意:求区间内满足偶数位全是 d 且奇数位不是 d 且模 d 为 0 的方案数。
本体额外限制条件:模 m m m 0 0 0 l − 1 l-1 l − 1 l l l
然后注意最高位不同情况下下标也不同。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 #include <bits/stdc++.h> using namespace std;typedef long long LL;const int MOD = 1e9 + 7 ;LL f[2005 ][2005 ]; int len, m, d;int a[2005 ]; LL dfs (int pos, bool limit, int r) if (!pos) return r == 0 ; if (!limit && ~f[pos][r]) return f[pos][r]; LL res = 0 ; int up = limit ? a[pos] : 9 ; bool t = (len - pos + 1 ) & 1 ; if (t) { for (int i = 0 ; i <= up; i++) { if (i == d) continue ; res = (res + dfs (pos - 1 , limit && i == up, (r * 10 + i) % m)) % MOD; } } else { if (d <= up) res = (res + dfs (pos - 1 , limit && d == up, (r * 10 + d) % m)) % MOD; } if (!limit) f[pos][r] = res; return res; } LL solve (string x) len = x.size (); for (int i = 0 ; i < len; i++) a[len - i] = x[i] - '0' ; return dfs (len, true , 0 ); } bool check (string x) int r = 0 ; int len = x.size (); for (int i = 0 ; i < len; i++) a[i + 1 ] = x[i] - '0' ; for (int i = 1 ; i <= len; i++) { if (i & 1 ) { if (a[i] == d) return false ; } else if (a[i] != d) return false ; r = (r * 10 + a[i]) % m; } return r == 0 ; } int main () memset (f, -1 , sizeof (f)); string l, r; scanf ("%d%d" , &m, &d); cin >> l >> r; cout << (solve (r) - solve (l) + check (l) + MOD) % MOD; return 0 ; }
题意:求区间内满足限制的手机号码的个数。
本题额外限制:
最高位为 1 有三个相邻且相同的数 4 和 8 不同时出现 分别记录:
上一个数,上上个数,之前是否出现过三个相邻且相等,之前是否出现过 4,之前是否出现过 8.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 #include <bits/stdc++.h> using namespace std;typedef long long LL;int a[12 ];int len;int f[12 ][10 ][10 ][2 ][2 ][2 ]; LL dfs (int pos, int limit, int last1, int last2, bool same, bool have4, bool have8) if (!pos) return (!(have4 && have8) && same); auto &now = f[pos][last1][last2][same][have4][have8]; if (!limit && ~now) return now; LL res = 0 ; int up = limit ? a[pos] : 9 ; int down = pos == len ? 1 : 0 ; for (int i = down; i <= up; i++) { if (i == 4 && !have8) res += dfs (pos - 1 , limit && i == up, i, last1, same || (i == last1 && i == last2), true , false ); else if (i == 8 && !have4) res += dfs (pos - 1 , limit && i == up, i, last1, same || (i == last1 && i == last1 && i == last2), false , true ); else if (i != 4 && i != 8 ) res += dfs (pos - 1 , limit && i == up, i, last1, same || (i == last1 && i == last2), have4, have8); } if (!limit) now = res; return res; } LL solve (LL x) if (x < 1e10 ) return 0 ; len = 0 ; while (x) { a[++len] = x % 10 ; x /= 10 ; } return dfs (len, true , -1 , -1 , false , false , false ); } int main () LL l, r; scanf ("%lld%lld" , &l, &r); memset (f, -1 , sizeof (f)); printf ("%lld\n" , solve (r) - solve (l - 1 )); return 0 ; }
题意:求区间内的数都转换为 b 进制后,满足 [ 0 , b − 1 ] [0,b-1] [ 0 , b − 1 ]
坑点:
开 ll 记搜一定要判断前导零,只有合法的状态才可以被记忆化,而全是前导零的状态每一位都是 0,不合法所以不能被记忆化。 本题限制:一个集合内数的出现个数都为偶数次,这个可以用一个二进制数状态压缩一下,第 i 位 代表 i 这个数当前是奇数次还是偶数次。
为了可以状态复用,所以状态多记录一个当前是几进制。
注意,全是偶数,即状态压缩后结果为 0,要排除全为前导零的情况。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <bits/stdc++.h> using namespace std;typedef long long LL;int len;int a[62 ];int b;LL f[12 ][62 ][1030 ]; LL dfs (int pos, bool limit, int state, bool lead) if (!pos) return (state == 0 && !lead); auto &now = f[b][pos][state]; if (!limit && !lead && ~now) return now; LL res = 0 ; int up = limit ? a[pos] : b - 1 ; for (int i = 0 ; i <= up; i++) { res += dfs (pos - 1 , limit && i == up, (lead && i == 0 ) ? 0 : state ^ (1 << i), lead && i == 0 ); } if (!limit && !lead) now = res; return res; } LL solve (LL x) len = 0 ; while (x) { a[++len] = x % b; x /= b; } return dfs (len, true , 0 , true ); } int main () memset (f, -1 , sizeof (f)); LL l, r; int q; scanf ("%d" , &q); while (q--) { scanf ("%d%lld%lld" , &b, &l, &r); cout << solve (r) - solve (l - 1 ) << endl; } return 0 ; }
题意:求一段区间内满足限制的数。
限制:对于数的每一位出现过 的数码,偶数出现奇数次,奇数出现偶数次。
偶数要么出现零次要么出现奇数次,奇数要么出现零次要么出现偶数次。
这里由于有没出现过,奇数次,偶数次三种状态,所以一位二进制无法将其表示,因此这里用两位二进制数表示一个数的状态。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 #include <bits/stdc++.h> using namespace std;typedef long long LL;const int MOD = 1e9 + 7 ;int n, m;int a[22 ];LL f[22 ][(1 << 20 )]; bool check (int st) for (int i = 0 ; i <= 9 ; i++) { int temp = (st >> (2 * i)) & 0b11 ; if (i & 1 ) { if (temp == 0b01 ) return false ; } else if (temp == 0b10 ) return false ; } return true ; } int add (int st, int i) int temp = (st >> (2 * i)) & 0b11 ; st -= (temp << (2 * i)); if (temp == 0 ) temp = 0b01 ; else temp ^= 0b11 ; st |= temp << (2 * i); return st; } LL dfs (int pos, bool limit, bool lead, int st) if (!pos) return !lead && check (st); auto &now = f[pos][st]; if (!limit && !lead && ~now) return now; LL res = 0 ; int up = limit ? a[pos] : 9 ; for (int i = 0 ; i <= up; i++) { int temp = (lead && i == 0 ) ? 0 : add (st, i); res += dfs (pos - 1 , limit && i == up, lead && i == 0 , temp); } if (!limit && !lead) now = res; return res; } LL solve (LL x) int len = 0 ; while (x) { a[++len] = x % 10 ; x /= 10 ; } return dfs (len, true , true , 0 ); } int main () memset (f, -1 , sizeof (f)); int t; scanf ("%d" , &t); while (t--) { LL l, r; scanf ("%lld%lld" , &l, &r); printf ("%lld\n" , solve (r) - solve (l - 1 )); } return 0 ; }
题意:求有多少个长度为 k k k
a i ∈ [ 0 , m ] a_i\in[0,m] a i ∈ [ 0 , m ] ( ∑ i = 1 k ∑ j = 1 i − 1 a i ⊕ a j ) = n (\sum_{i=1}^k\sum_{j=1}^{i-1}a_i\oplus{a_j})=n ( ∑ i = 1 k ∑ j = 1 i − 1 a i ⊕ a j ) = n 异或当前位产生价值的条件是当前这位是一个 ( 0 , 1 ) (0,1) ( 0 , 1 ) 2 p o s 2^{pos} 2 p o s
由于是一个数组,假设有 y y y 2 p o s × y × ( k − y ) 2^{pos}\times{y}\times{(k-y)} 2 p o s × y × ( k − y )
由于是很多数,所以我们记录总共受到限制的数的个数 s s s
当 m m m
枚举 i , j i,j i , j s s s i i i k − s k-s k − s j j j 2 p o s × ( i + j ) × ( k − i − j ) 2^{pos}\times(i+j)\times(k-i-j) 2 p o s × ( i + j ) × ( k − i − j ) dfs(pos - 1, i, now + v)
这一位 0 时:
只需枚举 k − s k-s k − s j j j 2 p o s × j × ( k − j ) 2^{pos}\times{j}\times(k-j) 2 p o s × j × ( k − j )
下一层就是:dfs(pos - 1, s, now + v)
n o w > n now>n n o w > n
m a x + n o w < n max+now<n m a x + n o w < n
由于本题只要状态有值就均是合法的,所以都可以记忆化。
由于第三维 n o w now n o w map 存。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 #include <bits/stdc++.h> using namespace std;typedef long long LL;const int MOD = 1e9 + 7 ;map<LL, LL> f[62 ][62 ]; LL n, m; int k;LL c[62 ][62 ]; int b[62 ];void init () c[0 ][0 ] = 1 ; for (int i = 1 ; i <= 60 ; i++) { c[i][0 ] = 1 ; for (int j = 1 ; j <= i; j++) c[i][j] = (c[i - 1 ][j] + c[i - 1 ][j - 1 ]) % MOD; } } LL dfs (int pos, int s, LL now) if (now > n) return 0 ; if (pos == -1 ) return now == n; if (now + ((1ll << (pos + 1 )) - 1 ) * (k / 2 ) * (k - k / 2 ) < n) return 0 ; if (f[pos][s].count (now)) return f[pos][s][now]; LL res = 0 ; if (b[pos] == 1 ) { for (int i = 0 ; i <= s; i++) for (int j = 0 ; j <= k - s; j++) { LL v = (LL)(k - i - j) * (i + j) * (1ll << pos); LL temp = c[s][i] * c[k - s][j] % MOD; res = (res + temp * dfs (pos - 1 , i, now + v) % MOD) % MOD; } } else { for (int j = 0 ; j <= k - s; j++) { LL v = (LL)(k - j) * j * (1ll << pos); LL temp = c[k - s][j]; res = (res + temp * dfs (pos - 1 , s, now + v) % MOD) % MOD; } } f[pos][s][now] = res; return res; } LL solve (LL x) int len = 0 ; while (x) { b[len++] = x % 2 ; x /= 2 ; } return dfs (len - 1 , k, 0 ); } int main () init (); cin >> n >> m >> k; cout << solve (m) << endl; return 0 ; }
题意:求区间内各位数字之和能整除原数的数的个数。
思考一下额外限制:
前导零?没有影响。 数位之和要记录。 这个数填成什么样肯定也要记录,但是这个数会很大,状态数组肯定开不下,所以想到要模上某个数。而这个模数最好是刚好等于我们最后填完得到的数位之和,所以我们可以枚举数位之和,因为最多才 162,填完后假如填好的数是 0 (模意义下),并且模数刚好等于数位之和,那么我们就找到了一种合法状态。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <bits/stdc++.h> using namespace std;typedef long long LL;int a[22 ];int mod;LL f[22 ][170 ][170 ]; LL dfs (int pos, bool limit, int cnt, LL state) if (!pos) return (mod == cnt && state == 0 ); if (!limit && ~f[pos][cnt][state]) return f[pos][cnt][state]; int up = limit ? a[pos] : 9 ; LL res = 0 ; for (int i = 0 ; i <= up; i++) { res += dfs (pos - 1 , limit && i == up, cnt + i, (state * 10 % mod + i) % mod); } if (!limit) f[pos][cnt][state] = res; return res; } LL solve (LL x) int len = 0 ; while (x) { a[++len] = x % 10 ; x /= 10 ; } LL res = 0 ; for (mod = 1 ; mod <= len * 9 ; mod++) { memset (f, -1 , sizeof (f)); res += dfs (len, true , 0 , 0 ); } return res; } int main () LL l, r; scanf ("%lld%lld" , &l, &r); cout << solve (r) - solve (l - 1 ) << endl; return 0 ; }
题意:求一段区间内有多少数是萌数。
萌数:存在长度至少为 2 的回文子串。
所以我们只需要考虑存在多少长度为 2 或者长度为 3 的子串即可。
由于正着考虑太麻烦了 其实就是懒得考虑
所以我们反向考虑,判断这段区间内存在多少没有回文子串的数,然后取个补集即可。
我们需要记录上一个数,上上个数,以及是否处于前导零状态。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 #include <bits/stdc++.h> using namespace std;typedef long long LL;const int MOD = 1e9 + 7 ;LL f[1010 ][11 ][11 ]; int a[1010 ];string l, r; int len;bool check (string x) int le = x.length (); for (int i = 2 ; i < le; i++) if (x[i] == x[i - 1 ] || (x[i] == x[i - 2 ])) return false ; return true ; } LL dfs (int pos, bool limit, bool lead, int pre, int prpre) if (!pos) return 1 ; auto &now = f[pos][pre][prpre]; if (~now && !limit && !lead && pre != -1 && prpre != -1 ) return now; int up = limit ? a[pos] : 9 ; LL res = 0 ; for (int i = 0 ; i <= up; i++) { if (i != pre && i != prpre && !lead) { res = (res + dfs (pos - 1 , limit && i == up, false , i, pre)) % MOD; } else if (lead) { res = (res + dfs (pos - 1 , limit && i == up, i == 0 , ((i == 0 ) ? -1 : i), -1 )) % MOD; } } if (!limit && !lead && pre != -1 && prpre != -1 ) now = res; return res; } LL solve (string x) memset (f, -1 , sizeof (f)); len = x.size (); for (int i = 1 ; i <= len; i++) a[i] = x[len - i] - '0' ; return dfs (len, true , true , -1 , -1 ); } int main () cin >> l >> r; LL temp1 = 0 , temp2 = 0 ; for (auto &i : l) { temp1 = ((temp1 * 10 % MOD) + i - '0' ) % MOD; } for (auto &i : r) { temp2 = ((temp2 * 10 % MOD) + i - '0' ) % MOD; } LL temp = ((solve (r) - solve (l) + check (l) + MOD) % MOD); cout << (((temp2 - temp1 + 1 ) % MOD - temp) % MOD + MOD) % MOD << endl; return 0 ; }
上一道问题的子问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 #include <bits/stdc++.h> using namespace std;typedef long long LL;int a[22 ];LL f[22 ][10 ][10 ]; int len;LL dfs (int pos, bool limit, bool lead, int pre, int prpre) if (!pos) return 1 ; auto &now = f[pos][pre][prpre]; if (!limit && !lead && pre != -1 && prpre != -1 && ~now) return now; int up = limit ? a[pos] : 9 ; LL res = 0 ; for (int i = 0 ; i <= up; i++) { if (!lead && i != pre && i != prpre) res += dfs (pos - 1 , limit && i == up, false , i, pre); else if (lead) res += dfs (pos - 1 , limit && i == up, i == 0 , (i == 0 ) ? -1 : i, -1 ); } if (!limit && !lead && pre != -1 && prpre != -1 ) now = res; return res; } LL solve (LL x) memset (f, -1 , sizeof (f)); len = 0 ; while (x) { a[++len] = x % 10 ; x /= 10 ; } return dfs (len, true , true , -1 , -1 ); } int main () LL l, r; cin >> l >> r; cout << solve (r) - solve (l - 1 ) << endl; return 0 ; }
首先,这是棵树,对于这棵树我们进行 DFS,找到从根节点开始最长的一条链,如果可以就一直走这个链,如果有多的步数,我们在中间某个位置,每多花两步就可以多走一个点,注意与总点数取 min。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;const int N=101 ;int fir[N];int edcnt;int m,n,maxdep;struct edge { int nxt,to; }e[N<<1 ]; void add (int u,int v) e[++edcnt].to=v; e[edcnt].nxt=fir[u]; fir[u]=edcnt; } void dfs (int u,int fa,int dep) maxdep=max (maxdep,dep); for (int i=fir[u];i;i=e[i].nxt) if (e[i].to!=fa) { int v=e[i].to; dfs (v,u,dep+1 ); } } int main () scanf ("%d%d" ,&m,&n); for (int i=1 ;i<=m-1 ;i++) { int a,b; scanf ("%d%d" ,&a,&b); add (a,b); add (b,a); } dfs (0 ,-1 ,0 ); if (n<=maxdep) printf ("%d" ,n+1 ); else printf ("%d" ,min (m,maxdep+1 +(n-maxdep)/2 )); return 0 ; }
题意:
给定一个长度为 n n n n n n s s s
1 l r,表示将 l ≤ i ≤ r l \le i \le r l ≤ i ≤ r s i s_i s i 0 0 0 1 1 1 1 1 1 0 0 0 2 g( g ∈ { 0 , 1 } ) (g\in \{0,1\}) ( g ∈ { 0 , 1 } ) s i = g s_i=g s i = g a i a_i a i 1 ≤ n ≤ 1 0 5 , 1 ≤ t ≤ 1 0 4 1\le n\le 10^5,1\le t\le 10^4 1 ≤ n ≤ 1 0 5 , 1 ≤ t ≤ 1 0 4
首先记录下初始时所有 1 位置的异或和,记为 ans1,记录所有 0 位置的异或和,记为 ans0,然后对于每一个 1 操作,我们都要对 ans1 和 ans0 进行异或一个区间和,而这个区间和可以通过预处理前缀异或和来解决。
这里熟悉一下 bitset 的使用。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #include <bits/stdc++.h> using namespace std;const int N = 1e5 + 7 ;typedef long long LL;int main () int t; scanf ("%d" , &t); while (t--) { LL ans0 = 0 , ans1 = 0 ; int n, q; LL sum[N] = {0 }; string s; int a[N]; scanf ("%d" , &n); for (int i = 1 ; i <= n; i++) scanf ("%d" , &a[i]), sum[i] = sum[i - 1 ] ^ a[i]; cin >> s; reverse (s.begin (), s.end ()); bitset<N> a2 (s) ; for (int i = a2. _Find_first(); i != a2. size (); i = a2. _Find_next(i)) ans1 ^= a[i + 1 ]; ans0 = sum[n] ^ ans1; scanf ("%d" , &q); while (q--) { int op; scanf ("%d" , &op); if (op == 1 ) { int l, r; scanf ("%d%d" , &l, &r); ans0 ^= sum[r] ^ sum[l - 1 ]; ans1 ^= sum[r] ^ sum[l - 1 ]; } else { int k; scanf ("%d" , &k); if (k == 0 ) cout << ans0 << ' ' ; else cout << ans1 << ' ' ; } } puts ("" ); } return 0 ; }
设他在 i 1 , i 2 , i 3 , … , i k i_1,i_2,i_3,\dots,i_k i 1 , i 2 , i 3 , … , i k
\begin{gather} a_{i_1}-d\cdot{i_1}+a_2-d\cdot(i_2-i_1)+\dots+a_{i_k}-d\cdot(i_k-i_{k-1})\\=(a_{i_1}+a_{i_2}+\dots+a_{i_k})-d\cdot{i_{k}} \end{gather}
所以就可以枚举最后一天去看的电影,然后记录前 m − 1 m-1 m − 1 multiset 维护即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <bits/stdc++.h> using namespace std;const int N = 2e5 + 7 ;int n, m, d;int main () int t; scanf ("%d" , &t); while (t--) { int a[N], ans = 0 ; scanf ("%d%d%d" , &n, &m, &d); for (int i = 1 ; i <= n; i++) scanf ("%d" , &a[i]); set<pair<int , int > > s; int sum = 0 ; for (int i = 1 ; i <= n; i++) { int cur = sum + a[i] - d * i; ans = max (ans, cur); if (a[i] > 0 ) { s.insert ({a[i], i}); sum += a[i]; if ((int )s.size () >= m) { sum -= (*s.begin ()).first; s.erase (s.begin ()); } } } printf ("%d\n" , ans); } return 0 ; }
经典构造题。
我们为每个位置定义两种状态:必胜状态和必败状态;
必胜状态:在它前面可以选择的状态都是必败状态。 必败状态:前面没有可以选择的状态或者前面存在可以选择的必胜状态。 然后我们判断状态时只需要判断是否前面有最小的必胜状态即可,因为假如最小的必胜状态都大于当前状态,那么当前位置的前面不存在可选的必胜状态。
然后线性递推即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <bits/stdc++.h> using namespace std;const int N = 3e5 + 7 ;int main () int t; scanf ("%d" , &t); while (t--) { int n; int p[N]; scanf ("%d" , &n); for (int i = 1 ; i <= n; i++) { scanf ("%d" , &p[i]); } int ans = 0 ; int w = n + 1 , ww = n + 1 ; for (int i = 1 ; i <= n; i++) { if (w < p[i] && p[i] < ww) { ans++; ww = p[i]; } w = min (w, p[i]); } cout << ans << endl; } }