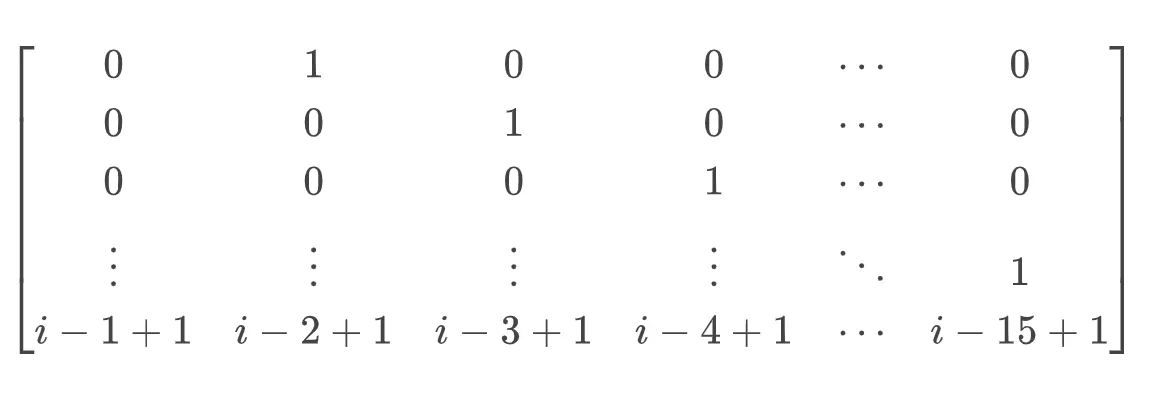ZR 七连测

Falling_Sakura
  2023-09-03 07:57:34 2023-09-03 07:57:34 Created   2025-09-24 10:27:43 2025-09-24 10:27:43 Updated    3.6k Words  16 Mins  

Day 1

T1

一道二维前缀和。

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<bits/stdc++.h>
using namespace std;
const int N=2005;
int mp[N][N];
int sum[N][N];
int sumRigh[N][N],sumDown[N][N];
char a[N][N];
string s[N];
int main()
{
    // freopen("E:/下载/Compressed/problem_2633/ex_A2.in","r",stdin);
    int n, m, h, w, k;
    scanf("%d%d%d%d%d",&n,&m,&h,&w,&k);
    for(int i = 1; i <= n; ++i)
    {
        scanf("%s\n", a[i] + 1);
        s[i] = a[i];
    }
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j) // 每个点只看它的右边和下边
        {
            // if(i - 1 >= 1) a[i][j] += (a[i-1][j]!=a[i][j]);
            // if(j - 1 >= 1) a[i][j] += (a[i][j-1]!=a[i][j]);
            if(i + 1 <= n) mp[i][j] += (a[i + 1][j] != a[i][j]);
            if(j + 1 <= m) mp[i][j] += (a[i][j + 1] != a[i][j]);
        }
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j) // 每个点只看它的右边和下边
        {
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mp[i][j]; // printf("sum[%d][%d] = %d\n", i, j, sum[i][j])
            if(a[i][j] != a[i + 1][j] && i + 1 <= n) sumDown[i][j] = sumDown[i][j - 1] + 1; // 下面总和
            else sumDown[i][j] = sumDown[i][j - 1];
        }
    for(int j = 1; j <= m; ++j)
        for(int i = 1; i <= n; ++i)
        {
            if(a[i][j] != a[i][j + 1] && j + 1 <= m) sumRigh[i][j] = sumRigh[i - 1][j] + 1; // 右边总和
            else sumRigh[i][j] = sumRigh[i - 1][j];
            // printf("sum[%d][%d] = %d\n",i,j,sumRigh[i][j]);
        }
    int now = 0,ans = 0;
    int x1, y1, x2, y2;
    for(int i = 1; i + h - 1 <= n; ++i)
        for(int j = 1; j + w - 1 <= m; ++j)
        {
            x1 = i;
            y1 = j;
            x2 = i + h - 1;
            y2 = j + w - 1;
            now = sum[x2][y2] + sum[x1 - 1][y1 - 1] - sum[x1 - 1][y2] - sum[x2][y1 - 1];
            // for(int l = y1; l <= y2; l++) // 最后一行
            //     if(a[x2][l] != a[x2 + 1][l] && x2 + 1 <= n) now--;
            now -= sumDown[x2][y2] - sumDown[x2][y1 - 1];
            now -= sumRigh[x2][y2] - sumRigh[x1 - 1][y2];
            // for(int l = x1; l <= x2; l++)
            //     if(a[l][y2] != a[l][y2 + 1] && y2 + 1 <= m) now--;
            if(now >= k) ans++;
        }
    printf("%d", ans);
    return 0;
}

T2

image.png

记 bib_i 为 aia_{i} 和 ai−1a_{i-1} 之间需要共同减掉的次数，那么就要满足 bi−1+bi=aib_{i-1}+b_i=a_i。

然后考虑每个 bib_i，把它变成一个 ±b0+c\pm b_0+c 的形式，如果 nn 是奇数，那么 bn−1=b0+cb_{n-1}=b_0+c ，然后 b0+bn−1=kb_0+b_{n-1}=k，这样就可以解出 b0b_0 ，然后求其它的 bib_i，如果算出有结果小于零或者是小数，那就是无解，否则有解。

如果 nn 是偶数，这时候 bn−1=−b0+cb_{n-1}=-b_0+c，b0+bn−1=kb_0+b_{n-1}=k，这时候如果带入的话就会都消掉什么也解不出来，这时候 cc 和 kk 是相同的，

±bi=b0+c,bi≥0\pm b_i=b_0+c,b_i\ge0 这样就可以把 b0b_0 解出一个范围，如果这个范围内有非负整数解的话，那就满足条件，否则无解。

考场就写了个 sumsum 是否为偶数的特判🤣。

T3

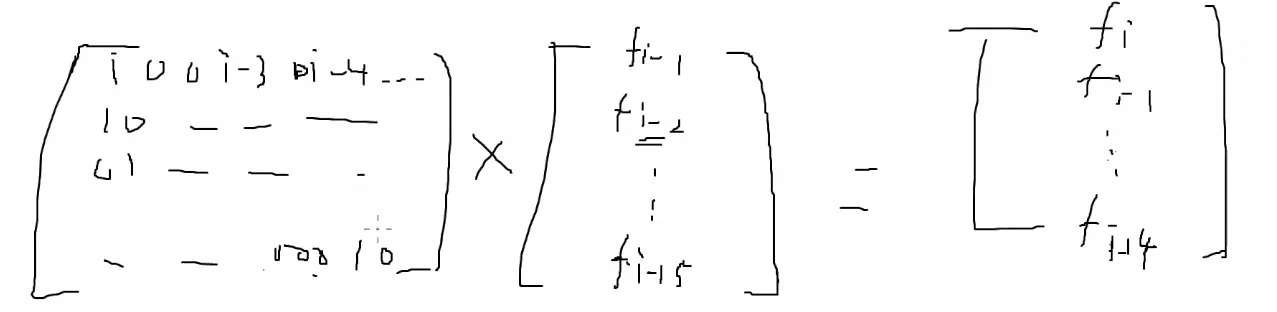
image.png

fi=∑j∈Sfi−j×(i−j+1)f_i=\sum_{j\in S} f_{i-j}\times (i-j+1)，可以用矩阵乘法维护这个十五行的矩阵。

考虑构造左边的矩阵，

比如 1 存在的话，那么第一行第一列就是 ii，因为 fi=fi−1×if_i=f_{i-1}\times i。

然后存在的话就填 i−k+1i-k+1 ，不然就填 0，然后下面几行该位存在就往后填一位 1，这样就可以保证递推。

image.png

这时候可以尝试使用矩阵快速幂，但是这里的每次要乘的矩阵都不相同，所以不可以通过矩阵乘法来维护，但是这个模数非常特殊，比较小，如果在矩阵里把每个数都模一个 2027，这个矩阵第一行其实是循环的，下面是不变的，nn 很大的情况下会形成很多个循环节，每个对应一个矩阵乘法，然后后面可能会剩一些，但也不会超过 2027。

09XDUSI%$7_RX3%Y1K2(NYS.png

由于矩阵乘法满足结合律，所以可以先处理一段循环节，然后再处理矩阵快速幂，最后再加上多出来的矩阵。

递推式也可以写成：

fi=i×∑fi−jf_i=i\times{\sum f_{i-j}}

如果这样递推出来的话就是 fnn\dfrac{f_{n}}{n}，因为最后一个不需要考虑，

但是如果 nn 是 2027 的倍数的话，就不能直接推到第 nn 项，需要求出 n−1n-1 项再求第 nn 项。

考场代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 2027;
const int N = 1e8 + 3e7;
ll f[N];
vector<int> s;
int main()
{
    // freopen("E:/下载/Compressed/problem_2635/ex_C2.in","r",stdin);
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i = 1; i <= m; ++i)
    {
        int a;
        scanf("%d",&a);
        s.emplace_back(a);
    }
    sort(s.begin(),s.end());
    f[0] = 1;
    for(int i = 0; i <= n; ++i)
    {
        for(auto &j : s)
        {
            int v = i + j;
            if(v > n) continue;
            f[v] += f[i] * (i + 1) % mod;
        }
    }
    printf("%lld", (f[n] % mod));
    return 0;
}

我这样递推最后就不用乘以一个 nn。

T4

二分答案

往里放数，使得每两个数之间的差都小于等于 kk 是否可行。

每个数可以往左放和往右放，肯定是把这个序列分成好多段，一些是往左放一些是往右放，所以每一段就可以用 RMQ 求一个差的最大值，由于分界点的位置知道，剩下的东西就很好维护，而且相邻两个分界点的数差也不能超过 kk。

记 dpidp_i 表示以 ii 和 i+1i+1 为一个分界点时是否可行。

它可以从前面最远的一个 jj 满足 fj=1f_j=1 转移而来，

这个 jj 要满足 j∼ij\sim{i} 这些数的差的最大值小于等于 kk。

并且 aj−ai+1≤xa_j-a_{i+1}\le{x}，这是因为可以把原序列分为若干段，要么是左要么是右，两个相邻的分界点由于是放在同一端，所以它们的端点之间也需要满足条件。

满足条件的 aja_j 是一段区间，也就是 ai+1−k∼ai+1+ka_{i+1}-k\sim{a_{i+1}+k}。

而满足以 ii 为右端点的后缀且满足这段后缀最大差小于等于 kk 可以用倍增求出最小的 jj ，然后用线段树维护合法的分界点，查询 aja_j 在某段区间中 jj 的最大值即可。

但是由于常数问题，会被卡到 80 分。

一百分：

image.png

实际上就是没有放，只是不断扩展这两段区间，每次判断一下范围即可。

不会编了。

考场代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 7;

int n;
int a[N];

bool check(int x)
{
    deque<int> q;
    q.push_back(a[1]);
    for(int i = 2; i <= n; ++i)
    {
        if(a[i] - q.front() <= a[i] - q.back())
        {
            if(a[i] - q.back() <= x) q.push_back(a[i]);
            else if(a[i] - q.front() <= x) q.push_front(a[i]);
            else return false;
        }
        else if(a[i] - q.front() > a[i] - q.back())
        {
            if(a[i] - q.front() <= x) q.push_front(a[i]);
            else if(a[i] - q.back() <= x) q.push_back(a[i]);
            else return false;
        }
    }
    return true;
}
int main()
{
    // freopen("E:/下载/Compressed/problem_2636/ex_D2.in","r",stdin);
    scanf("%d", &n);
    int l = 0,r = 0;
    int minn = 0x3f3f3f3f,maxn = -1;
    for(int i = 1; i <= n; ++i)
    {
        scanf("%d", &a[i]);
        minn = min(minn, a[i]);
        maxn = max(maxn, a[i]);
    }
    r = maxn - minn;
    while(l < r)
    {
        int mid = (l + r) >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    printf("%d", r);
    return 0;
}

用了一个 deque 进行贪心模拟，甚至有 55 分。

Day2

T1

image.png

题意简化：

给你一个序列，问有多少对数在模 200 意义下相等。

那就对 0∼2000\sim200 内每一个数建一个桶，答案就是 ∑i=1n(i2)\sum_{i=1}^n {i\choose2}。

记得开 long long。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 7;
typedef long long ll;

int a[N];
ll ans;
int sum[N][205];
ll c[N][3];

void init()
{
    for(int i = 2; i <= 200000; ++i)
        c[i][2] = 1ll * i * (i - 1) / 2;
}

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
    {
        scanf("%d", &a[i]);
        if(a[i] < 0) a[i] += ((-a[i]/200)+1)*200;
        a[i] %= 200;
        sum[i][a[i]]++;
    }
    init();
    for(int j = 0; j < 200; j++)
        for(int i = n; i >= 1; --i) 
            sum[i][j] += sum[i + 1][j];
    for(int i = 0; i < 200; ++i)
        ans += c[sum[1][i]][2];
    printf("%lld\n", ans);
    return 0;
}

T2

image.png

考虑贪心做法：

最小：

从左往右考虑，这个人如果左边右边还有自己的位置都没有人，那么肯定是往右会更优，因为往右可能会与下一个人相遇，而往左或者不动概率就会小。

而对于周围有人的情况，那就直接过去即可。

最多：

最少的时候我们尽量让一个周围都没人的人往右靠，那么最多与他相反，在不与他人重合的情况下，优先往左靠。

DP 的话那就令 fi,0/1/2f_{i,0/1/2} 代表考虑完了前 ii 个位置并且第 ii 个位置是向左/不动/向右，的最小/最大房屋数，本人当时就这么写的但是转移方程看上去很麻烦就没有信心推下去，写了一半 DP 一半贪心，光荣挂分。

T3

CF1735C

image.png

有两个串 SS 和 TT， 存在 S→TS\to T 的一个映射关系，映射关系为字母之间的一个环，大小为 26。

现在给定 TT， 求字典序最小的 SS。

可以考虑贪心的做法，从前往后遍历，对于每个第一次出现的字母，寻找它对应的合法的且字典序最小的一个映射。

这里合法指的是不能提前形成环，也就是不能在大小 <26<26 之前就形成了环，比如 ab\text{ab} 不能与 ba\text{ba} 建立一个映射关系，因为如果这样 aa 就是 bb 的下一个，bb 也是 aa 的下一个，这样就构成了一个二元环，其它元素没有办法插入，也就不合法。

当前环的大小可以每次向前跳统计长度，也可以通过并查集维护大小。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+7;

char s[N];
map<char,char> mp, az;

int main()
{
	int T;
	scanf("%d", &T);
	while(T--)
	{
		int n;
		scanf("%d", &n);
		scanf("%s", s + 1);
		mp.clear();
		az.clear();
		for(int i = 1; i <= n; i++) // 为每个字符寻找映射
		{
			if(mp[s[i]]) printf("%c", mp[s[i]]);
			else
			{
				for(char t= 'a' ; t <= 'z'; t++)
				{
					if(t == s[i]) continue;
					if(!az[t]) // t还没有映射对象
					{
						char tt = t;
						int cnt = 0; 
						while(tt && tt != s[i])
						{
							cnt++;
							tt=mp[tt]; 
						}
						if(tt == s[i] && cnt < 25) continue; // 判断不合法情况
						printf("%c", t); // 可以的话那么t就是字典序最小的映射
						mp[s[i]] = t;
						az[t] = mp[s[i]];
						break;
					}
				}
			}
		}
		printf("\n");
	}
	return 0;
}

T4

image.png

首先暴力可以想到跑 Floyed 全源最短路，枚举一个中间点，复杂度 O(n3)O(n^3)

1→u1\to u 的路径其实分为两段，1→p+u→p1\to p+u\to p，我们要求这个路径的最小值，

由于后半部分边是反向的，所以我们可以建反向图（分层图），然后在原图和反向图之间两个编号相同的点之间建立一条边权为 0 的边，然后以原图的 1 号点为原点，以反向图中的每一个点为终点跑最短路即可。

复杂度就是 Dijkstra 的复杂度。

Day3

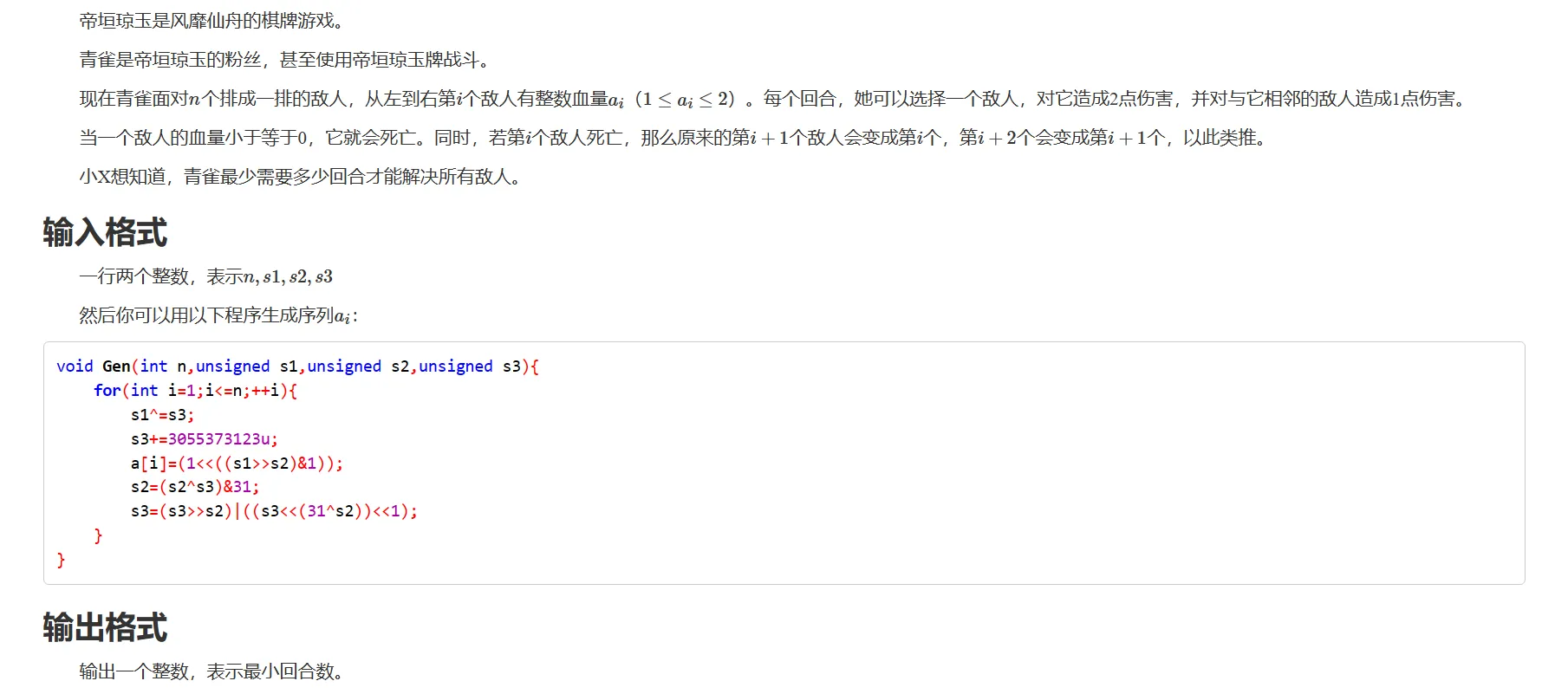
T1

image.png

随便手搓几个样例我们发现这个序列里只有 1 和 2。

那么思路就是：

从左向右遍历区间，记录 1 的个数，找出所有 2 的连续区间，如果这个区间的长度是奇数，那么就把答案加上 (len+1)/2(len+1)/2，同时判断左端点的左边是否为 1，如果是，就要把它减去，然后把这一位的 1 给减去。

如果这个 2 的区间长度是奇数，那么就把答案加上 len/2len/2，同时判断左端点的左边 1 给减去，同时把 1 的个数加一，因为我们把最后一个二看成 1，减去以后它相当于不变，也就是把这个 2 给变成 1。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<bits/stdc++.h>
using namespace std;
const int N = 3e7 + 7;
typedef long long ll;


// int a[] = {0, 1, 2, 2, 1, 2, 2, 2, 1};
int a[N];
int n, s1, s2;
ll s3;

void Gen(int n, unsigned s1, unsigned s2, unsigned s3)
{
    for(int i = 1; i <= n; ++i){
        s1 ^= s3;
        s3 += 3055373123u;
        a[i] = (1 << ((s1 >> s2) & 1));
        s2 = (s2 ^ s3) & 31;
        s3 = (s3 >> s2) | ((s3 << (31 ^ s2)) << 1);
    }
}

int main()
{
    scanf("%d%d%d%lld", &n, &s1, &s2, &s3);
    Gen(n, s1, s2, s3);
    int l = 0, r = 0;
    int sum1 = 0;
    ll ans = 0;
    bool fir = true;
    for(int i = 1; i <= n; ++i)
    {
        if(a[i] == 2)
        {
            if(fir)
            {
                fir = false;
                l =  r = i;
            }
            else
            {
                r = i;
            }
        }
        if(a[i] == 1)
        {
            sum1++;
        }
        if((a[i] == 1 || i == n) && !fir) // 结束一段 2 的区间
        {
            fir = true;
            int len = r - l + 1;
            if(len & 1)
            {
                ans += (len + 1) / 2;
                if(a[l - 1] == 1) sum1--;
                if(a[i] == 1) sum1--;
            }
            else
            {
                ans += len / 2;
                if(a[l - 1] == 1) sum1--;
                sum1++;
            }
        }
    }
    ans += (sum1 + 2) / 3;
    // printf("%d\n", sum1);
    printf("%lld", ans);
    return 0;
}

// 1 2 2 1 1 ans = 2
// 1 2 2 1 1 1 2 2 2 1 ans = 4
// 2 2 2 2 ans = 3
// 1 2 2 1 2 2 2 1 ans = 4

T2

一眼最短路

T3

T4

Day4

T1

image.png

普通攻击给到血量最小的，再现攻击给到血量最大的。

有个东西叫做 [[数据结构#Multiset|multiset]]，可以在 log 的时间内维护一个有序的序列。

T2

T3

T4

  • Title: ZR 七连测
  • Author: Falling_Sakura
  • Created at : 2023-09-03 07:57:34
  • Updated at : 2025-09-24 10:27:43
  • Link: https://vercel.fallingsakura.top/6289c257.html
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
ZR 七连测
  1. 1. Day 1
    1. 1.1. T1
    2. 1.2. T2
    3. 1.3. T3
    4. 1.4. T4
  2. 2. Day2
    1. 2.1. T1
    2. 2.2. T2
    3. 2.3. T3
    4. 2.4. T4
  3. 3. Day3
    1. 3.1. T1
    2. 3.2. T2
    3. 3.3. T3
    4. 3.4. T4
  4. 4. Day4
    1. 4.1. T1
    2. 4.2. T2
    3. 4.3. T3
    4. 4.4. T4