数据结构

Falling_Sakura
  2023-06-23 19:16:50 2023-06-23 19:16:50 Created   2025-09-25 10:18:02 2025-09-25 10:18:02 Updated   15.9k Words  79 Mins  

前言

注意对于所有的数据结构，遍历前一定要检查是否为空，或者有无可能访问到空节点。

链表

动态链表

略。

静态链表

以P1996约瑟夫问题为例

手写静态链表:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
struct node{
    int id,next,pre;
    int date;
}nodes[N];
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    nodes[0].next=1;
    for(int i=1;i<=n;i++)
    {
        nodes[i].id=i;
        nodes[i].pre=i-1;
        nodes[i].next=i+1;
    }
    nodes[n].next=0;
    nodes[0].pre=n;
    int now=0;
    while(n--)
    {
        for(int i=1;i<m;i++)
            now=nodes[now].next;
        printf("%d",nodes[now].id);
        int prev=nodes[now].pre.nex=nodes[now].next;
        nodes[prev].next=nodes[now].next;
        nodes[nex].pre=nodes[now].pre;
        now=nex;
    }
    printf("%d",nodes[now].next);
    return 0;
}

队列

以P1540机器翻译为例

手写队列

双端队列和单调队列

Deque

这里以P1886滑动窗口举例

操作作用
dq[i]返回队列中下标为i的元素
dq.front()返回队头
dq.back()返回队尾
dq.pop_front()删除队头
dq.pop_back删除队尾
dq.push_back(e)在队尾添加一个元素e
dq.push_front(e)在队头添加一个元素e
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int a[N];
deque<int> q;
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
    {
        while(!q.empty()&&a[q.back()]>a[i]) q.pop_back();
        q.push_back(i);
        if(i>=m)
        {
            while(!q.empty()&&q.front()<=i-m) q.pop_front();
            printf("%d ",a[q.front()]);
        }
    }
    puts("");
    while(!q.empty()) q.pop_front();
    for(int i=1;i<=n;i++)
    {
        while(!q.empty()&&a[q.back()]<a[i]) q.pop_back();
        q.push_back(i);
        if(i>=m)
        {
            while(!q.empty()&&q.front()<=i-m) q.pop_front();
            printf("%d ",a[q.front()]);
        }
    }
    puts("");
    return 0;
}

例题Max sum:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    scanf("%d",&t);
    for(int l=1;l<=t;l++)
    {
        int n;
        scanf("%d",&n);
        int maxsum=INT_MIN,sum=0;
        int st=1,en=1,p=1;
        for(int i=1;i<=n;i++)
        {
            int s;
            scanf("%d",&s);
            sum+=s;
            if(sum>maxsum)
            {
                maxsum=sum;
                st=p;
                en=i;
            }
            if(sum<0)
            {
                sum=0;
                p=i+1;
            }
        }
        printf("Case %d:\n",l);
        printf("%d %d %d\n",maxsum,st,en);
        if(l!=t) puts("");
    }
    return 0;
}

DP优化

P1725

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+10;
int n,l,r;
int a[N];
int f[N];
int q[N];
signed main()
{
    memset(f,128,sizeof(f));
    f[1]=0;
    scanf("%lld%lld%lld",&n,&l,&r);
    for(int i=1;i<=n+1;i++)
        scanf("%lld",&a[i]);
    int h=1,t=0,ans=-0x7ffffffff;
    for(int i=l+1;i<=n+1;i++)//l+1左边的格子跳不到
    {
        while(h<=t&&q[h]<i-r) h++;//删头
        while(h<=t&&f[q[t]]<f[i-l]) t--;//把小于当前新加的值的尾部都去掉
        q[++t]=i-l;//将最右端加入队尾
        f[i]=f[q[h]]+a[i];
        if(i+r>n+1) ans=max(ans,f[i]);
    }
    printf("%lld",ans);
    return 0;
}

栈

单调栈

以例题P2947为例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
using namespace std;
int h[200005],ans[200005];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&h[i]);
    }
    stack<int> st;
    for(int i=n;i>=1;i--)
    {
        while(!st.empty()&&h[st.top()]<=h[i]) st.pop();//比它矮的全部出栈
        //因为倒着遍历，所以新入栈的一定更靠左更靠前也更矮更有可能是更优解
        if(st.empty()) ans[i]=0;//右边没有奶牛比它高
        else ans[i]=st.top();//最近的且比它高的
        st.push(i);//入栈
    }
    for(int i=1;i<=n;i++)
    {
        printf("%d\n",ans[i]);
    }
    return 0;
}

习题P5788:

这里贴一份手写栈的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<bits/stdc++.h>
using namespace std;
int n,a[3000055],f[3000055];
struct fstack{//手写栈
    int w[3000055];
    int t=0;//栈顶位置
    void push(int x)//插入
    {
        w[++t]=x;
    }
    int top()//返回顶部值
    {
        return w[t];
    }
    void pop()//弹出栈顶
    {
        t--;
    }
    bool empty()//判断是否为空
    {
        return t==0;
    }
}s;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=n;i>=1;i--)
    {
        while(!s.empty()&&a[i]>=a[s.top()]) s.pop();
        if(s.empty()) f[i]=0;
        else f[i]=s.top();
        s.push(i);
    }
    for(int i=1;i<=n;i++)
    {
        printf("%d ",f[i]);
    }
    return 0;
}
// #include<bits/stdc++.h>
// using namespace std;
// int n,a[300005],f[300005];
// int main()
// {
//     scanf("%d",&n);
//     stack<int> s;
//     for(int i=1;i<=n;i++)
//         scanf("%d",&a[i]);
//     for(int i=n;i>=1;i--)
//     {
//         while(!s.empty()&&a[i]>=a[s.top()]) s.pop();
//         if(s.empty()) f[i]=0;
//         else f[i]=s.top();
//         s.push(i);
//     }
//     for(int i=1;i<=n;i++)
//     {
//         printf("%d ",f[i]);
//     }
//     return 0;
// }

习题P1449：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
using namespace std;
#define int long long
signed main()
{
    string s;
    cin>>s;
    stack<int> st;
    for(int i=0;s[i]!='@';i++)
    {
        int now=0;
        while(s[i]>='0'&&s[i]<='9')
        {
            now*=10;
            now+=s[i]-'0';
            i++;
        }
        if(s[i]=='.')
        {
            st.push(now);
            now=0;
            continue;
        }
        if(s[i]=='+')
        {
            int a=st.top();
            st.pop();
            a+=st.top();
            st.pop();
            st.push(a);
            continue;
        }
        if(s[i]=='-')
        {
            int a=-st.top();
            st.pop();
            a+=st.top();
            st.pop();
            st.push(a);
            continue;
        }
        if(s[i]=='*')
        {
            int a=st.top();
            st.pop();
            a*=st.top();
            st.pop();
            st.push(a);
            continue;
        }
        if(s[i]=='/')
        {
            int a=st.top(),b;
            st.pop();
            b=st.top();
            st.pop();
            st.push(b/a);
        }
    }
    printf("%d",st.top());
    return 0;
}

习题P1981:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
#define int long long
signed main()
{
    stack<int> s;
    int a,b;
    char c;
    cin>>a;
    int m=10000;
    a=a%m;
    s.push(a);
    while(cin>>c>>b)
    {
        if(c=='*')
        {
            a=s.top();
            s.pop();
            s.push(a*b%m);
        }
        else    s.push(b);
    }
    a=0;
    while(s.size())
    {
        a+=s.top();
        s.pop();
        a%=m;
    }
    cout<<a<<endl;
    return 0;
}

习题P1175:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include<bits/stdc++.h>
using namespace std;
#define ll long long
/*懒得写了，目前进度走到将前缀表达式转为中缀表达式，但是同运算级并没有按照题目顺序*/
/*40%*/
struct fstack{//手写栈
    char w[30005];
    int t=0;//栈顶位置
    void push(int x)//插入
    {
        w[++t]=x;
    }
    char top()//返回顶部值
    {
        return w[t];
    }
    void pop()//弹出栈顶
    {
        t--;
    }
    bool empty()//判断是否为空
    {
        return t==0;
    }
}st,bas;
signed main()
{
    //st;//存放待处理符号
    //bas;//存放表达式
    char c;
    while((c=getchar())!=EOF)
    {
        if(c>='0'&&c<='9')
        {
            bas.push(c);
            continue;
        }
        if(c=='(')
        {
            st.push(c);
            continue;
        }
        if(c==')')
        {
            while(st.top()!='(')
            {
                bas.push(st.top());
                st.pop();//弹出(
            }
            st.pop();
            continue;
        }
        if(c=='^'&&(st.empty()||st.top()=='('))
        {
            st.push(c);
            continue;
        }
        else if(c=='^')
        {
            while((c=='^'&&(st.empty()||st.top()=='('))==false)
            {
                bas.push(st.top());
                st.pop();
            }
            st.push(c);
            continue;
        }
        if((c=='*'||c=='/')&&(st.empty()||st.top()=='('||st.top()!='^'))
        {
            st.push(c);
            continue;
        }
        else if(c=='*'||c=='/')
        {
            while(((c=='*'||c=='/')&&(st.empty()||st.top()=='('||st.top()!='^'))==false)
            {
                bas.push(st.top());
                st.pop();
            }
            st.push(c);
            continue;
        }
        if((c=='+'||c=='-')&&(st.empty()||st.top()=='('||(st.top()!='^'&&st.top()!='*'&&st.top()!='/')))
        {
            st.push(c);
            continue;
        }
        else if(c=='+'||c=='-')
        {
            while(((c=='+'||c=='-')&&(st.empty()||st.top()=='('||(st.top()!='^'&&st.top()!='*'&&st.top()!='/')))==false)
            {
                bas.push(st.top());
                st.pop();
            }
            st.push(c);
            continue;
        }
    }
    while(!st.empty())
    {
        bas.push(st.top());
        st.pop();
    }
    while(!bas.empty())
    {
        cout<<bas.top();
        bas.pop();
    }
    return 0;
}

这个大模拟作者有时间再补。

STL

Vector

#include<vector>
链接

初始化

若类型为int，则初始化为0.

若类型为string，则初始化为空字符串。

1
vector<int> a(10);//初始化了一个有十个元素的vector，且十个元素的值都是0
1
vector<int> a(10,1);//初始化了一个有十个元素的vector，且十个元素的值都是1
1
vector<int> b(a);//将a复制一份给b
1
copy(b.begin(),b.end().a.begin())//将从b.begin开始到b.end()结束的元素复制到从a.begin()开始的地方若超出则停止
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;
vector<int> a(10);
int cnt;
int main()
{

    for(auto &i:a)
    {
        i++;
        cnt++;
        // cout<<i<<endl;
    }
    vector<int> b(a);
    auto it=b.begin();
    advance(it,6);
    b.insert(it,6,6);
    copy(b.begin(),b.end(),a.begin());
    for(auto &i:a)
        cout<<i<<endl;
    cout<<cnt;
    return 0;
}

输出：

image.png

添加元素

1
2
b.push_back(i);
b.push_back({1,2});//pair

对于已存在的元素，可以像数组一样通过下标进行访问和修改。

或者：

1
2
b.emplace_back(i);
b.emplace_back(1,2);//pair

emplace 比 push 少了拷贝的过程，直接在容器尾部创建元素，因此速度更快。

插入元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream> 
#include <vector> 
#include <array> 
using namespace std;
int main()
{
    std::vector<int> demo{1,2};
    //第一种格式用法
    demo.insert(demo.begin() + 1, 3);//{1,3,2}
 
    //第二种格式用法
    demo.insert(demo.end(), 2, 5);//{1,3,2,5,5}
 
    //第三种格式用法
    std::array<int,3>test{ 7,8,9 };
    demo.insert(demo.end(), test.begin(), test.end());//{1,3,2,5,5,7,8,9}
 
    //第四种格式用法
    demo.insert(demo.end(), { 10,11 });//{1,3,2,5,5,7,8,9,10,11}
 
    for (int i = 0; i < demo.size(); i++) {
        cout << demo[i] << " ";
    }
    return 0;
}
1
b.insert(it,6,6);

在迭代器it的位置后插入66个66。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
vector<int> a(10);
int cnt;
int main()
{

    for(auto &i:a)
    {
        i++;
        cnt++;
        // cout<<i<<endl;
    }
    vector<int> b(a);
    auto it=b.begin();
    advance(it,6);
    b.insert(it,6,6);
    for(auto &i:b)
        cout<<i<<endl;
    cout<<cnt;
    return 0;
}

输出：

image.png

删除元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <vector>
#include <iostream>
using namespace std;
 
int main()
{
    vector<int>demo{ 1,2,3,4,5 };
    demo.pop_back();
    //输出 dmeo 容器新的size
    cout << "size is :" << demo.size() << endl;
    //输出 demo 容器新的容量
    cout << "capacity is :" << demo.capacity() << endl;
    for (int i = 0; i < demo.size(); i++) {
        cout << demo[i] << " ";
    }
    return 0;
}

输出：

1
2
3
size is :4
capacity is :5
1 2 3 4

可以看出，虽然最后一个元素被删去了，但是容器容量并没有变。

erase函数：

1
iterator erase (pos);

其中pos为迭代器，表示要删除元素的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <vector>
#include <iostream>
using namespace std;
 
int main()
{
    vector<int>demo{ 1,2,3,4,5 };
    auto iter = demo.erase(demo.begin() + 1);//删除元素 2
    //输出 dmeo 容器新的size
    cout << "size is :" << demo.size() << endl;
    //输出 demo 容器新的容量
    cout << "capacity is :" << demo.capacity() << endl;
    for (int i = 0; i < demo.size(); i++) {
        cout << demo[i] << " ";
    }
    //iter迭代器指向元素 3
    cout << endl << *iter << endl;
    return 0;
}

输出：

1
2
3
4
size is :4
capacity is :5
1 3 4 5
3

删除元素，容器的size变小了，但是容量并没有变，迭代器指向删除元素的下一个元素。

Map

#include<map>

STL的一个关联容器，有映射功能。

定义：

1
map<int,string> m;

第一个值为 键，第二个值为 值。

键相当于数组下标，值相当于数组里存储的东西。

使用：

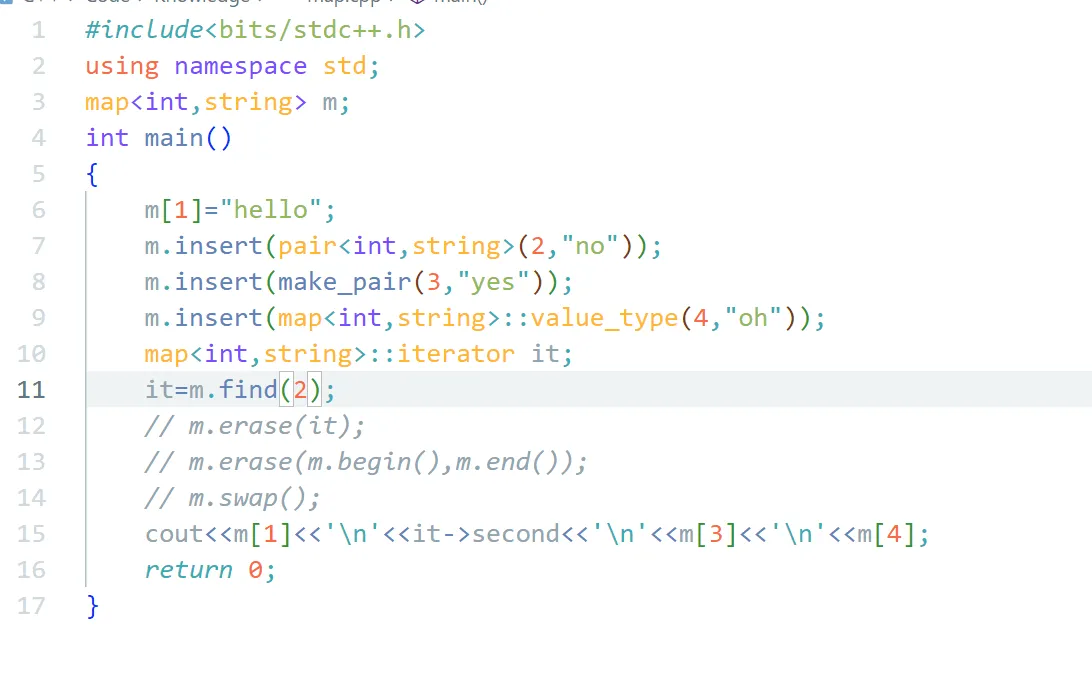
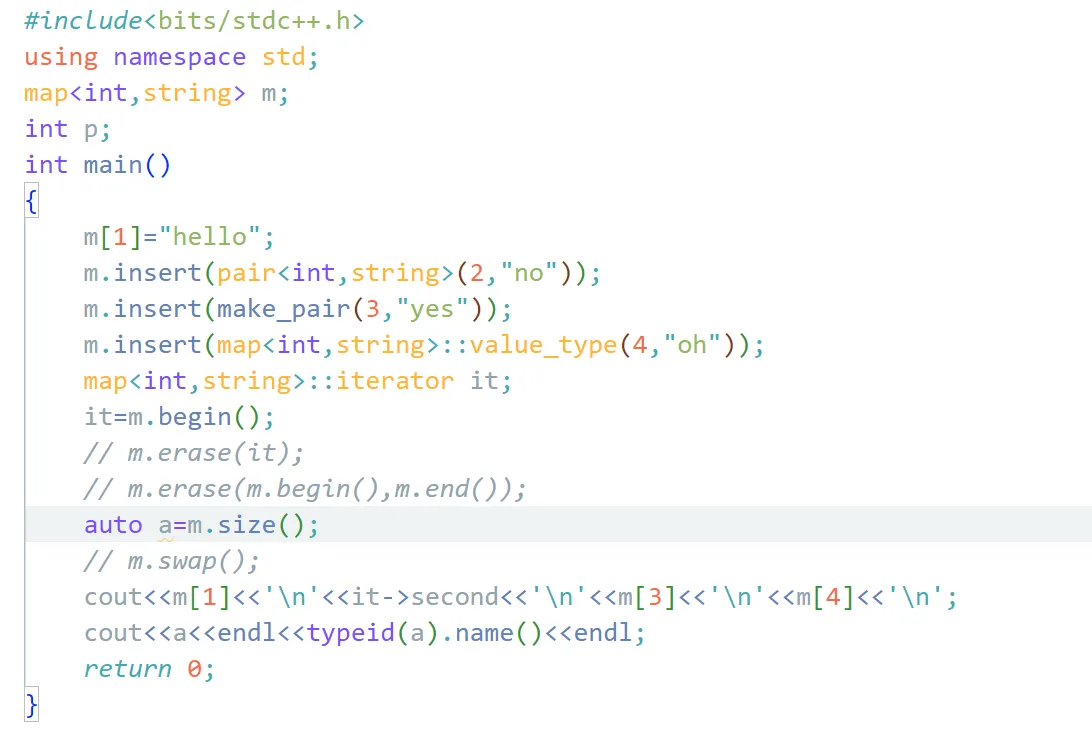
1
2
3
4
5
6
7
8
9
10
11
12
#include<bits/stdc++.h>
using namespace std;
map<int,string> m;
int main()
{
    m[1]="hello";
    m.insert(pair<int,string>(2,"no"));
    m.insert(make_pair(3,"yes"));
    m.insert(map<int,string>::value_type(4,"oh"));
    cout<<m[1]<<'\n'<<m[2]<<'\n'<<m[3]<<'\n'<<m[4];
    return 0;
}

这里提供了三种不同的插入元素方法。

当访问不存在的元素时，会返回空。

删除与清空：

1
2
3
map<int,string>::iterator it;
it=m.find(2);
m.erase(it);

或者

1
m.erase(2);

注意m.find()返回的是键的迭代器而非 值 的。

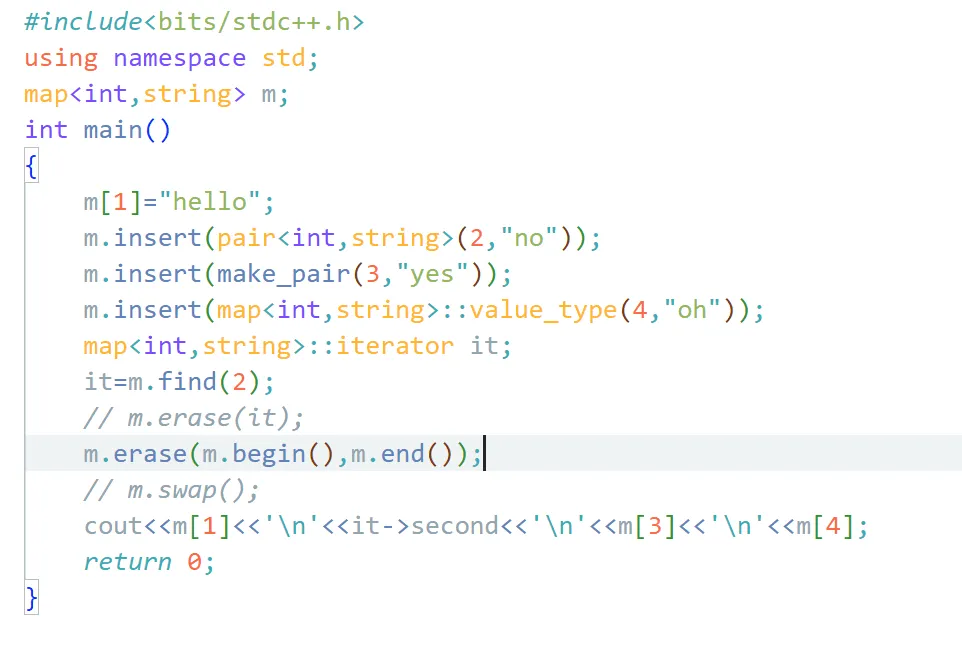
1
m.erase(m.begin(),m.end());

这里.begin()和.end()返回的也都是迭代器。

1.

这是这串代码正常的运行结果。

2.

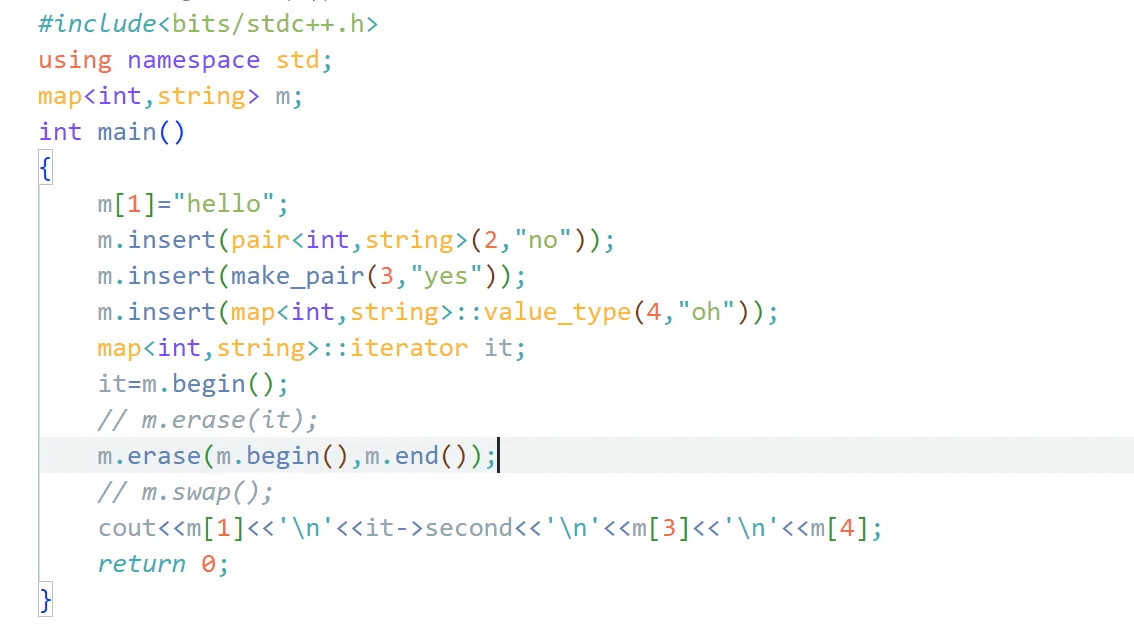
假如我先找到key=2key=2的元素的迭代器并储存，清空map后找到的迭代器依旧可以访问。

3.

但是如果是将m.begin()的迭代器存下来清空后却访问不到了。

大小

m.size()

image.png

image.png

m.size()虽然输出为整数，但是类型返回值却是y，这个类型我也不得而知，反正返回值不是一个整数，所以拿.size()和整型比较的时候一定要先把.size()赋值给一个整型，不然可能就会把负数变成较大的无符号值导致出错。

Unordered_map

map和unordered_map的差别和使用_map和unorderedmap的区别-CSDN博客

map 元素有有序性，但空间占用率高。

unordered_map 查询快，原理是哈希表。

Queue

Queue

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
int bj[2333];
queue<int> q;
int main()
{
    int m,n;
    scanf("%d%d",&m,&n);
    int cnt=0;
    while(n--)
    {
        int en;
        scanf("%d",&en);
        if(!bj[en])
        {
            ++cnt;
            q.push(en);
            bj[en]=1;
            while(q.size()>m)
            {
                bj[q.front()]=0;
                q.pop();
            }
        }
    }
    printf("%d\n",cnt);
    return 0;
}

List

STL

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
/*STL的List*/
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    list<int> node;
    for(int i=1;i<=n;i++)
        node.push_back(i);
    list<int>::iterator it=node.begin();
    while(node.size()>1)
    {
        for(int i=1;i<m;i++)
        {
            it++;
            if(it==node.end()) it=node.begin();
        }
        cout<<*it<<" ";
        list<int>::iterator next=++it;
        if(next==node.end()) next=node.begin();
        node.erase(--it);
        it=next;
    }
    cout<<*it;
    return 0;
}

Priority_queue

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<bits/stdc++.h>
using namespace std;
priority_queue<int,vector<int>,greater<int> > q;//小根堆定义<less>为从大到小，<greater>为从小到大
int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        int op;
        scanf("%d",&op);
        if(op==1)//入堆
        {
            int x;
            scanf("%d",&x);
            q.push(x);
        }
        else if(op==2)
        {
            printf("%d\n",q.top());
        }
        else q.pop();
    }
}
1
2
3
4
5
6
7
q.push()
q.pop()
q.size()
q.empty()
q.top()
q.top()
q.back()

Stack

例题TextReverse:

操作作用
st.push(i)将i元素放到栈顶
st.top()返回栈顶元素
st.pop()弹出栈顶元素
st.size()查询栈中元素
st.empty()查询栈是否为空
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    scanf("%d",&n);
    getchar();
    while(n--)
    {
        stack<char> s;
        while(1)
        {
            char ch=getchar();
            if(ch==' '||ch=='\n'||ch==EOF)
            {
                while(!s.empty()) printf("%c",s.top()),s.pop();
                if(ch=='\n'||ch==EOF) break;
                printf(" ");
            }
            else s.push(ch);
        }
        puts("");
    }
    return 0;
}

Bitset

  • size() 返回 std::bitset 的长度
  • count() 返回 std::bitset 中值为 1 的位的数量
  • any() 返回 std::bitset 中是否存在值为 1 的位
  • none() 返回 std::bitset 中是否所有位都是 0
  • all() 返回 std::bitset 中是否所有位都是 1
  • test(pos) 返回 std::bitset 中位于 pos 位置的值
  • set(pos) 将 std::bitset 中位于 pos 位置的值设为 1
  • reset(pos) 将 std::bitset 中位于 pos 位置的值设为 0
  • flip(pos) 将 std::bitset 中位于 pos 位置的值取反
  • to_ulong() 返回 std::bitset 转换成的无符号整数值
  • to_ullong() 返回 std::bitset 转换成的无符号长整数值
  • _Find_first() 返回第一个 1 的位置，若没有则返回 size
  • _Find_next() 返回下一个 1 的位置，若没有则返回 size

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<bits/stdc++.h>
using namespace std;
int main()
{
    bitset<4> a1;
    bitset<10> a2(15); // 二进制初始化
    string s = "10001001"; // 字符串初始化
    bitset<10> a3("10001001"); // 前面用0补位，或者bitset<10> a3(s);
    // 如果超出，则从后往前取，若长度不足，则前面用0补位
    cout << a3 << endl;
    cout << a2 << endl;
    a2 &= a3; // 必须长度相同才能进行位运算
    cout << a2 << endl;
    for(int i = 0; i <= 9; i++)
        cout << a2[i] << ' ';
    return 0;
}

Multiset

logn 的时间内保证序列中的数是有序的。

比较函数需要自己重载。

multiset

与 set 的最大差别就是它可以存储同一个数很多次（可重集）。

  • insert 插入
  • erase 删除
  • multiset<rec, cmp> h 定义排序方式

Set

维护一个集合，集合内的值都是有序的，那么理论上我们可以用它求第 k 小数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <bits/stdc++.h>
using namespace std;

int main()
{
    int k;
    cin >> k;
    set<int> s;
    s.insert(114514);
    s.insert(1919810);
    s.insert(12);
    s.insert(1);
    s.insert(5);
    set<int>::iterator it = s.begin();
    // advance(it, k);
    for(int i = 1; i <= k; i++) it++;
    cout << *it << endl;
    return 0;
}

二叉树

遍历

广度优先遍历(BFS)

没啥好说的。

深度优先遍历(DFS)

1.先序遍历

根-左-右

2.中序遍历

左-根-右

3.后序遍历

左-右-根

4.练习

HDU1710

此坑待填ing

不是很会

哈夫曼树

二叉树上两点间路径长度：这条路经过的边的数量。

树的路径长度：从根到每个节点的路径之和。

带权节点的带权路径长度：根节点到该点的路径长度乘以节点权值。

树的带权路径长度：所有叶子节点的带权路径长度之和。

现给定n个权值，构造一棵n个叶子节点的二叉树，每个叶子节点对应一个权值，那么带权路径最小的二叉树就叫做哈夫曼树。

要构造这样一颗树，那么肯定就是把权值大的叶子节点放在深度较小的地方，把权值小的叶子节点放在深度较大的地方。

算法流程：数据结构——哈夫曼树（Huffman Tree）

注：仅有叶子节点有权值。

哈夫曼编码其实就是构造出一颗哈夫曼树，以字符为权值，左儿子为0 右儿子为1。

习题：POJ1521

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// #include<bits/stdc++.h>//POJ不让用万能头aaa
#include<iostream>
#include<queue>
#include<string>
#include<cstdio>
#include<algorithm>
using namespace std;
int main()
{
    priority_queue< int,vector<int>,greater<int> > q;
    string s;
    while(getline(cin,s)&&s!="END")
    {
        sort(s.begin(),s.end());//字符串按字典序排序方法
        int num=1;
        int l=s.length();
        for(int i=1;i<=l;i++)//字符串从0开始，先比较0和1
        {
            if(s[i]!=s[i-1])
            {
                q.push(num);
                num=1;
            }
            else num++;
        }
        int ans=0;
        if(q.size()==1)//只有一个字符的字符串
        ans=s.length();
        while(q.size()>1)
        {
            int a=q.top();
            q.pop();
            int b=q.top();
            q.pop();
            q.push(a+b);
            ans+=a+b;
        }
        q.pop();
        printf("%d %d %.1f\n", 8*s.length() , ans , (double)8*s.length()/(double)ans);
    }
    return 0;
}

堆

手写堆

P3378

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int heap[N],len=0;
void push(int x)//小根堆插入
{
    heap[++len]=x;
    int i=len;
    while(i>1&&heap[i]<heap[i/2])//i/2为i的父元素下标
    {
        swap(heap[i],heap[i/2]);
        i=i/2;
    }
}
void pop()
{
    heap[1]=heap[len--];//将堆头替换为最后一个节点，开始下沉
    int i=1;
    while(2*i<=len)//2*i即为i的左儿子,循环终止条件是i没有儿子
    {
        int son=2*i;
        if(son<len&&heap[son+1]<heap[son])//右二子更小，那就让右儿子上浮
            son++;//切换为右儿子
        if(heap[son]<heap[i])//比当前要小，可以上浮
        {
            swap(heap[i],heap[son]);
            i=son;
        }
        else break;//不能继续下沉就终止
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        int op;
        scanf("%d",&op);
        if(op==1)//入堆
        {
            int x;
            scanf("%d",&x);
            push(x);
        }
        else if(op==2)
        {
            printf("%d\n",heap[1]);
        }
        else pop();
    }
    return 0;
}

练习

P2085

P2827

P3045

并查集

操作：

  • 合并两个集合
  • 查询某个元素的祖宗节点

优化：

  • 路径压缩（O(logn)O(logn)）
  • 按秩合并（O(logn)O(logn)）
  • 路径压缩+按秩合并（O(αn)≈O(1)O(\alpha n)\approx O(1)

扩展：

  • 记录每个集合的大小，一个集合大小是一定的，所以把它绑定到根节点身上就行。
  • 每个点到根节点的距离，绑定到每个元素身上。

AcWing1250

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <bits/stdc++.h>
using namespace std;
const int N = 40005;

int n, m;
int p[N];

int get(int x, int y)
{
    return x * n + y;
}
int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;
    for(int i = 0; i < n * n; ++i)
        p[i] = i;
    int res = 0;
    for(int i = 1; i <= m; ++i)
    {
        int x, y;
        char d;
        cin >> x >> y >> d;
        x--, y--;
        int a = get(x, y);
        int b;
        if(d == 'D') b = get(x + 1, y);
        else b = get(x, y + 1);
        int pa = find(a), pb = find(b);
        if(pa == pb)
        {
            res = i;
            break;
        }
        p[pa] = pb;
    }
    if(!res) puts("draw");
    else cout << res << endl;
    return 0;
}

AcWing1252

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>
using namespace std;
const int N = 10005;

int n, m, val;
int p[N];
int v[N], w[N];
int f[N];

int find(int x)
{
    if(x != p[x]) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m >> val;
    for(int i = 1; i <= n; ++i)
        cin >> v[i] >> w[i];
    for(int i = 1; i <= n; ++i)
        p[i] = i;
    for(int i = 1; i <= m; ++i)
    {
        int a, b;
        cin >> a >> b;
        int pa = find(a), pb = find(b);
        if(pa != pb)
        {
            v[pb] += v[pa];
            w[pb] += w[pa];
            p[pa] = p[pb];
        }
    }
    for(int i = 1; i <= n; ++i)
        if(p[i] == i)
            for(int j = val; j >= v[i]; --j)
                f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[val] << endl;
    return 0;
}

AcWing237

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <bits/stdc++.h>
using namespace std;
const int N = 2e6 + 8;
// 约束条件的顺序不影响矛盾：先考虑所有的相等，那么不会出现矛盾
// 然后再考虑不等条件，如果这个时候不满足，那么就出现了矛盾。

int n, m;
int p[N];
struct node
{
    int x, y, e;
}q[N];
unordered_map<int, int> S;

int get(int x)
{
    if(S.count(x) == 0) S[x] = ++n;
    return S[x];
}
int find(int x)
{
    if(x != p[x]) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        n = 0;
        S.clear();
        scanf("%d", &m);
        for(int i = 0; i < m; i++)
        {
            int x, y, e;
            scanf("%d%d%d", &x, &y, &e);
            q[i] = {get(x), get(y), e};
        }
        for(int i = 1; i <= n; ++i) p[i] = i;
        for(int i = 0; i < m; ++i)
            if(q[i].e == 1)
            {
                int pa = find(q[i].x), pb = find(q[i].y);
                p[pa] = pb;
            }
        bool bj = false;
        for(int i = 0; i < m; ++i)
            if(q[i].e == 0)
            {
                int pa = find(q[i].x), pb = find(q[i].y);
                if(pa == pb)
                {
                    bj = true;
                    break;
                }
            }
        if(bj) printf("NO\n");
        else printf("YES\n");
    }
    return 0;
}

AcWing238

维护间隔多少战舰。

维护一下每个节点到根节点的距离即可。

让排头当根节点。

同时还要维护一下 sizesize

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;
const int N = 3e4 + 8;

int m;
int s[N];
int d[N];
int p[N];

int find(int x)
{
    if(x != p[x])
    {
        int root = find(p[x]);
        d[x] += d[p[x]];
        p[x] = root;
    }
    return p[x];
}

int main()
{
    cin >> m;
    for(int i = 1; i <= 3e4; i++) 
    {
        p[i] = i;
        s[i] = 1;
    }
    while(m--)
    {
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);
        if(op[0] == 'M')
        {
            int pa = find(a), pb = find(b);
            if(pa != pb)
            {
                d[pa] = s[pb];
                s[pb] += s[pa];
                p[pa] = pb;
            }
        }
        else
        {
            int pa = find(a), pb = find(b);
            if(pa != pb) printf("-1\n");
            else printf("%d\n", max(0, abs(d[a] - d[b]) - 1));
        }
    }
    return 0;
}

AcWing239

类似食物链。

带权并查集维护的是它与根节点之间的关系。

同类/不同类

image.png

小结论：模二意义下的加法相当于异或。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 20005;

int n, m;
int p[N];
int d[N];
unordered_map<int, int> S;

int get(int x)
{
    if(S.count(x) == 0) S[x] = ++n;
    return S[x];
}
int find(int x)
{
    if(p[x] != x)
    {
        int root = find(p[x]);
        d[x] ^= d[p[x]];
        p[x] = root;
    }
    return p[x];
}

int main()
{
    cin >> n >> m;
    n = 0;
    int res = m;
    for(int i = 1; i < N; i++) p[i] = i;
    for(int i = 1; i <= m; i++)
    {
        int a, b;
        string type;
        cin >> a >> b >> type;
        a = get(a - 1), b = get(b); // 前缀和思路
        int t = 0;
        if(type == "odd") t = 1; //奇数,a 和 b 不是同类
        int pa = find(a), pb = find(b);
        if(pa == pb)
        {
            if((d[a] ^ d[b]) != t) // 不是同类的话和根节点的关系就应该不同，否则矛盾
            {
                res = i - 1;
                break;
            }
        }
        else
        {
            p[pa] = pb;
            d[pa] = d[a] ^ d[b] ^ t; // 同类异或为0，异类异或为1，分类讨论即可
        }
    }
    cout << res << endl;
    return 0;
}

线段树

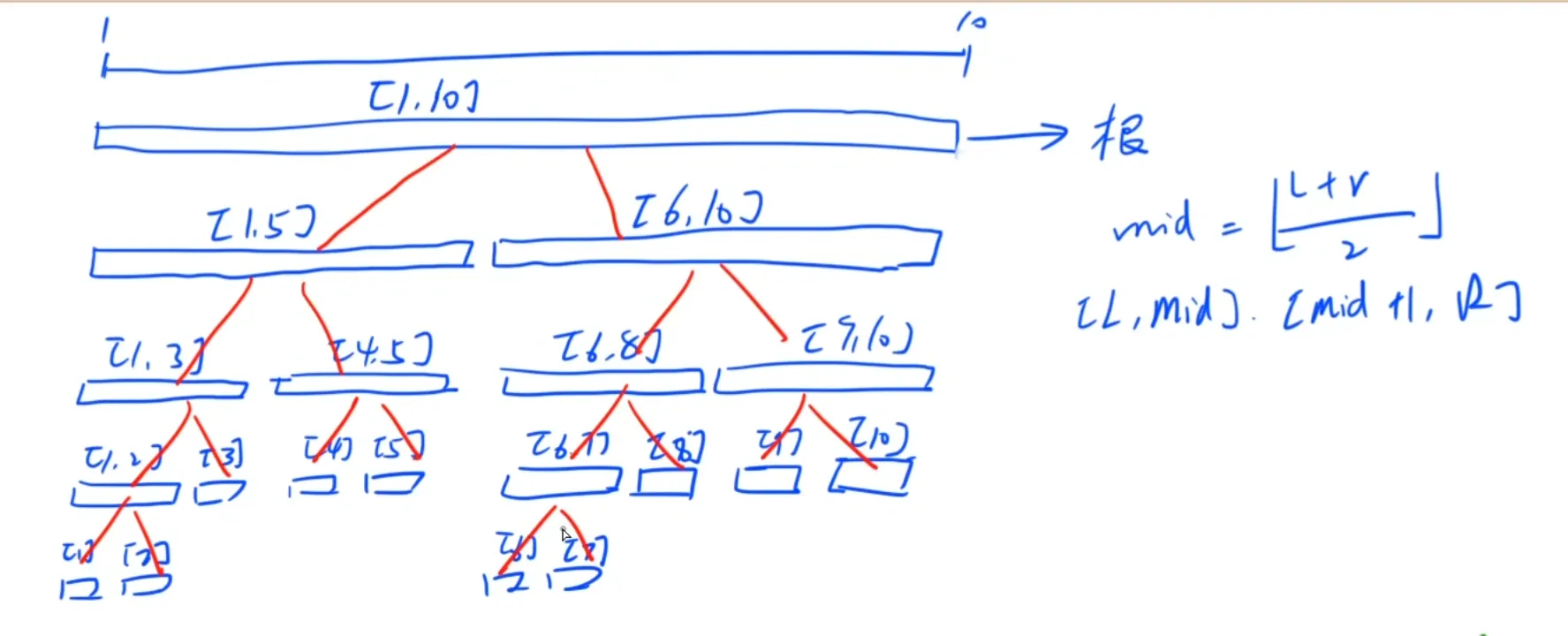
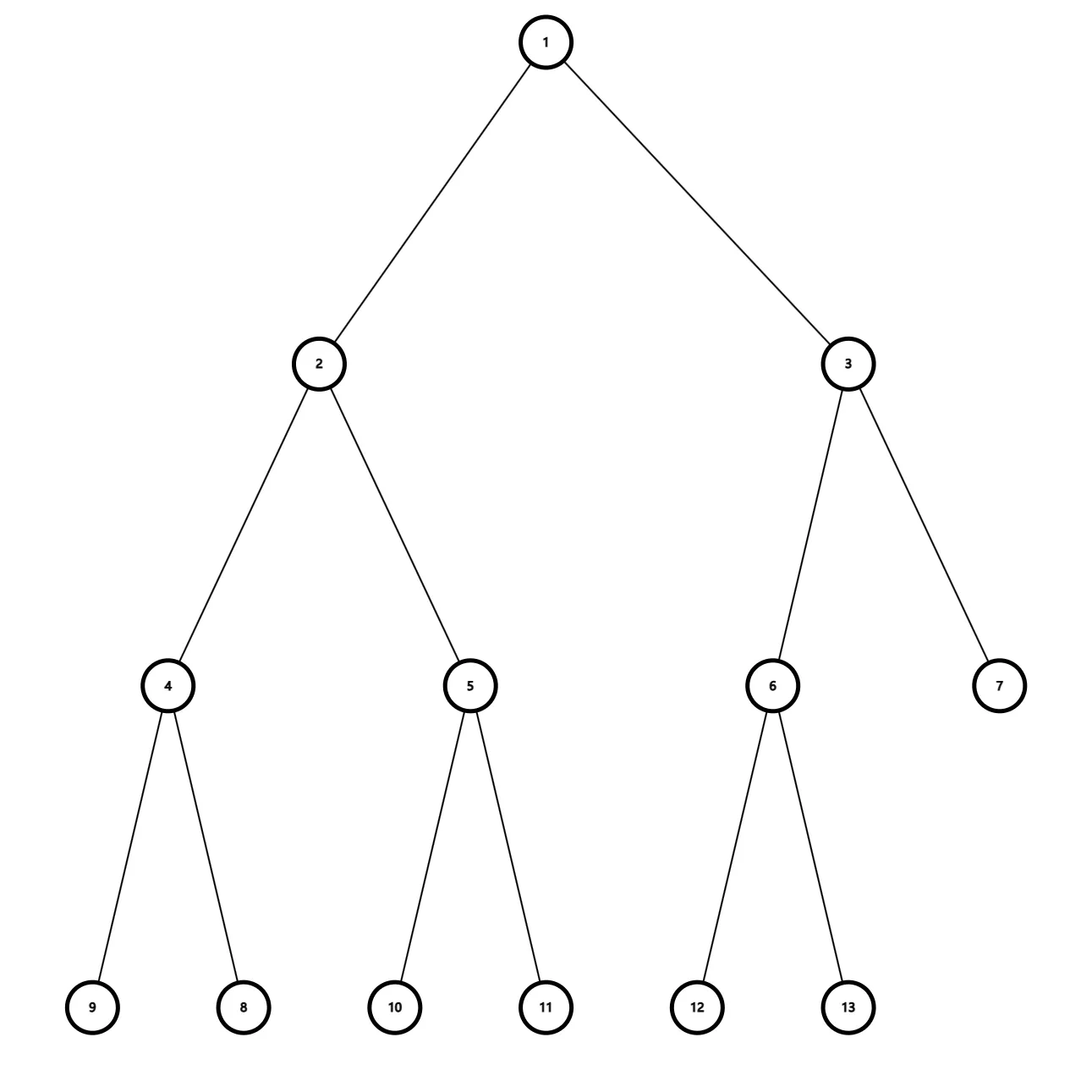
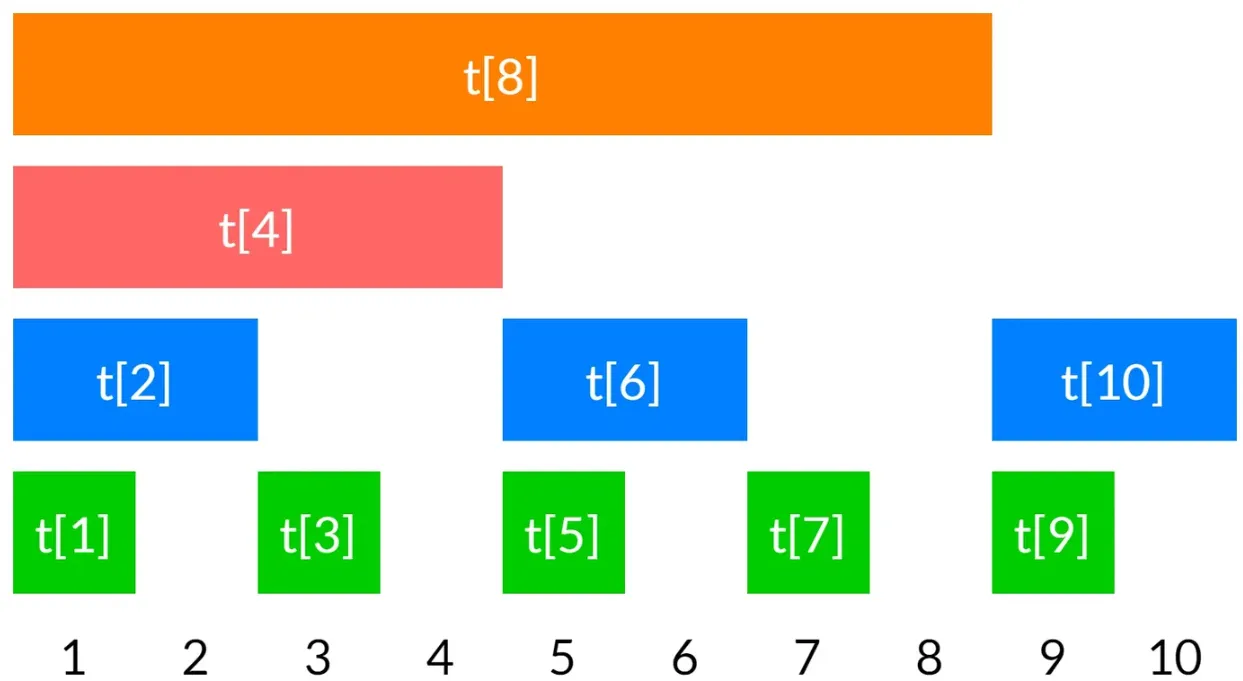
顾名思义，就是以区间为节点的二叉树

这是它的样子：

image.png

和堆一样，线段树也是用一维数组存储。

（8 9 反了）

  • 父节点：⌊x2⌋\lfloor{\dfrac{x}{2}}\rfloor
  • 左儿子：2x2x，x<<1
  • 右儿子：2x+12x+1，x<<1|1

长度为 nn 的一段区间：

叶子节点数为 nn 个

倒数第二层最多为 nn 个节点，

二叉树性质：

  • 区间长度和叶子节点数相同
  • 深度为k−1k-1的满二叉树有2k−1−12^{k-1}-1个节点，第kk层有2k−12^{k-1}个节点，那么第k−1k-1层有2k−1−12^{k-1-1}个节点，也就是2k−22^{k-2}个节点，那么第k−1k-1层往上共有2k−2−12^{k-2}-1个节点。
  • 第ii层（不是最后一层）的节点数是第ii层以上的节点数-1。

所以倒数第二层以上的节点数最多为n−1n-1个，那么除了最后一层的节点数最多为2n−12n-1个。

最后一层不断往上加，最多可以加满为2n2n个，所以总节点数最大为4n−14n-1，所以线段树的空间要开四倍。

另一种讲法：

一棵线段树区间长度为 nn，假设有 kk 层，n=2kn=2^k，即满二叉树。

那么此时总节点数为：2n−12n-1，不懂的可以回顾一下二叉树相关知识点。

那假如区间长度加一，变成了 n+1n+1，那么这多出来的一个节点在 k+1k+1 层，第 k+1k+1 层的 indexindex 范围为 [2n,4n−1][2n, 4n-1]，多出来的这个节点编号可能是其中的任何一个，所以保险起见，开 4n4n 的空间是绝对够的。

建树

1
2
3
4
void pushup(int u)//由子节点信息更新父节点信息（最大值）
{
    tr[u].v=max(tr[u<<1].v,tr[u<<1|1].v);
}
1
2
3
4
5
6
7
8
9
void build(int u,int l,int r)
{
    tr[u]={l,r,0};
    if(l==r) return;
    int mid=(l+r)>>1;
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
    pushup(u);
}

查询

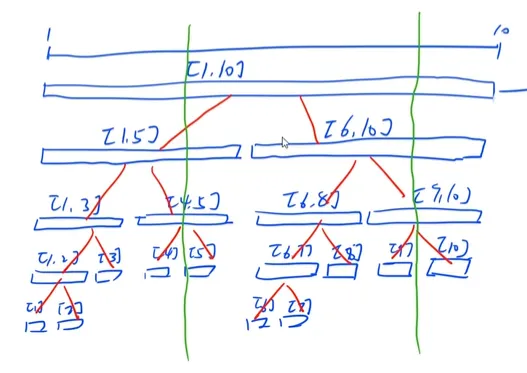
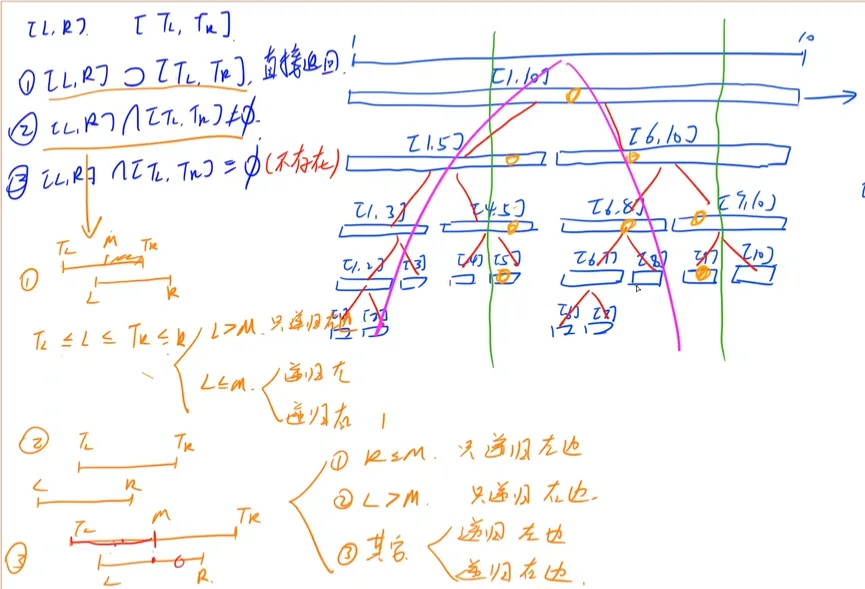
比如查询某段区间的最大值。

image.png

查询的过程中无非就两种情况：查询区间与当前所在区间是包含关系还是交叉关系。

如果是包含关系，即查询区间包含树上区间，那么就没必要往下递归了，直接返回该段最大值即可。比如图中右分支递归到[6,10][6,10]，然后递归到[6,8][6,8]和[9,10][9,10]，这时候我们发现其实[6,8][6,8]没有向下递归的必要了，只需要直接返回该段区间的最大值即可。

如果是交叉关系，那么就接着向下递归，例如[9,10][9,10]区间再接着往下递归，在这个过程中若访问区间与查询区间没有交集，那么就不用管了，就不用访问它。

访问到的区间数量是loglog级别的。

image.png

由于奇数除以22的时候是下取整，所以只要包含midmid那么就要访问左区间。

最多大概会有4logn4logn的访问。

1
2
3
4
5
6
7
8
9
int query(int u,int l,int r)
{
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].v;//树中线段被查询区间包含
    int mid=(tr[u].l+tr[u].r)>>1;
    int v=0;
    if(l<=mid) v=query(u<<1,l,r);
    if(r>mid) v=max(v,query(u<<1|1,l,r));
    return v;
}

单点修改

从上往下递归，直到递归到某个叶子节点。

然后对它进行pushup就可以了。

pushup其实就是从底下往上重新算一遍每个区间的和就可以了。

1
2
3
4
5
6
7
8
9
10
11
void modify(int u,int x,int v)//修改
{
    if(tr[u].l==x&&tr[u].r==x) tr[u].v=v;
    else
    {
        int mid=(tr[u].l+tr[u].r)>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);//更新
    }
}

懒标记

区间加法

比如区间修改加访问区间和。

如果没有懒标记，那么只需要记录当前区间的总和。

现在还需要再加上懒标记add。

add含义是以当前节点为根节点的子树中的每个节点都加上add这个数。

包不包含自己都可以，保证前后一致即可，下面采用只给子树加。

这样修改的复杂度就只有O(logn)O(logn)了。

访问时需要把祖宗节点的值累计到子孙上。

只要在递归的时候清空当前懒标记并且将懒标记传给儿子，其实就是pushdown。

pushdown

这种是当前区间更新标记，而子树节点信息不更新的写法。

1
2
3
4
l.add+=root.add;
l.sum+=(l.r-l.l+1)*root.add;
r.add+=root.add;
r.sum+=(r.r-r.l+1)*root.add;

修改的时候就往下传。

类似于查询，当递归到包含了这个节点，那么就没必要接着往下递归，打上标记然后返回就可以了。

递归到子区间需要把当前区间的标记下传并清空自身标记。

相当于查询和修改追着下放跑，总之我对当前节点做操作的时候，这个节点必须是没有标记的。

假如修改区间的左端点≤mid\le{mid}，那么就要递归修改左区间；

假如修改区间的右端点>mid>{mid}，那么就要递归修改右区间。

补充说明：

对于下传更好的理解：

假如你是个很懒惰的工人，有很多工作都推着不做，但是某天老板带着一堆人来查工，很幸运的是他们参观的都很慢，所以你就紧急地处理他们将要到达的地方，以保证他们查到这个地方的时候发现你已经把这个地方的工作做完了，你永远比老板快一步，你永远都是对的，至于他们不查的地方，你自然也懒得去做，也就是所谓“懒标记”。

所以为什么每次要修改儿子和查询儿子之前要先下传？

因为老板要去儿子节点的地方查工了。

区间乘法

再加一个懒标记mul，表示乘法的懒标记。

假如先加再乘处理标记，那假如再加了一个数，变成了(s+a)×b+c(s+a)\times{b}+c的形式，会非常不好处理，因为如果想把 cc 加到 aa 上，需要除以一个 bb，会造成精度误差。

那就先乘再加，如果什么都没有那么mul=1,add=0mul=1,add=0，这样就比较好维护。

对于每个数，x×mul+addx\times{mul}+add，假如再加一个数，那么只需要改变addadd就可以了。

而对于乘法，那就把addadd和mulmul同时乘上这个数就可以了。

扫描线法

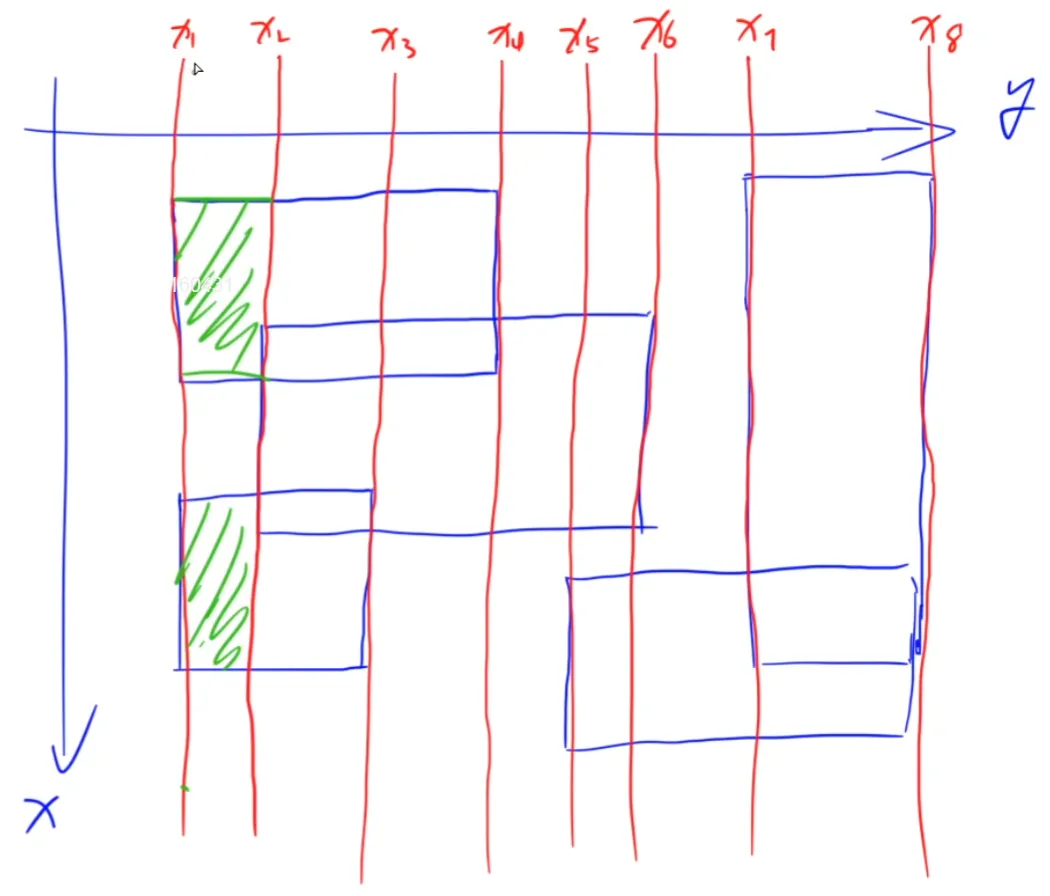
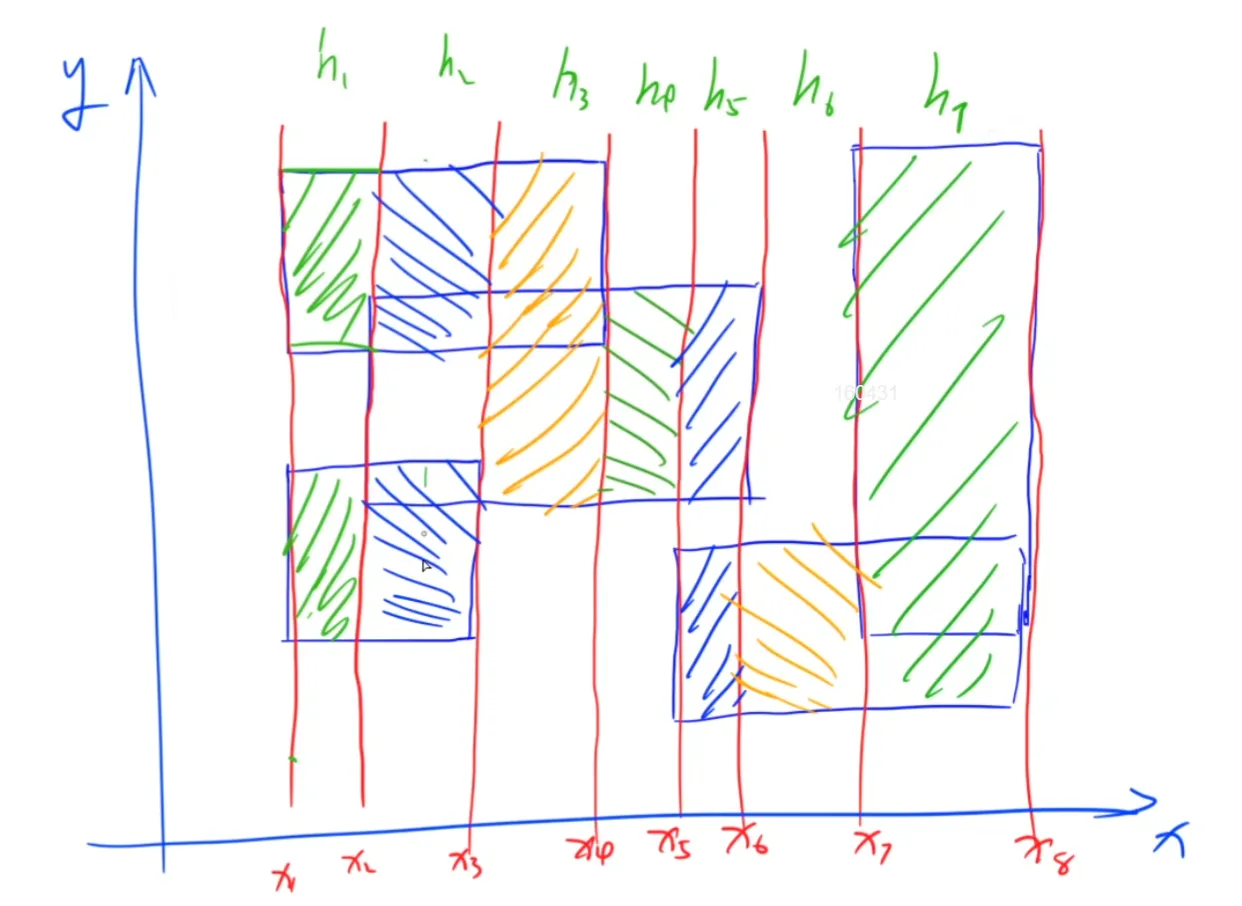
image.png

像这样沿着矩形的侧边切若干刀，将整个图形分成若干份，使得每一份内的截线长度都相等。

image.png

hih_i代表第ii段面积的长度。

那怎么求出hih_i呢？

可以对纵坐标进行线段树维护。

每个矩形有两条侧边，把每个侧边看成一个线段，权值分别设为+1,−1+1,-1，表示当前区间被几个矩形所覆盖。

有两个操作，一个是将某个区间加一或负一，一个是求整个区间里权值大于00的区间长度是多少。

维护的是区间，修改 l∼rl\sim{r} 只需要修改 yl∼yr−1y_l\sim{y_{r-1}}

统计信息时只关心子孙节点。

扫描线性质：

  • 永远只考虑根节点信息，查询的时候不需要下放标记。
  • 所有操作都是成对出现，有加也就有减。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n;
struct segment
{
    double x,y1,y2;
    int k;
    bool operator<(const segment &a)const
    {
        return x<a.x;
    }
}seg[N<<1];
struct node
{
    int l,r;
    int cnt;
    double len;
}tr[N<<3];
vector<double> ys; 
int find(double y)//查找离散化后的下标
{
    return lower_bound(ys.begin(),ys.end(),y)-ys.begin();
}
void pushup(int u)
{
    if(tr[u].cnt)
        tr[u].len=(ys[tr[u].r+1]-ys[tr[u].l]);//节点对应区间，所以右端点下标要加一
    else if(tr[u].l!=tr[u].r)//不是叶子节点再用儿子更新
        tr[u].len=tr[u<<1].len+tr[u<<1|1].len;
    else tr[u].len=0;
}
void build(int u,int l,int r)
{
    tr[u].l=l,tr[u].r=r;
    if(l==r)
    {
        tr[u].len=0,tr[u].cnt=0;
        return;
    }
    int mid=(l+r)>>1;
    build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}
void modify(int u,int l,int r,int v)
{
    if(tr[u].l>=l&&tr[u].r<=r) 
    {
        tr[u].cnt+=v;
        pushup(u);//算一下要不要更新
        return;
    }
    int mid=(tr[u].l+tr[u].r)>>1;
    if(l<=mid) modify(u<<1,l,r,v);
    if(r>mid) modify(u<<1|1,l,r,v);
    pushup(u);
}
int main()
{
    int t=1;
    while(scanf("%d",&n),n)
    {
        ys.clear();
        for(int i=1,j=0;i<=n;i++)
        {
            double x1,x2,y1,y2;
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            seg[j++]={x1,y1,y2,1};
            seg[j++]={x2,y1,y2,-1};
            ys.push_back(y1),ys.push_back(y2);
        }
        sort(ys.begin(),ys.end());
        ys.erase(unique(ys.begin(),ys.end()),ys.end());
        sort(seg,seg+n*2);
        build(1,0,(int)ys.size()-2);//存的是区间
        double res=0;
        for(int i=0;i<n*2;i++)
        {
            if(i>0) res+=tr[1].len*(seg[i].x-seg[i-1].x);
            modify(1,find(seg[i].y1),find(seg[i].y2)-1,seg[i].k);//因为存的是区间而不是点，所以右端点要减一，因为一号节点代表的是1~2，那么l~r对应的节点就是l~r-1
        }
        printf("Test case #%d\n",t++);
        printf("Total explored area: %.2lf\n\n",res);
    }
    return 0;
}

动态开点

线段树的堆式存储：

总共有 nn 个数，lognlogn 层，最后一层叶子节点数是 2⌈logn⌉2^{\lceil{logn}\rceil}，由于万全二叉树的性质，总节点数就是 2⌈logn⌉+1−12^{\lceil{logn}\rceil + 1} - 1，最后一层的叶子节点最多有 nn 个，那么总节点数最多有 2n−12n - 1 个，这是正常情况。

在一些特殊情况下，倒数第二层最多有 n−1n - 1 个叶子节点，有一个节点在最后一层，那么倒数第二层及之前最多有 2n−32n - 3 个节点，而最后一层由于有了一个点所以要把这一层开满，也就是倒数第二层的两倍 2n−22n - 2，所以节点总数最多为 4n−54n - 5。

为了避免这种情况，所以我们物尽其用，做到用多少开多少，那么此时最大空间为 2n−12n - 1。

也就是要开两倍空间。

由于我们不再记录节点的左右边界，所以要放到函数参数里，pushdown 的时候也要记录一下节点区间大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 7;
typedef long long LL;
#define ls(x) tr[tr[x].l]
#define rs(x) tr[tr[x].r]

int n, m, idx, root;
int a[N];
struct Node
{
    int l, r;
    LL sum, add;
}tr[N << 1];

void pushup(int u)
{
    tr[u].sum = ls(u).sum + rs(u).sum;
}
void pushdown(int u, int len)
{
    if(tr[u].add)
    {
        if(!tr[u].l) tr[u].l = ++idx;
        if(!tr[u].r) tr[u].r = ++idx;
        ls(u).add += tr[u].add;
        rs(u).add += tr[u].add;
        ls(u).sum += (LL)(len + 1) / 2 * tr[u].add;
        rs(u).sum += (LL)len / 2 * tr[u].add;
        tr[u].add = 0;
    }
}
void modify(int &u, int l, int r, int L, int R, int v) // 节点编号，节点区间，修改区间，加v
{
    if(!u) u = ++idx;
    if(L <= l && r <= R)
    {
        if(l == r)
        {
            tr[u].sum += v;
            return;
        }
        tr[u].add += v;
        tr[u].sum += (LL)(r - l + 1) * v;
        return;
    }
    pushdown(u, r - l + 1);
    int mid = (l + r) >> 1;
    if(L <= mid) modify(tr[u].l, l, mid, L, R, v);
    if(R > mid) modify(tr[u].r, mid + 1, r, L, R, v);
    pushup(u);
}
LL query(int u, int l, int r, int L, int R)
{
    if(!u) return 0;
    if(L <= l && r <= R) return tr[u].sum;
    pushdown(u, r - l + 1);
    int mid = (l + r) >> 1;
    LL res = 0;
    if(L <= mid) res += query(tr[u].l, l, mid, L, R);
    if(R > mid) res += query(tr[u].r, mid + 1, r, L, R);
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        modify(root, 1, n, i, i, a[i]);
    }
    while(m--)
    {
        int op, x, y;
        scanf("%d%d%d", &op, &x, &y);
        if(op == 1)
        {
            int k;
            scanf("%d", &k);
            modify(root, 1, n, x, y, k);
        }
        else if(op == 2)
        {
            printf("%lld\n", query(root, 1, n, x, y));
        }
    }
    return 0;
}

可持久化线段树

又叫做主席树

MM 次修改， M+1M + 1 个版本。

某一个节点发生了变化，那就创建一个新的节点，否则就用原来的。

每次最多修改 4logn4logn 的点，所以一共需要最多 4logn×m4 logn \times m 倍的空间。

节点存储它的左右儿子的编号，节点的区间作为函数参数即可。

可持久化线段树难以进行区间修改。

因为有很多版本的很多懒标记需要更新。

除非做成永久化懒标记。

咕咕咕

相对于 Trie 树，它不会新加入一些点。

只是把要修改的点复制过来，然后修改它的一部分信息。

相当于动态开点。

每次先开一个点，然后把之前版本相应的节点先复制过来，如果没有那么就相当于复制了空信息，

AcWing255

首先这是一个静态问题。

  • 归并树
  • 划分树
  • 树套树（线段树套平衡树）
  • 可持久化线段树
数据结构时间复杂度空间复杂度
划分树O(NlogN)O(NlogN)O(NlogN)O(NlogN)
树套树O(Mlog2N)O(Mlog^2N)O(NlogN)O(NlogN)
主席树O(NlogN)O(NlogN)O(NlogN)O(NlogN)

所以划分树被完全取代了。

用线段树维护值域。

这里插入一个概念：权值线段树。

以值域为下标建立线段树，维护的是一段值域内数的个数，相当于用线段树维护了一堆桶。

先将值域离散化。

在数值上建立线段树。

维护每个数值区间中一共有多少个数。

先考虑如何求整体第 kk 小数，可以进行二分，直到找到一个位置使得它左边小于等于 kk 的数刚好为 kk 。

对于右边界，可以查询历史版本。

每个版本相当于比原来的版本多加了一个数，改变了线段树中的 logNlogN 个节点。

而线段树每个版本的结构都是不变的。

总节点数量在变？那是因为有新版本的节点替代了老版本的节点，所以一开始空树里有 4N4N 个节点，后来还要再插入 NN 个数，每插入一个数最多可以增加 logNlogN 个节点，所以需要开的空间是 (4+logN)N(4 + logN)N 。

可以考虑前缀和，同时查一下 l−1l - 1 版本即可，这样就可以知道 l∼rl\sim r 的这些数内，某段值域的变化量，然后就可以类似二分地找到这些数中第 kk 小的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>
using namespace std;
const int N = 200010;

int n, m;
int a[N];
vector<int> nums;
struct Node 
{
    int l, r;
    int cnt;
}tr[(N << 2) + N * 17]; // 4N + NlogN
int root[N], idx;

int find(int x)
{
    return lower_bound(nums.begin(), nums.end(), x) - nums.begin(); // 离散化
}
int build(int l, int r) // 建立左右边界为 l 和 r 的线段树节点并返回其编号
{
    int p = ++idx;
    tr[p].l = l, tr[p].r = r;
    if(l == r) return p;
    int mid = (l + r) >> 1;
    tr[p].l = build(l, mid);
    tr[p].r = build(mid + 1, r);
    return p;
}
int insert(int p, int l, int r, int x) // 上一个版本的节点，左边界右边界，需要插入的数
{
    int q = ++idx; // 新节点
    tr[q] = tr[p]; // 先复制，注意由于树的结构没有发生改变，所以 p 和 q 分别对应着老版本和新版本中同一个节点。
    if(l == r)
    {
        tr[q].cnt++;
        return q;
    }
    int mid = (l + r) >> 1;
    if(x <= mid) tr[q].l = insert(tr[p].l, l, mid, x); // 注意第一个参数，历史版本同步递归
    else tr[q].r = insert(tr[p].r, mid + 1, r, x);
    tr[q].cnt = tr[tr[q].l].cnt + tr[tr[q].r].cnt; // 更新节点信息
    return q;
}
int query(int q, int p, int l, int r, int k) // 新版本，旧版本，左右边界，第 k 小的下标
{
    if(l == r) return r;
    int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt;
    int mid = (l + r) >> 1;
    if(k <= cnt) return query(tr[q].l, tr[p].l, l, mid, k);
    else return query(tr[q].r, tr[p].r, mid + 1, r, k - cnt);
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        nums.push_back(a[i]);
    }
    sort(nums.begin(), nums.end());
    nums.erase(unique(nums.begin(), nums.end()), nums.end());
    root[0] = build(0, nums.size() - 1); // 初始化空树
    for(int i = 1; i <= n; i++)
        root[i] = insert(root[i - 1], 0, nums.size() - 1, find(a[i]));
    while(m--)
    {
        int l, r, k;
        scanf("%d%d%d", &l, &r, &k);
        printf("%d\n", nums[query(root[r], root[l - 1], 0, nums.size() - 1, k)]);
    }
    return 0;
}

习题

A1275

A245

A247

A1277

image.png

树状数组

树形结构的数组

image.png

Lowbit函数

lowbit(i)=i&-i

这是树状数组最重要的一个环节。

单点修改向上传递时，每次加上当前点的lowbitlowbit

区间查询向下访问时，每次减去当前点的lowbitlowbit

习题

P3374

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define lowbit(x) ((x)&(-x))
const int N=5e5+7;
int n,m;
int a;
int t[N];
void modify(int x,int y)
{
    for(int i=x;i<=n;i+=lowbit(i))
        t[i]+=y;
}
ll query(int x,int y)
{
    ll ans=0;
    for(int i=y;i;i-=lowbit(i))
        ans+=t[i];
    for(int i=x-1;i;i-=lowbit(i))
        ans-=t[i];
    return ans;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a),modify(i,a);
    while(m--)
    {
        int op,x,y;
        scanf("%d%d%d",&op,&x,&y);
        if(op==1)
        {
            modify(x,y);
        }
        else
        {
            printf("%lld\n",query(x,y));
        }
    }
    return 0;
}

P3368

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
const int N=5e5+7;
int n,m,a;
int t[N];
void modify(int x,int y,int k)
{
    for(int i=x;i<=n;i+=lowbit(i))
        t[i]+=k;
    for(int i=y+1;i<=n;i+=lowbit(i))
        t[i]-=k;
}
ll query(int x)
{
    ll ans=0;
    for(int i=x;i;i-=lowbit(i))
        ans+=t[i];
    return ans;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a),modify(i,i,a);
    while(m--)
    {
        int op,x,y,k;
        scanf("%d%d",&op,&x);
        if(op==1)
        {
            scanf("%d%d",&y,&k);
            modify(x,y,k);
        }
        else
        {
            printf("%lld\n",query(x));
        }
    }
    return 0;
}

HDU1166

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-x))
const int N=5e4+10;
using namespace std;
int t[N];
int n;
inline void modify(int x,int y)
{
    for(int i=x;i<=n;i+=lowbit(i))
        t[i]+=y;
}
inline int query(int x,int y)
{
    int an=0;
    for(int i=y;i;i-=lowbit(i))
        an+=t[i];
    for(int i=x-1;i;i-=lowbit(i))
        an-=t[i];
    return an;
}
int main()
{
    int tt;
    scanf("%d",&tt);
    for(int i=1;i<=tt;i++)
    {
        scanf("%d",&n);
        memset(t,0,sizeof(t));
        for(int j=1;j<=n;j++)
        {
            int a;
            scanf("%d",&a);
            modify(j,a);
        }
        int x,y,ans;
        char ss[10];
        printf("Case %d:\n",i);
        while(scanf("%s",ss),ss[0]!='E')
        {
            if(ss[0]=='Q')
            {
                scanf("%d%d",&x,&y);
                ans=query(x,y);
                printf("%d\n",ans);
            }
            else if(ss[0]=='A')
            {
                scanf("%d%d",&x,&y);
                modify(x,y);
            }
            else if(ss[0]=='S')
            {
                scanf("%d%d",&x,&y);
                modify(x,-y);
            }
        }
    }
    return 0;
}

平衡树

Treap

Tree + heap

二叉搜索树和堆的一个有机结合。

BST

Binary search tree | 二叉搜索树

每个节点都有一个权值，满足当前节点的左子树中的任何一个点的权值，右子树的任何一个点的权值大于该点，若有重复的，那就记录一下这个值出现了多少次。

BST 的中序遍历是严格单调递增的。

它在动态维护一个有序序列。

  1. 插入
  2. 删除（叶节点）
  3. 找前驱（中序遍历的前一个位置）/后继（中序遍历的后一个位置）
  4. 找最大（不断走右儿子直到不能走）/最小值（不断走左儿子直到不能走）
    以上 set 均可满足
  5. 求某个值的排名
  6. 求排名是 k 的数是哪个
  7. 找到比某个数小的最大值
  8. 找到比某个数大的最小值

Treap 可以让 BST 尽量随机，使得其期望高度为 logn

节点：

1
2
3
4
5
struct node
{
	int l, r;
	int key, val; // 排序
}

key 代表 BST 中排序的关键字，而 val 为大根堆中排序的关键字，那么假如所有节点的这两个值都互不相同，那么可以确定出唯一的平衡树：从上往下递归，每层将子树节点分为两部分，左子树 key 都小于根节点，右子树 key 都大于根节点，然后分别取两部分的 val 的最大值的节点作为子树的根。

val 是一个随机值。

一般初始化可以为空，但为了防止越界，可以安排两个哨兵，一个为负无穷作为根节点，一个为正无穷作为根的右子树的根节点，那么就可以保证从右儿子的左子树中搜索一定是在边界范围内的。

平衡树一个点只会对应一个数，所以空间复杂度为 O(n)O(n)。

插入

递归插入，并给这个节点赋值一个 val，然后类似堆更新一下结构。

旋转

  • 右旋（zig）：

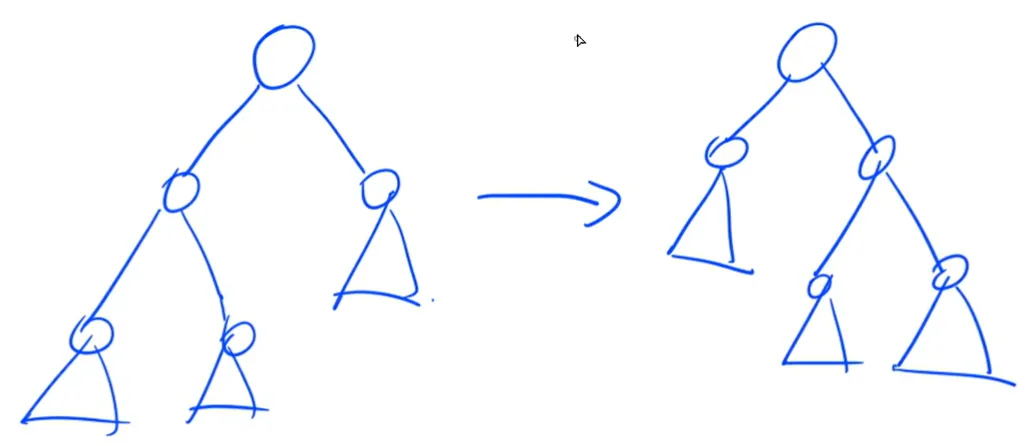
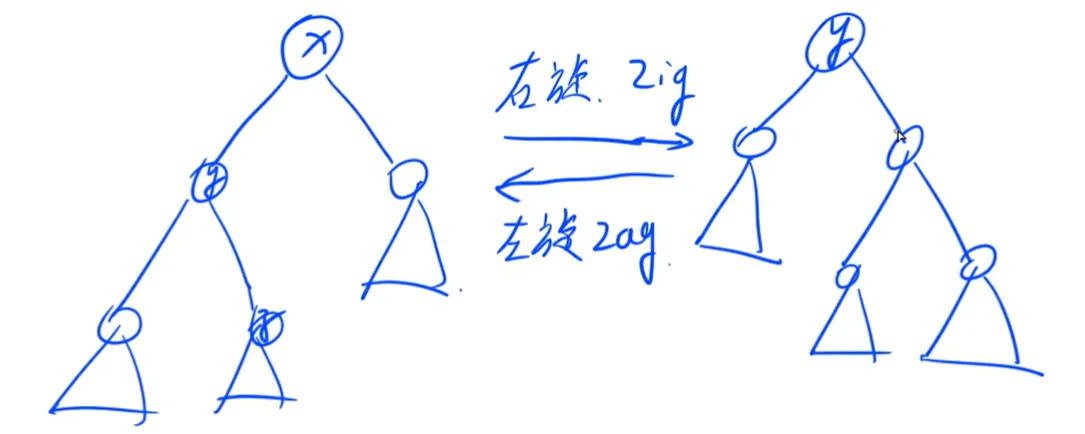
image.png

  • 左旋（zag）：

image.png

平衡树的旋转：右旋拎左右挂左，左旋拎右左挂右。

性质：

旋转完后不会改变平衡树的中序遍历。

左旋是交换一下一个节点和它右儿子的父子关系，也就是相当于把右儿子给左旋到了父亲的位置，同时要维护中序不变。

右旋同理。

旋转需要特判，哪个大旋转哪个上去。

AcWing235

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 7;
const int INF = 1e8;

int n;
struct Node
{
    int l, r;
    int key, val;
    int cnt, siz; // 这个数有几个，siz表示子树大小
}tr[N];

int root, idx;

int get_node(int key) // 创建节点
{
    tr[++idx].key = key;
    tr[idx].val = rand();
    tr[idx].cnt = tr[idx].siz = 1;
    return idx;
}
void pushup(int p)
{
    tr[p].siz = tr[tr[p].l].siz + tr[tr[p].r].siz + tr[p].cnt;
}
void build()
{
    get_node(-INF), get_node(INF);
    root = 1, tr[1].r = 2;
    pushup(root);
}
void zig(int &p) // 右旋
{
    int q = tr[p].l;
    tr[p].l = tr[q].r;
    tr[q].r = p;
    p = q; // 交换编号
    pushup(tr[p].r);
    pushup(p);
}
void zag(int &p)
{
    int q = tr[p].r;
    tr[p].r = tr[q].l;
    tr[q].l = p;
    p = q;
    pushup(tr[p].l);
    pushup(p);
}
void insert(int &p, int key)
{
    if(!p) p = get_node(key);
    else if(tr[p].key == key) tr[p].cnt++;
    else if(tr[p].key > key)
    {
        insert(tr[p].l, key);
        if(tr[tr[p].l].val > tr[p].val) zig(p);
    }
    else
    {
        insert(tr[p].r, key);
        if(tr[tr[p].r].val > tr[p].val) zag(p);
    }
    pushup(p);
}
void remove(int &p, int key)
{
    if(!p) return;
    if(tr[p].key == key)
    {
        if(tr[p].cnt > 1) tr[p].cnt--;
        else if(tr[p].l || tr[p].r)
        {
            if(!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val)
            {
                zig(p);
                remove(tr[p].r, key);
            }
            else
            {
                zag(p);
                remove(tr[p].l, key);
            }
        }
        else p = 0;
    }
    else if(tr[p].key > key) remove(tr[p].l, key);
    else remove(tr[p].r, key);
    pushup(p);
}
int get_rank_by_key(int &p, int key)
{
    if(!p) return 1;
    if(tr[p].key == key) return tr[tr[p].l].siz + 1;
    if(tr[p].key > key) return get_rank_by_key(tr[p].l, key);
    return tr[tr[p].l].siz + tr[p].cnt + get_rank_by_key(tr[p].r, key);
}
int get_key_by_rank(int &p, int rank)
{
    if(!p) return INF;
    if(tr[tr[p].l].siz >= rank) return get_key_by_rank(tr[p].l, rank);
    if(tr[tr[p].l].siz + tr[p].cnt >= rank) return tr[p].key;
    return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].siz - tr[p].cnt);
}
int get_prev(int p, int key)
{
    if(!p) return -INF;
    if(tr[p].key >= key) return get_prev(tr[p].l, key);
    return max(tr[p].key, get_prev(tr[p].r, key));
}
int get_next(int p, int key)
{
    if(!p) return INF;
    if(tr[p].key <= key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}

int main()
{
    build();
    cin >> n;
    while(n--)
    {
        int op, x;
        scanf("%d%d", &op, &x);
        if(op == 1) insert(root, x);
        else if(op == 2) remove(root, x);
        else if(op == 3) printf("%d\n", get_rank_by_key(root, x) - 1); // 哨兵
        else if(op == 4) printf("%d\n", get_key_by_rank(root, x + 1));
        else if(op == 5) printf("%d\n", get_prev(root, x));
        else if(op == 6) printf("%d\n", get_next(root, x));
    }
    return 0;
}

/* ???
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
vector<int> a;
int qread(){
    int fx=0; 
    char ch=getchar();
    while(ch<'0' || ch>'9') ch=getchar();
    while(ch>='0' && ch<='9'){
        fx=fx*10+ch-'0';
        ch=getchar();
    }
    return fx;
}
int main()
{
    int n,opt,x;
    scanf("%d",&n);
    a.reserve(100005);
    while(n--)
    {
        scanf("%d%d",&opt,&x);
        switch(opt)
        {
            case 1:a.insert(upper_bound(a.begin(),a.end(),x),x); break;
            case 2:a.erase(lower_bound(a.begin(),a.end(),x)); break;
            case 3:cout<<lower_bound(a.begin(),a.end(),x)-a.begin()+1<<endl; break;
            case 4:cout<<a[x-1]<<endl; break;
            case 5:cout<<(*--lower_bound(a.begin(),a.end(),x))<<endl; break;
            case 6:cout<<(*upper_bound(a.begin(),a.end(),x))<<endl; break;
        }
    }
    return 0;
}
*/

AcWing256

在一堆数中找到和某个数最接近的数。

可以分成两种情况：前驱和后继。

所以操作就有：

  1. 插入
  2. 找前驱（lower_bound）/后继（upper_bound--）

所有 set 能做的平衡树都可以做，平衡树可以多维护几个值，而 set 不行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <bits/stdc++.h>
using namespace std;
const int N = 33300;
const int INF = 1e8;
typedef long long LL;

int n;
struct Node
{
    int l, r;
    int key, val;
}tr[N];

int root, idx;

int get_node(int key)
{
    tr[++idx].key = key;
    tr[idx].val = rand();
    return idx;
}
void build()
{
    get_node(-INF);
    get_node(INF);
    root = 1;
    tr[1].r = 2;
}
void zig(int &p)
{
    int q = tr[p].l;
    tr[p].l = tr[q].r;
    tr[q].r = p;
    p = q;
}
void zag(int &p)
{
    int q = tr[p].r;
    tr[p].r = tr[q].l;
    tr[q].l = p;
    p = q;
}
void insert(int &p, int key)
{
    if(!p) p = get_node(key);
    else if(tr[p].key == key) return;
    else if(tr[p].key > key)
    {
        insert(tr[p].l, key);
        if(tr[tr[p].l].val > tr[p].val) zig(p);
    }
    else
    {
        insert(tr[p].r, key);
        if(tr[tr[p].r].val > tr[p].val) zag(p);
    }
}
int get_prev(int p, int key)
{
    if(!p) return -INF;
    if(tr[p].key > key) return get_prev(tr[p].l, key);
    return max(tr[p].key, get_prev(tr[p].r, key));
}
int get_next(int p, int key)
{
    if(!p) return INF;
    if(tr[p].key < key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}

int main()
{
    build();
    cin >> n;
    LL res = 0;
    for(int i = 1; i <= n; i++)
    {
        int x;
        scanf("%d", &x);
        if(i == 1) res += x;
        else res += min(x - get_prev(root, x), get_next(root, x) - x);
        insert(root, x);
    }
    printf("%lld\n", res);
    return 0;
}

删除

把对应节点旋转到叶子节点后删除即可。

FHQ Treap

非旋转 Treap，通过分裂和合并来维护。
参考文章

Split

一旦优先级确定，并且一个单调递增的序列确定，那么这个区间怎样分裂和合并对这颗树的结构是没有影响的。

所以我们把整个区间分为左区间和右区间，相当于切了一刀。

一开始先创建两个虚拟点，然后从原二叉搜索树中的根节点开始遍历，假如当前节点的 valnowval_{now} 小于等于划分的边界的 valval，那么当前节点以及它的子树都应该属于左区间，此时应该将左区间的虚拟点的指针指向当前节点，虚拟节点由虚变实，然后以当前节点的右儿子为下一个虚拟点继续递归，因为 ≤valnow\le val_{now} 的都已经在左区间了，我们还要找的是 valnow<x≤valval_{now} < x\le val 的节点。

假如当前节点的 valnowval_{now} 大于划分的边界 valval 的话，那么我们就应该把当前节点以及它的右子树给划分到右区间中，并将虚拟点的指针指向当前节点，把当前节点的左儿子变为下一个虚拟点继续递归。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void split(int now, int k, int &x, int &y) // x y 代表的是当前递归的是左区间还是右区间的节点
{
    if(!now)
    {
        x = y = 0;
        return;
    }
    if(tr[now].val <= k)
    {
        x = now;
        split(tr[now].r, k, tr[now].r, y); // 左区间的当前点的右儿子
    }
    else
    {
        y = now;
        split(tr[now].l, k, x, tr[now].l); // 右区间的当前点的左儿子
    }
    pushup(now);
}
...
split(root, q, x, y); // 分裂后 x 得到的就是左区间的根节点，y 就是右区间的根节点。

Merge

Splay

其它

  • STL map
  • 红黑树（巨麻烦）
  • SBT
  • AVL

可持久化

数据结构可以进行可持久化的前提是本身的拓扑结构不变，变的只是里面的数据。

比如：线段树、树状数组、Trie 树、堆、并查集。

可以把所有的修改的历史版本记录下来。

如果全部备份的话，那么消耗会非常的大。

只需要记录每一个版本相对于前一个版本变化的地方。

比如线段树，每次操作最多需要记录 log 级别的节点，把复杂度从平方变成 log。

[[字符串#可持久化 Trie 树|可持久化 Trie 树]]

[[数据结构#可持久化线段树|可持久化线段树]]

树链剖分

可以通过给树中的点编号，使得可以将书中任意一条路径变成链的序列里 lognlogn 段连续的区间。

就可以把树上问题转化为区间问题。

转换为区间后，用数据结构就可以维护了。

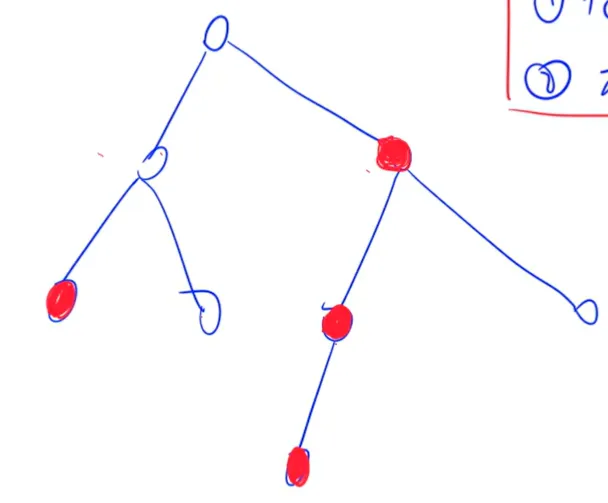
  1. 重儿子/轻儿子（叶子节点没有），重儿子为子树大小最大的儿子，若多个都是最大，那么就任选一个，其它都是轻儿子。

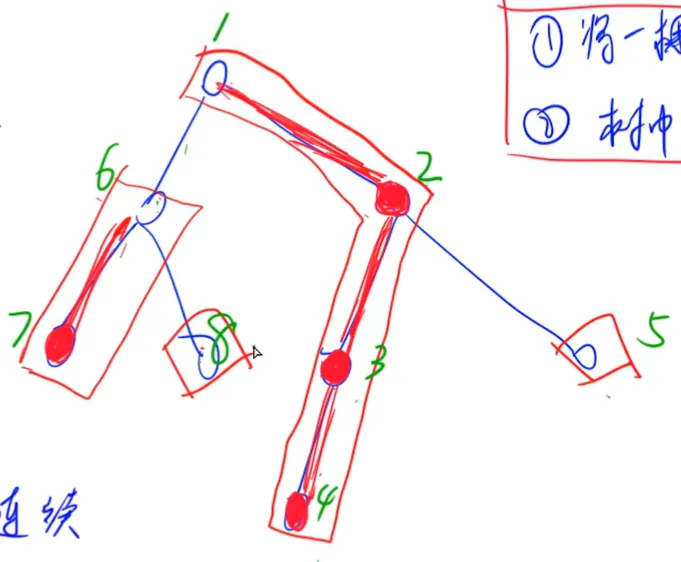
image.png|300

  1. 重/轻边：重儿子和它父亲之间的边叫做重边，其余的叫做轻边。
  2. 重/轻链：重边组成重链，落单的节点也叫做重链，重儿子所在的重链为它父亲所在的重链，轻儿子所在的重链为它重儿子所在的重链。

按照 DFS 序（优先遍历重儿子，这样重链的编号都是连续的，顺便求一下子树大小）把整个树变成一个区间。

image.png|300

定理：树中任意一条路径均可拆分成 O(logn)O(logn) 条重链（即连续区间）。

标记一下每个点所在重链的顶点即可。

那么如何把路径用区间表示呢？

可以用类似最近公共祖先的方法，每次取深度较深的重链，让它向上走，直到走到同一条重链（最近公共祖先所在的重链），这样就可以分为 lognlogn 条链（也就是区间），这样就可以对区间进行操作，总复杂度在 log2nlog^2n 的级别内。

并且可以注意到重链的顶点一定是某一个轻儿子。

A2568

  1. 区间修改
  2. 区间修改（因为子树里的点 DFS 编号是连续的）
  3. 区间查询
  4. 区间查询
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 7;
const int M = N << 1;

int n, m;
struct Edge
{
    int nxt, to;
}e[M];
int fir[N];
int w[N];
int id[N], nw[N], cnt, idx;
int dep[N], sz[N], top[N], fa[N], son[N]; // 深度，子树大小，重链顶点，父节点，儿子节点
struct Node
{
    int l, r;
    LL sum, add;
}tr[N << 2];

void add(int u, int v)
{
    e[++idx].nxt = fir[u];
    e[idx].to = v;
    fir[u] = idx;
}
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{
    Node &root = tr[u], &left = tr[u << 1], &righ = tr[u << 1 | 1];
    if(root.add)
    {
        left.add += root.add;
        righ.add += root.add;
        left.sum += (left.r - left.l + 1) * root.add;
        righ.sum += (righ.r - righ.l + 1) * root.add;
        root.add = 0;
    }
}
void build(int u, int l, int r)
{
    tr[u].l = l, tr[u].r = r;
    if(l == r)
    {
        tr[u].sum = nw[r];
        return;
    }
    int mid = (l + r) >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
}
void update(int u, int l, int r, int k)
{
    if(l <= tr[u].l && tr[u].r <= r)
    {
        tr[u].add += k;
        tr[u].sum += k * (tr[u].r - tr[u].l + 1);
        return;
    }
    pushdown(u);
    int mid = (tr[u].l + tr[u].r) >> 1;
    if(l <= mid) update(u << 1, l, r, k);
    if(r > mid) update(u << 1 | 1, l, r, k);
    pushup(u);
}
LL query(int u, int l, int r)
{
    if(l <= tr[u].l && tr[u].r <= r) return tr[u].sum;
    pushdown(u);
    int mid = (tr[u].l + tr[u].r) >> 1;
    LL res = 0;
    if(l <= mid) res += query(u << 1, l, r);
    if(r > mid) res += query(u << 1 | 1, l, r);
    return res;
}
void dfs1(int u, int fath, int depth)
{
    dep[u] = depth, fa[u] = fath;
    sz[u] = 1; // important
    for(int i = fir[u]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        if(v == fath) continue;
        dfs1(v, u, depth + 1);
        sz[u] += sz[v];
        if(sz[son[u]] < sz[v]) son[u] = v;
    }
}
void dfs2(int u, int t)
{
    id[u] = ++cnt;
    nw[cnt] = w[u]; // 方便线段树的维护
    top[u] = t;
    if(!son[u]) return;
    dfs2(son[u], t);
    for(int i = fir[u]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        if(v == fa[u] || v == son[u]) continue;
        dfs2(v, v);
    }
}
void update_path(int u, int v, int k)
{
    while(top[u] != top[v]) // 不在同一条重链里
    {
        if(dep[top[u]] < dep[top[v]]) swap(u, v); // 保证 u 所在重链较深
        update(1, id[top[u]], id[u], k);
        u = fa[top[u]];
    }
    if(dep[u] < dep[v]) swap(u, v); // u 深度更大
    update(1, id[v], id[u], k); // 在同一条重链里
}
LL query_path(int u, int v)
{
    LL res = 0;
    while(top[u] != top[v])
    {
        if(dep[top[u]] < dep[top[v]]) swap(u, v);
        res += query(1, id[top[u]], id[u]);
        u = fa[top[u]];
    }
    if(dep[u] < dep[v]) swap(u, v);
    res += query(1, id[v], id[u]);
    return res;
}
void update_tree(int u, int k)
{
    update(1, id[u], id[u] + sz[u] - 1, k); // 子树是一段连续的区间
}
LL query_tree(int u)
{
    return query(1, id[u], id[u] + sz[u] - 1);
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &w[i]);
    for(int i = 1; i < n; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        add(b, a);
    }
    dfs1(1, -1, 1); // 点的编号 父节点 深度
    dfs2(1, 1); // 当前点 重链的顶点 
    build(1, 1, n);
    scanf("%d", &m);
    while(m--)
    {
        int t, u, v, k;
        scanf("%d%d", &t, &u);
        switch(t)
        {
            case 1:
                scanf("%d%d", &v, &k);
                update_path(u, v, k);
                break;
            case 2:
                scanf("%d", &k);
                update_tree(u, k);
                break;
            case 3:
                scanf("%d", &v);
                printf("%lld\n", query_path(u, v));
                break;
            case 4:
                printf("%lld\n", query_tree(u));
                break;
        }
    }
    return 0;
}

A918

A 依赖 B，每个软件有且只有一个依赖软件，安装 A 之前必须安装 B，卸载 B 之前必须先卸载 A。

每个点只有两个状态：已安装/未安装。

操作：

  • 安装 x：把根到 x 路径上的所有点变成 1
  • 卸载 x：把以 x 为根的子树全部变成 0

询问：

操作了多少个节点，维护一下总的区间和，作差即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 7;

int n, m, cnt, idx;
int fir[N];
int dep[N], sz[N], top[N], fa[N], son[N], id[N];
struct Edge
{
    int nxt, to;
}e[N];
struct Node
{
    int l, r;
    // -1:ÎÞ²Ù×÷ 0:°Ñ½ÚµãËùÓÐÖµ±ä³É0 1:°Ñ½ÚµãËùÓÐÖµ±äΪ1
    int add, sum;
}tr[N << 2];

void add(int u, int v)
{
    e[++cnt].nxt = fir[u];
    e[cnt].to = v;
    fir[u] = cnt;
}
void dfs1(int u, int depth)
{
    dep[u] = depth, sz[u] = 1;
    for(int i = fir[u]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        dfs1(v, depth + 1);
        sz[u] += sz[v];
        if(sz[son[u]] < sz[v]) son[u] = v;
    }
}
void dfs2(int u, int t)
{
    id[u] = ++idx;
    top[u] = t;
    if(!son[u]) return;
    dfs2(son[u], t);
    for(int i = fir[u]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        if(v == son[u]) continue;
        dfs2(v, v);
    }
}
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{
    Node &root = tr[u], &left = tr[u << 1], &righ = tr[u << 1 | 1];
    if(root.add != -1)
    {
        left.add = righ.add = root.add;
        left.sum = (left.r - left.l + 1) * root.add;
        righ.sum = (righ.r - righ.l + 1) * root.add;
        root.add = -1;
    }
}
void build(int u, int l, int r)
{
    tr[u].l = l, tr[u].r = r, tr[u].add = -1, tr[u].sum = 0;
    if(l == r) return;
    int mid = (l + r) >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
void update(int u, int l, int r, int k)
{
    if(l <= tr[u].l && tr[u].r <= r)
    {
        tr[u].add = k;
        tr[u].sum = k * (tr[u].r - tr[u].l + 1);
        return;
    }
    pushdown(u);
    int mid = (tr[u].l + tr[u].r) >> 1;
    if(l <= mid) update(u << 1, l, r, k);
    if(r > mid) update(u << 1 | 1, l, r, k);
    pushup(u);
}
void update_path(int u, int v, int k)
{
    while(top[u] != top[v])
    {
        if(dep[top[u]] < dep[top[v]]) swap(u, v);
        update(1, id[top[u]], id[u], k);
        u = fa[top[u]];
    }
    if(dep[u] < dep[v]) swap(u, v);
    update(1, id[v], id[u], k);
}
void update_tree(int u, int k)
{
    update(1, id[u], id[u] + sz[u] - 1, k);
}

int main()
{
    scanf("%d", &n);
    for(int i = 2; i <= n; i++)
    {
        int p;
        scanf("%d", &p);
        p++;
        add(p, i);
        fa[i] = p;
    }
    dfs1(1, 1);
    dfs2(1, 1);
    build(1, 1, n);
    scanf("%d", &m);
    int u;
    char op[10];
    while(m--)
    {
        scanf("%s%d", op, &u);
        u++;
        if(!strcmp(op, "install"))
        {
            int t = tr[1].sum;
            update_path(1, u, 1);
            printf("%d\n", tr[1].sum - t);
        }
        else
        {
            int t = tr[1].sum;
            update_tree(u, 0);
            printf("%d\n", t - tr[1].sum);
        }
    }
    return 0;
}
g
  • Title: 数据结构
  • Author: Falling_Sakura
  • Created at : 2023-06-23 19:16:50
  • Updated at : 2025-09-25 10:18:02
  • Link: https://vercel.fallingsakura.top/668ad1af.html
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
数据结构
  1. 1. 前言
  2. 2. 链表
    1. 2.1. 动态链表
    2. 2.2. 静态链表
      1. 2.2.1. 手写静态链表:
  3. 3. 队列
    1. 3.1. 手写队列
  4. 4. 双端队列和单调队列
    1. 4.1. DP优化
  5. 5. 栈
    1. 5.1. 单调栈
  6. 6. STL
    1. 6.1. Vector
      1. 6.1.1. 初始化
      2. 6.1.2. 添加元素
      3. 6.1.3. 插入元素
      4. 6.1.4. 删除元素
    2. 6.2. Map
      1. 6.2.1. 定义：
      2. 6.2.2. 使用：
      3. 6.2.3. 删除与清空：
      4. 6.2.4. 大小
    3. 6.3. Unordered_map
    4. 6.4. Queue
    5. 6.5. List
    6. 6.6. Priority_queue
    7. 6.7. Stack
    8. 6.8. Bitset
    9. 6.9. Multiset
    10. 6.10. Set
  7. 7. 二叉树
    1. 7.1. 遍历
      1. 7.1.1. 广度优先遍历(BFS)
      2. 7.1.2. 深度优先遍历(DFS)
    2. 7.2. 哈夫曼树
  8. 8. 堆
    1. 8.1. 手写堆
    2. 8.2. 练习
  9. 9. 并查集
  10. 10. 线段树
    1. 10.1. 建树
    2. 10.2. 查询
    3. 10.3. 单点修改
    4. 10.4. 懒标记
      1. 10.4.1. 区间加法
      2. 10.4.2. 区间乘法
    5. 10.5. 扫描线法
    6. 10.6. 动态开点
    7. 10.7. 可持久化线段树
    8. 10.8. 习题
  11. 11. 树状数组
    1. 11.1. Lowbit函数
    2. 11.2. 习题
  12. 12. 平衡树
    1. 12.1. Treap
      1. 12.1.1. BST
      2. 12.1.2. 插入
      3. 12.1.3. 旋转
      4. 12.1.4. 删除
    2. 12.2. FHQ Treap
      1. 12.2.1. Split
      2. 12.2.2. Merge
    3. 12.3. Splay
    4. 12.4. 其它
  13. 13. 可持久化
    1. 13.1. [[字符串#可持久化 Trie 树|可持久化 Trie 树]]
    2. 13.2. [[数据结构#可持久化线段树|可持久化线段树]]
  14. 14. 树链剖分